Локальная блочная элиминация для задачи дискретной оптимизации с ограничениями

Пример 8.3.Рассмотрим задачу ДО из примера 8.1 и упорядоченное раз­бие­ние множества переменных 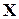на блоки: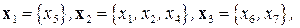 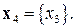Для упорядоченного разбиения 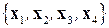данная задача ДО с огра­ни­чениями может быть решена с помощью ЛЭА.

A. Прямая часть

Рассмотрим вначале блок 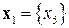. Для него 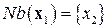. Решим следу­ющую задачу оптимизации, содержащую 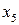в целевой функции и ограни­чени­ях:

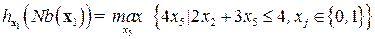
и сохраним оптимальные локальные решения 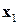в виде функции переменных окрестности: 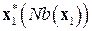в таблице 8.13. Элиминируем блок 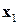и рассмотрим блок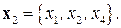 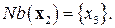Для решения осталась следующая задача:

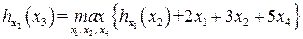
при ограничениях

,

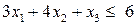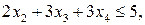
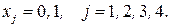
Построим соответствующую таблицу 8.14. Элиминируем блок 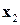и рассмотрим блок 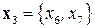. Соседней к 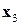является вершина 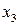: 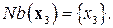Решим задачу ДО, содержащую :

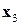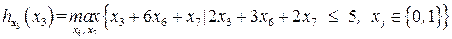
и построим таблицу 8.15.

Таблица 8.15. Вычисление .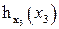

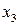
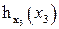
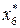
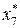
Элиминируем блок 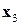и рассмотрим блок 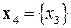. 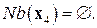Решим задачу ДО 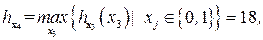где .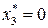

B. Обратная часть

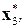
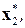
Последовательно найдем 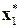‑ оптимальные локальные решения из сохраненных таблиц 8.15, 8.14, 8.13.

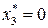
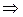
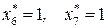(таблица 8.15);

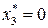
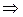
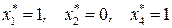(таблица 8.14);

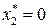
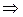
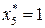(таблица 8.13).

Итак, найдено оптимальное глобальное решение (1, 0, 0, 1, 1, 1, 1), при этом максимальное значение целевой функции равно 18.

8.3.7. Локальные алгоритмы, использующие древовидную структурную декомпозицию.

Рассмотрим ЛА для решения задач ДО с древовидной струк­турой, т.е. для которых известна ДД, которую мы считаем заданной в виде множества блоков переменных и ограничений и соответствующего дерева 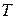, описывающего связь блоков. Отметим, что рассмотренная выше блочно-древовидная структура является частным случаем древовидной декомпозиции. Пусть 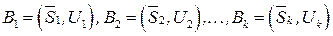‑ блоки ДД, где 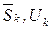являются соответственно множествами индексов переменных и ограничений для 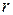-го блока, 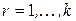, причем

, ,

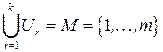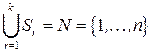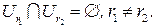
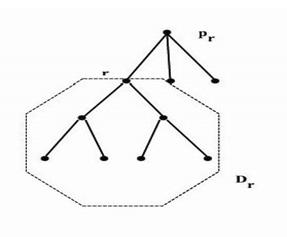
Рассмотрим дерево 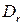, состоящее из вер­ши­ны 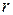дерева 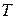и всех ее потомков. Работа ЛА A_BT для решения задач ДО с древовидной структурой основана именно на том, что при фиксации вектора 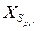задача распадается на 2 задачи: первая соответствует дереву 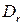; а вторая ‑ дереву .

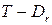Введем необходимые обозначения:

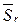‑ множество индексов переменных, принадлежащих блоку ;

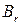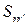‑ множество индексов переменных, принадлежащих одновременно блокам 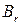и 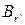, т.е. ;

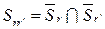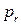‑ вершина-предок вершины ;

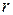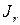‑ множество потомков вершины .

Рис. 8.10. Дерево потомков.

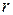Тогда 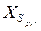‑ вектор переменных, общих для блоков 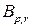и 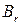(здесь .

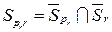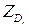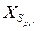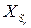Обозначим через следующую задачу: для каждого вектора найти и 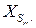, такие, что

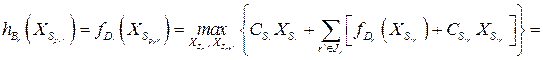
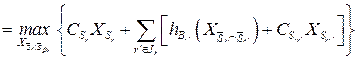
при ограничениях

.

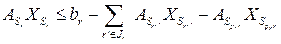Здесь 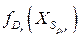‑ значение целевой функции задачи, соответствующей дереву 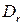, 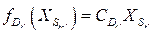. Можно это значение приписать корню 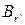дерева 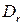, т.е. записать: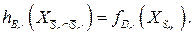

ЛА решает задачи ДО 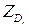, двигаясь снизу вверх, от листьев ДД к корню дерева .

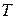Обсудим возможности применения релаксаций в вычислительной процедуре ЛЭА. При решении задачи 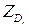целесообразно решать вспомогательные задачи ДО следующего вида:

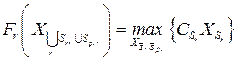
при ограничениях

.

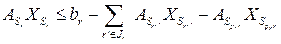При решении задачи 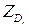можно использовать вместо значений целевой функции 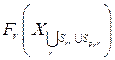значения целевых функций их релаксированных задач (например, линейной релаксации, когда вместо задачи ДО рассматривается соответствующая задача линейного программирования; ранцевой релаксации, в которой вместо ограничений исходной задачи рассматривается суррогатное ограничение, являющееся линейной комбинацией исходных ограничений и т.д.).

Алгоритмы выделения блочно-древовидных структур в разреженных графах взаимосвязей дискретных задач, позволяющих применение локальных элиминационных алгоритмов для решения этих задач.