Локальные элиминационные алгоритмы в задачах дискретной оптимизации
Рассмотрим задачу ДО с ограничениями
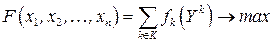 (8.8)
(8.8)
при ограничениях
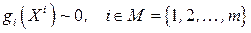 , (8.9)
, (8.9)
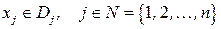 , (8.10)
, (8.10)
где 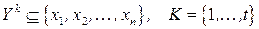 ,
, 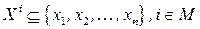 ; ~ – одно из отношений
; ~ – одно из отношений 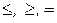 ,
, 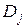 – конечное множество возможных значений переменной
– конечное множество возможных значений переменной 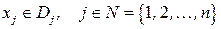 .
.  Функции
Функции 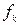
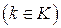 называются компонентами целевой функции.
называются компонентами целевой функции.
Пример 8.1. Найти максимум функции с бинарными переменными:
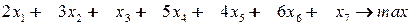 (8.11)
(8.11)
при ограничениях

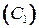 (8.12)
(8.12)
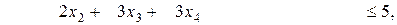
 (8.13)
(8.13)

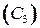 (8.14)
(8.14)

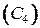 (8.15)
(8.15)
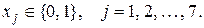
8.3.3. Задание структуры разреженных задач дискретной оптимизации с помошью графового и гиперграфового представлений
Элементный граф
Рассмотрим подробнее детали реализации ЛЭА при решении задач ДО в случае, когда структурный граф является графом взаимосвязейпеременных, который в литературе называется также графом ограничений [33]. В графе взаимосвязей задачи ДО вершины соответствуют переменным, причем две вершины соединяются ребром, если соответствующие переменные имеются в одном и том же ограничении.
Определение 8.3. Две переменные 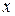 и
и 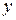 взаимосвязаны в задаче ДО с ограничениями, если они появляются вместе в одном компоненте ЦФ или в одном и том же ограничении (другими словами, если переменные
взаимосвязаны в задаче ДО с ограничениями, если они появляются вместе в одном компоненте ЦФ или в одном и том же ограничении (другими словами, если переменные 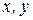 входят одновременно во множество
входят одновременно во множество 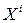 или во множество
или во множество 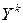 .
.
Определение 8.4. Графом взаимосвязей задачи ДО называется неориентированный граф 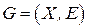 , для которого
, для которого
· множество вершин 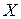 соответствует множеству переменных
соответствует множеству переменных 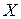 задачи ДО;
задачи ДО;
· две вершины графа соединены ребром тогда и только тогда, когда соответствующие им переменные взаимосвязаны.
В дальнейшем будем отождествлять переменные задачи ДО с вершинами графа взаимосвязей.
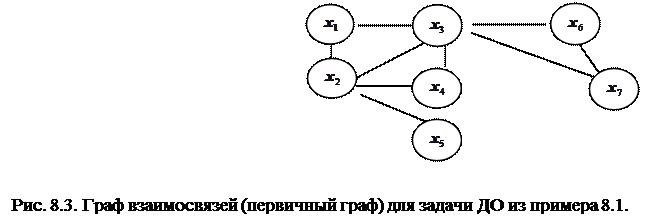 |
Основным понятием в теории локальных алгоритмов является понятие близости элементов, определяемое понятием окрестности.
Определение 8.5. Две вершины 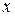 и
и 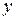 в графе
в графе 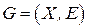 называются соседними, если
называются соседними, если 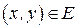 .
.
Определение 8.6. Множество переменных, соседних с переменной 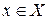 в графе
в графе 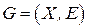 , обозначается
, обозначается 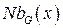 (или
(или 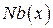 ) и называется окрестностью переменной
) и называется окрестностью переменной 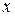 .
.
Дата добавления: 2016-06-05; просмотров: 1483;











