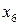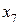Локальная блочная элиминация для задачи дискретной оптимизации без ограничений
Пример 8.2. Рассмотрим в качестве примера задачу ДО без ограничений
|
|
|
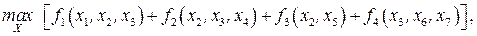 где
где 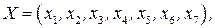 а функции
а функции 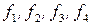 заданы таблицами.
заданы таблицами.
|
Рассмотрим упорядоченное разбиение множества переменных  на блоки:
на блоки: 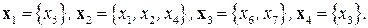 Граф взаимосвязей задачи показан на рис. 8.3.
Граф взаимосвязей задачи показан на рис. 8.3.
Для упорядоченного разбиения 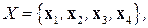 эта задача ДО без ограничений может быть решена с помощью ЛЭА. Исходный граф взаимосвязей с разбиением, представленным пунктиром, показан на рис. 8.8 (a), фактор-граф взаимосвязей – на рис. 8.8 (b), и бесконтурный орграф вычислительной процедуры локального блочного элиминационного алгоритма приведен на рис. 8.9.
эта задача ДО без ограничений может быть решена с помощью ЛЭА. Исходный граф взаимосвязей с разбиением, представленным пунктиром, показан на рис. 8.8 (a), фактор-граф взаимосвязей – на рис. 8.8 (b), и бесконтурный орграф вычислительной процедуры локального блочного элиминационного алгоритма приведен на рис. 8.9.
 Рис. 8.8. Граф взаимосвязей задачи ДО с разбиением, выделенным пунктиром (a) и фактор-граф взаимосвязей (b) (пример 8.2).
Рис. 8.8. Граф взаимосвязей задачи ДО с разбиением, выделенным пунктиром (a) и фактор-граф взаимосвязей (b) (пример 8.2).
 Рис. 8.9. Бесконтурный орграф (обобщенное элиминационное дерево) локальной блочной элиминационной вычислительной процедуры для задачи ДО (пример 8.2).
Рис. 8.9. Бесконтурный орграф (обобщенное элиминационное дерево) локальной блочной элиминационной вычислительной процедуры для задачи ДО (пример 8.2).
A. Прямая часть.Рассмотрим вначале блок 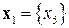 . Тогда
. Тогда 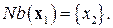 Решим с помощью полного перебора следующую задачу оптимизации
Решим с помощью полного перебора следующую задачу оптимизации
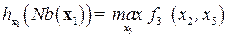
и запомним оптимальные локальные решения 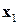 как функцию переменных из окрестности, т.е.
как функцию переменных из окрестности, т.е. 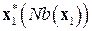 .
.
Исключим блок 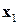 и рассмотрим блок
и рассмотрим блок 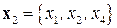 .
. 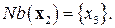 Нужно решить далее задачу
Нужно решить далее задачу
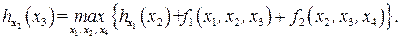

 Построим соответствующую таблицу 8.11.
Построим соответствующую таблицу 8.11.
Элиминируем блок 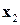 и рассмотрим блок
и рассмотрим блок 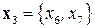 . Соседней к
. Соседней к 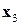 является вершина
является вершина 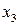 :
: 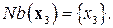 Решим задачу ДО, содержащую
Решим задачу ДО, содержащую 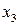 :
:
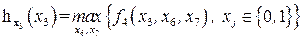 и построим таблицу 8.12.
и построим таблицу 8.12.
Таблица 8.12. Вычисление 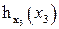 .
.
| 
| 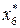
| 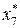
|
Элиминируем блок 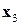 и рассмотрим блок
и рассмотрим блок 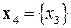 .
. 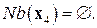 Решим задачу ДО
Решим задачу ДО 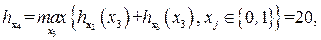 где
где 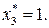
B. Обратная часть.Последовательно найдем 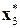 ,
, 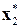 ,
, 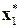 , т.е. оптимальные локальные решения из сохраненных таблиц 8.12, 8.11, 8.10:
, т.е. оптимальные локальные решения из сохраненных таблиц 8.12, 8.11, 8.10: 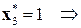
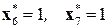 (таблица 8.12);
(таблица 8.12); 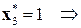
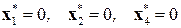 (таблица 8.11);
(таблица 8.11); 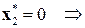
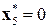 (таблица 8.10). В результате найдено оптимальное решение (0, 0, 1, 0, 0, 1, 1), максимальное значение целевой функции равно 20.
(таблица 8.10). В результате найдено оптимальное решение (0, 0, 1, 0, 0, 1, 1), максимальное значение целевой функции равно 20.
Дата добавления: 2016-06-05; просмотров: 1639;

 .
.
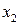
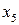
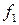 .
.
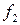
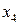
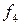 .
.