Определение уравнения регрессии второго порядка.

Для определения параметров эмпирической зависимости, выраженной уравнением регрессии второго порядка в виде

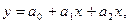
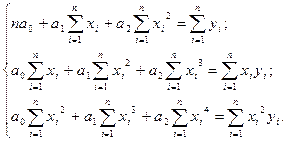необходимо составить систему уравнений:

(2.9)

Суммы, входящие в систему (2.9), удобно вычислять в программе MS EXCEL, пользуясь схемой (рисунок 2.3).

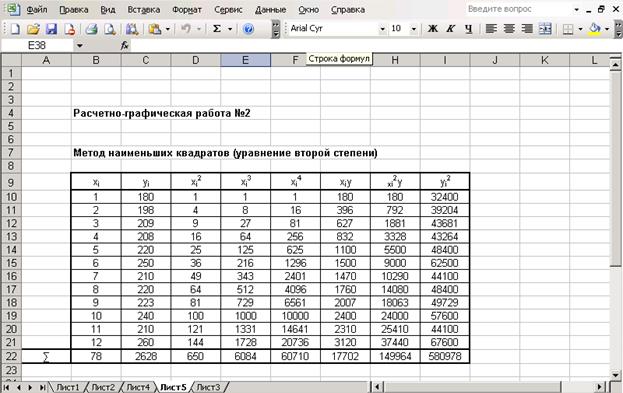
Рис.2.3. Расчет параметров уравнения 2-ой степени по методу наименьших квадратов.

Определив суммы, входящие в систему уравнений, получим:

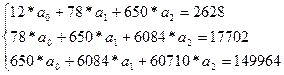
Далее решаем систему уравнений MS EXCEL

Решение будет заключаться в умножении обратной матрицы коэффициентов при неизвестных на матрицу свободных членов. Эти операции можно выполнить последовательно, т.е. сначала определить обратную матрицу коэффициентов при неизвестных при помощи функции МОБР, а затем полученную обратную матрицу умножить на матрицу свободных членов, при помощи функции МУМНОЖ, в диалоговом окне которой вызывается встроенная функция у первого массива, где в свою очередь вызывается функция обращения и вводится матрица коэффициентов. Для второго массива диалогового окна функции МУМНОЖ вводится диапазон матрицы свободных членов. Ввод заканчивается комбинацией клавиш <Shift>+<Ctrl>+<Enter>. Например для нашего случая (рис.2.4.), матрица коэффициентов записана в диапазоне С27:Е29, а матрица свободных членов- в диапазоне Н27:Н29, формула выглядит следующим образом:

{=МУМНОЖ(МОБР(С27:Е29);Н27:Н29)}

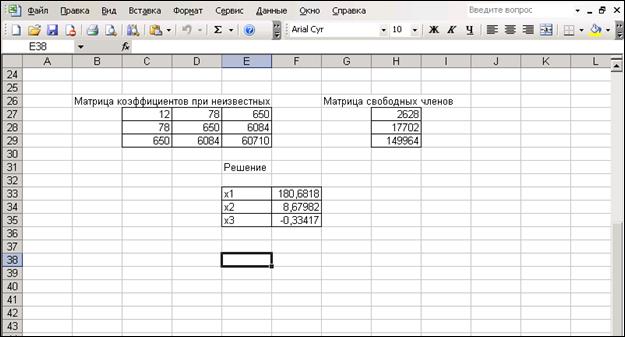
Рис.2.4. Решение системы линейных уравнений.

В результате уравнение регрессии второго порядка имеет следующий вид:

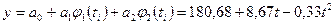
Определяем прогноз на 13 месяц:

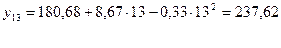
Погрешность определяется так же, как для уравнения первой степени.

2.2.2. Применение метода Чебышева для прогнозирования спроса.

Для построения многочлена воспользуемся вспомогательной таблицей (табл.2.3.), выполненной в MS Excel:

Таблица 2.3.

Промежуточные вычисления для построения многочлена и определения погрешностей по методу Чебышева.

Построение многочлена первой степени.

Согласно (2.10)

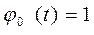
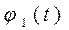
Находим многочлен по формуле (2. 18)

.

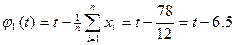Согласно (2.17)

.

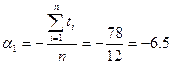По формуле (2.14) находим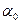

.

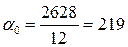Уравнение 0 степени будет равно:

y = .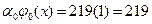

Найдем а₁ по формуле (2.14)

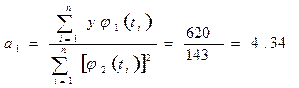
где:

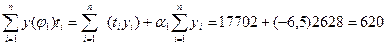
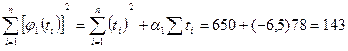
Многочлен первой степени будет равен:

.

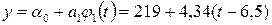Окончательно

y=219 + 4,34t - 28,21 = 4,34t + 190,79.

Пользуясь полученным уравнением, определяем в следующем (13) месяце:

.

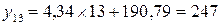Если точность результатов по этой формуле достаточна, обработка на этом может быть закончена.