ПРОГНОЗИРОВАНИЕ РАЗВИТИЯ МАТЕРИАЛОПОТОКА ЛЕСОПРОМЫШЛЕННОГО ПРЕДПРИЯТИЯ

Цель работы. Освоить традиционные и компьютерные методы статистического анализа производственно-хозяйственной деятельности лесопромышленного предприятия и методы прогнозирования деятельности на тактическом уровне.

Задача. Выполнить анализ деятельности лесопромышленного предприятия за предыдущий период и обосновать план производства на первые три месяца следующего периода с вероятностью 0,95 и 0, 98.

В лесопромышленной логистике основной целью является создание такой товаропроизводящей и товаропроводящей логистической системы, чтобы при минимально возможных затратах достичь максимально возможного эффекта.

Для создания эффективной логистической системы, в первую очередь, необходимо иметь возможность прогнозировать развитие потребностей и покупательной возможности потребителей, прогнозировать развитие своего производства и возможного развития конкурентов.

Прогнозирование дает возможность обосновать параметры проектирования новых лесозаготовительных и лесоперерабатывающих предприятий на предпроектной стадии, проектирования их реконструкции, а также совершенствования технологических процессов лесного производства.

Прогнозирование чаще всего производится с использованием экстраполяционных методов, которые базируются на предположении о том, что будущее является продолжением настоящего. При этом предполагается, что в будущем, в пределах прогноза, сохраняются существующие тенденции развития.

Прогнозирование производится с использованием математических методов, таких как метод наименьших квадратов, метод Чебышева, а в простейших случаях методов интерполирования, экспоненциального сглаживания, скользящей средней, экспертных оценок, имитационного моделирования и других.

Методы прогнозирования.Метод наименьших квадратов.Если известен вид эмпирической формулы y = f(x, a₀, a₁, .., a_m) и ее отклонения e_i = f(x_i, a₀, a₁, .., a_m) – y_i от исходных данных (x y_i). Согласно методу наименьших квадратов наилучшими коэффициентами a₀, a₁, .., a_m считаются те, для которых сумма квадратов отклонений минимальна, то есть

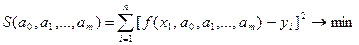(2.1)

Это возможно в том случае, если частные производные равны нулю:

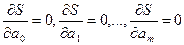(2.2)

Если эмпирическая формула f(x, a₀, a₁, .., a_m) линейна относительно ее параметров, то система (2.2) может быть представлена в простом виде. Полагая:

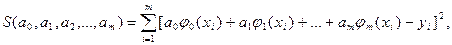получим

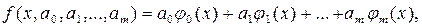отсюда

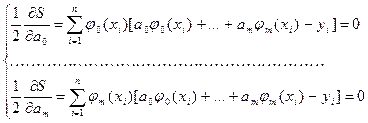(2.3)

В частности, если эмпирическая формула представляет собой полином

(2.4)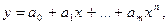

то после некоторых преобразований система (2.3) запишется в виде:

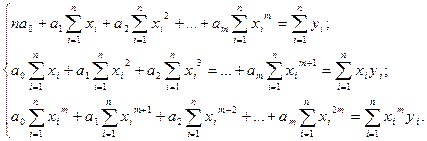(2.5)

Если уравнение регрессии представлено линейным уравнением вида

y = a₀ + a₁x, (2.6)

то параметры ее по методу наименьших квадратов находятся из системы уравнений:

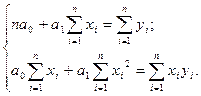(2.7)

Это система двух линейных уравнений с двумя неизвестными и имеет единственное решение. Схема нахождения сумм, входящих в систему (2.7), представлена в табл. 2.1.

Таблица 2.1.

Таблица для расчета параметров уравнения (2.7)

Номер Опыта	Значение параметра xi	Значение параметра yi	xiyi	xi2
	X1	y1	x1 y1	x12
	X2	y2	x2 y2	x22
…	…	…	…	…
n	xn	yn	xn yn	xn2

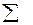
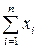
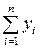
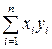
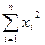
Для определения параметров эмпирической зависимости, выраженной уравнением регрессии второго порядка в виде

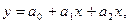(2.8)

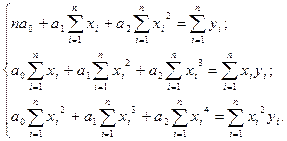необходимо составить систему уравнений:

(2.9)

Суммы, входящие в систему (2.9), удобно вычислять, пользуясь схемой табл. 2.2.

Таблица 2.2.

Таблица для расчета параметров уравнения (2.2)

Номер опыта	Значение параметра xi	Значение параметра yi	xi2	xi3	xi4	xiyi	xi2yi
	x1	y1	x12	x13	x14	x1y1	x12 y1
	x2	y2	x22	x23	x24	x2y2	x22 y2
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
.	.	.	.	.	.	.	.
n	xn	yn	xn2	xn3	xn4	xnyn	xn2yn

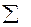
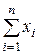
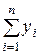
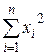
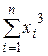
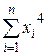
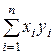
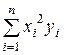
Решение систем уравнений (2.5), (2.7), (2.9) не представляет трудности, так как число уравнений равно числу неизвестных параметров. Недостатком метода является громоздкость вычислений.

2.1.1. Метод Чебышева.

Если в процессе обработки экспериментальных данных по методу наименьших квадратов возникает необходимость повысить степень многочлена, то требуется не только найти еще один коэффициент, но и пересчитать найденные ранее, так как изменяется система уравнений, из которой они определяются. В таком случае легче пользоваться методом Чебышева. Эмпирический многочлен ищется в виде суммы многочленов повышающихся степеней, причем добавление новых слагаемых не изменяет коэффициентов в предыдущих. Прибавляя член за членом, можно видеть, как убывает сумма квадратов отклонений величин, вычисленных по найденной формуле, от экспериментальных значений. При этом методе значительно облегчается выбор степени многочлена.

Пусть для n наблюдений требуется найти многочлен степени m с m+1 неизвестными коэффициентами a₀, a₁, …,a_m, при этом предполагается, что m<n.

Суть метода состоит в том, что эмпирический многочлен ищут не непосредственно в виде суммы степеней x, а в виде комбинаций много 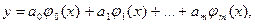членов, которые выбирают специальным образом. Запишем искомый многочлен в виде

(2.10)

где j₀(x) = 1, j₁(x) = x + a₁, … , j_m(x) = x + a_m,

Вообще j₁(x) – многочлен степени l имеет вид

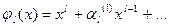(2.11)

со старшим коэффициентом, равным единице.

Предполагая, что многочлены каким-то образом выбраны, определим наиболее вероятные значения коэффициентов a₀, a₁, …,a_m. Находим способом наименьших квадратов минимум функции (2.1). При этом получим систему уравнений:

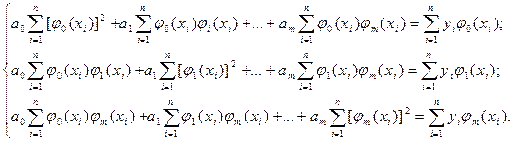(2.12)

Для упрощения системы (2.12) многочлены j₀(x),…, j_m(x) подбираются так, чтобы выполнить условия:

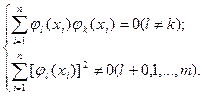
(2.13)

Это означает, что хотя бы в одной из точек x₁, x₂, …, x_n многочлен j_l(x) не равен нулю. Такие многочлены называются ортогональными многочленами Чебышева. При соблюдении указанных условий в левой части каждого уравнения (2.12) останется по одному числу, и тогда выражение для определения коэффициентов примет вид:

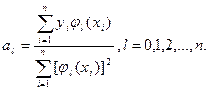(2.14)

Из условий (2.13), учитывая, что j₀(x) = 1 и приняв в них l = 0, k = 1 для многочлена j₁(x), получим:

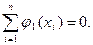(2.15)

Так как согласно формуле (2.11) многочлен

j₁(x) = x + a₁,

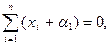то выражение (2.15) можно записать так:

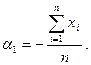(2.16)

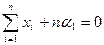откуда

или (2.17)

В результате

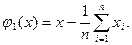(2.18)

Для построения многочлена j₂(x) положим в выражениях (2.13) последовательно l = 0, k = 2 и затем l = 1, k = 2, получим два уравнения:

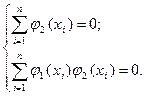(2.19)

j₂(x) – многочлен второй степени со старшим членом, равным единице. Поэтому его можно записать в виде

j₂(x) = (x + b₂)j₁(x) + g₂j₀(x). (2.20)

Подставив (2.20) в систему (2.19), и учитывая, что j₀(x) = 1, получим

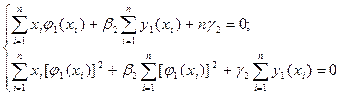
(2.21)

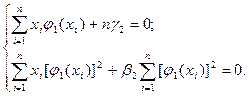или учитывая выражение (2.15)

(2.22)

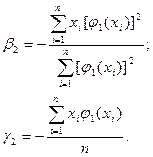Решая систему уравнений (2.22), получим:

(2.23)

Вычисляя коэффициенты b₂ и g₂, находим и многочлен j₂(x) по формуле (2.20).

При вычислении величин b₂ и g₂ по формулам (2.23) надо знать только суммы степеней

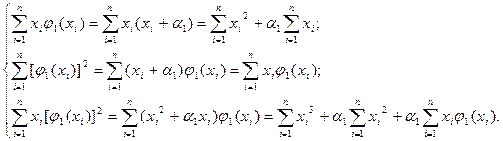
(2.24)

При выводах системы уравнений (2.24) учитывалось, что åj₁(x) = 0.

Таким образом, многочлены j₀(x), j₁(x), j₂(x) найдены. Теперь необходимо по формуле (2.14) установить наиболее вероятные значения коэффициентов a₀, a₁, …,a_m. Если многочлен (2.10) уже построен, то есть многочлены j₀(x),…, j_m(x) и коэффициенты a₀, …, a_m найдены, но точность многочлена нас не удовлетворяет, нужно найти следующий член a_m+1j_m+1(x). Для этого по формулам, аналогичным (2.20) и (2.22), строим многочлен j_m+1(x) и по формуле (2.24) находим коэффициент a_m+1.