Определение точности полученных зависимостей
| Месяц | Количество вагонов, факт. | Уравнение первой степени | Уравнение второй степени | ||||||
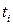
| 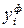
| 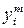
| 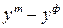
| 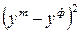
| 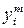
| 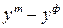
| 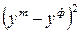
| ||
| -1 | |||||||||
| -5 | -5 | ||||||||
| -8 | -4 | ||||||||
| -33 | -29 | ||||||||
| -6 | -6 | ||||||||
| -17 | -22 | ||||||||
Среднее квадратическое отклонение
 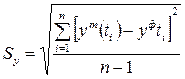
|
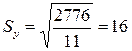
|
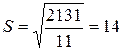
| |||||||
Принимая условие, что ошибка прогнозирования подчиняется нормальному закону распределения, можно считать, что с вероятностью 0,95 по правилу 2σ, спрос на продукцию в следующем месяце, приняв уравнение прогноза по закону линейной регрессии, находится в пределах 215 – 279.
Если за основу принять многочлен второй степени, то с такой же степенью вероятности, спрос на продукцию будет в пределах 209 – 265.
Для определения корреляционных зависимостей при прогнозировании используются стандартные пакеты программ статистического и корреляционного анализа, например Statgraphics, SPSS и др.
2.3. Варианты заданий.
Задание выбирается по последней цифре зачетной книжки (табл. 2.5.).
Исходные данные Спрос на продукцию лесопромышленного предприятия за предыдущего 12 месяцев составляет:
| Месяц | ||||||||||||
| Спрос в условных единицах |
Выполнить:
Установить план производства на первые три месяца следующего периода с вероятностью 0,98 и 0,95.
Прогнозирование выполнить методами наименьших квадратов, экспоненциального сглаживания, скользящей средней, Чебышева. Оценить погрешность. Представить графики и дать выводы.
Таблица 2.5.
Исходные данные для выполнения прогнозирования развития материального потока лесопромышленного предприятия.
| Месяц | ||||||||||||
| вариант | ||||||||||||
Дата добавления: 2021-07-22; просмотров: 514;











