Первое начало термодинамики

Первое начало термодинамики выражает закон сохранения и превращения энергии применительно к процессам в термодинамических системах. Чтобы его сформулировать, введем несколько новых понятий.

В теоретических методах термодинамики используются идеализированные квазистатические или квазиравновесные процессы. Эти процессы идут достаточно медленно, так что на каждом этапе состояние системы можно считать бесконечно близким к равновесному. Значение этой идеализации состоит в том, что для описания мгновенного состояния системы, совершающей квазистатический процесс, требуется столько же параметров, сколько и для описания состояния равновесия.

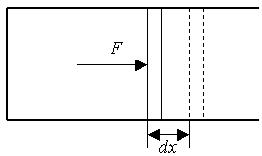Рис. 3.1

Рассмотрим газ в цилиндре с поршнем (рис. 3.1). Площадь поршня S. Когда поршень находится в равновесии, сила F = P×S, с которой газ давит на поршень, должна быть равна по величине и противоположна по направлению внешней силе F¢, с которой действуют на поршень какие-то внешние тела. При квазистатическом расширении или сжатии газа силы F и F¢ продолжают друг друга уравновешивать.

Пусть поршень перемещается на настолько малое расстояние dx, что возможным изменением давления газа можно пренебречь. Тогда работа газа, совершенная в таком бесконечно малом процессе может быть записана в виде

dA = F×dx = P×S×dx = P×dV.

Очевидно, что работа dA¢ внешней силы F¢ в квазистатическом процессе будет по абсолютной величине равна работе газа dA, а по знаку противоположна

dA¢ = - dA = - P×dV.

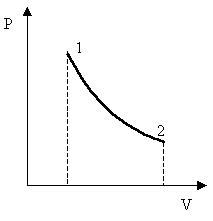Рис. 3.2

Чтобы вычислить работу конечного процесса, в котором объем и давление могут значительно измениться, надо просуммировать элементарные работы dА на бесконечно малых участках процесса, т.е. взять интеграл

.

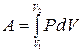Интегрирование проводится от начального объема V₁ до конечного V₂. На графике в P-V координатах работа - это площадь под кривой, изображающей зависимость давления от объема (рис. 3.2).

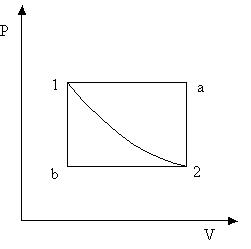Рис. 3.3

Для нахождения интеграла необходимо знать давление как функцию объема. Но, согласно уравнению состояния, Р зависит не только от V, но и от Т. Меняя в ходе процесса различным образом температуру системы, можно квазистатически перевести систему из начального состояния в конечное бесчисленным множеством способов. Каждому из этих способов будет соответствовать своя функция P = P(V), и свое значение интеграла. На рис. 3.3 изображены три пути перехода из состояния 1 в состояние 2. Видно, что работы на этих путях различны.

Работа А не определяется однозначно заданием начального и конечного состояний системы. Ее величина зависит также от способа или «пути» перехода системы из начального состояния в конечное. Про величины такого рода говорят, что они не являются функциями состояния. Напротив, величины, имеющие вполне определенные значения в каждом равновесном состоянии системы, называются функциями состояния. К ним относятся давление, объем, температура и многие другие, с которыми мы встретимся в дальнейшем.

Если процесс происходит при вполне определенных условиях, то работа системы, или работа внешних сил может оказаться равной изменению какой-либо функции состояния. Рассмотрим систему, находящуюся в адиабатической оболочке (адиабатически изолированную). Напомним, что оболочка называется адиабатической, если состояние заключенной в ней системы остается неизменным при любых изменениях температуры окружающих тел, если только значения внешних параметров остаются постоянными. Как показывает опыт, работа внешних сил над адиабатически изолированной системой зависит только от ее начального и конечного состояний, и не зависит от того, каким способом осуществляется переход. При этом производство работы не обязательно должно сопровождаться изменением объема, а может быть связано, например, с преодолением сил трения между частями системы. Опираясь на результаты этих опытов можно постулировать существование внутренней энергии.

Внутренняя энергия U – это функция состояния термодинамической системы, изменение которой во всяком процессе, совершаемом системой в адиабатической оболочке, равно работе внешних сил над системой.

С молекулярно-кинетической точки зрения, внутренняя энергия равна сумме кинетических энергий хаотического теплового движения составляющих систему микрочастиц и потенциальной энергии взаимодействия этих частиц друг с другом. Во внутреннюю энергию не входят кинетическая энергия системы как целого, и ее потенциальная энергия во внешних силовых полях.

Внутренняя энергия является аддитивной функцией состояния, т.е. величина внутренней энергии всей системы равна сумме значений внутренней энергии ее частей.

Если система помещена в адиабатическую оболочку, то единственным способом изменить ее внутреннюю энергию является совершение над ней макроскопической работы внешних сил, что достигается путем изменения внешних параметров. (К числу внешних параметров относятся и силовые поля, в которые помещена система.) Однако если адиабатической изоляции нет, то изменение внутренней энергии возможно и без производства макроскопической работы. Так, при соприкосновении горячего и холодного тел внутренняя энергия переходит от горячего тела к холодному, хотя при этом макроскопическая работа и не совершается.

Процесс обмена внутренними энергиями контактирующих тел, не сопровождающийся производством макроскопической работы, называется теплообменом. Энергия, переданная телу в результате теплообмена, называется количеством теплоты Q, или просто теплотой, полученной системой в таком процессе.

Отметим, что при теплообмене энергия системы может как возрастать, так и убывать, поэтому полученное системой количество тепла Q может быть как положительным, так и отрицательным. В ряде случаев бывает удобнее говорить о количестве тепла Q¢, отданного системой. Очевидно, что при этом Q¢ = - Q.

Таким образом, первое начало термодинамики постулирует существование функции состояния, называемой внутренней энергией, и двух способов ее изменения, связанных с макроскопической работой и передачей тепла. Наиболее распространена следующая формулировка первого начала термодинамики:

Количество тепла Q₁₂, полученное системой при переходе из состояния 1 в состояние 2, равно изменению внутренней энергии DU₁₂ = U₂ – U₁ и работе А₁₂, совершаемой системой в этом процессе

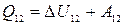. (3.1)

Уравнение (3.1), представляющее математическую формулировку первого начала, чаще записывают для бесконечно малых квазистатических процессов

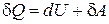. (3.2)

Если система состоит из однородного изотропного вещества, и внешние силовые поля (электрическое или магнитное) отсутствуют, работа связана только с изменением объема (dA = P×dV). Именно такие системы мы чаще всего будем рассматривать. В этом случае первое начало термодинамики принимает вид

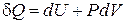. (3.3)

Так же как и совершаемая системой работа, количество теплоты зависит не только от начального и конечного состояний системы, но и от пути перехода, а значит, не является функцией состояния.

В связи с тем, что теплота и работа не являются функциями состояния, для бесконечно малых количеств теплоты и работы принято употреблять обозначения dQ и dA, а не dQ и dA. Этим хотят подчеркнуть, что dQ и dA не могут рассматриваться как полные дифференциалы. Они являются бесконечно малыми величинами, но не приращениями определенных функций.

Теплоемкость

Теплоемкостью системы C называется отношение бесконечно малого количества теплоты dQ, полученного системой, к соответствующему приращению dT ее температуры:

.

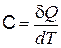Если теплоемкость системы, состоящей из однородного вещества разделить на его массу m, получится удельная теплоемкость. Ее обычно обозначают малой буквой с (с = С/m). В термодинамике более удобно использовать теплоемкость одного моля вещества - молярную теплоемкость С:

.

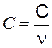Количество тепла, получаемое молем однородного вещества в каком-либо бесконечно малом процессе, можно представить в виде:

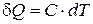. (4.1)

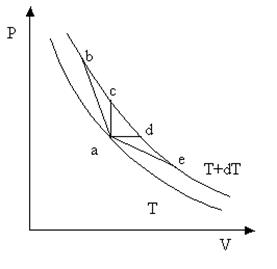Рис. 4.1

Как видно из рис. 4.1, на котором изображены две изотермы с температурами Т и Т + dT, приращение температуры dT еще не определяет полностью того состояния, в которое переходит система в результате процесса. Приращение объемов в процессах a-b, a-c, a-d, a-e различается как по величине, так и по знаку. В этих процессах будут совершены разные работы, и получены разные количества тепла. Поэтому теплоемкость в первую очередь зависит от происходящего в системе процесса. Свойствами вещества определяется теплоемкость только вполне определенного процесса, а не теплоемкость «вообще».

Запишем первое начало термодинамики (3.3) для одного моля однородного и изотропного вещества, выразив dQ через теплоемкость

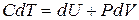. (4.2)

Рассматривая внутреннюю энергию как функцию температуры и объема U = U(T,V), возьмем ее полный дифференциал и подставим в (4.2)

.

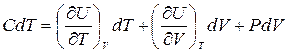Разделив на dT, получим

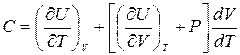. (4.3)

Объем зависит не только от температуры Т, но и от давления Р. В зависимости от происходящего с системой процесса, отношение dV/dT может принять любое значение. Поэтому и теплоемкость С, вообще говоря, может принимать любые значения от -¥ до +¥. В частности, для изотермического процесса С = ±¥, т.к. в этом случае dT = 0, dQ ¹ 0. При адиабатическом процессе dQ = 0, dT ¹ 0, С=0. Чтобы придать выражению (4.3) однозначный смысл, надо задать процесс.

Особенно важны теплоемкости при постоянном объеме и постоянном давлении, обозначаемые C_V и С_Р. Если объем остается постоянным, то dV=0 и, следовательно,

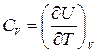. (4.4)

Если постоянно давление, то отношение dV/dT переходит в частную производную (¶V/¶T)_P. В этом случае

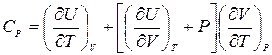. (4.5)

Разность теплоемкостей С_Р – C_V равна

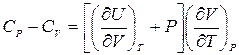. (4.6)

Если ввести новую функцию состояния Н, называемую энтальпией

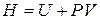, (4.7)

то ее дифференциал dH = dU + PdV + VdP в изобарическом (dP=0) процессе, как видно из соотношения (3.3), будет равен dQ. Тогда

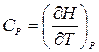. (4.7)

Как мы увидим в дальнейшем, теплоемкости C_V и C_P входят во многие термодинамические соотношения.