Параметры состояния. Уравнение состояния

Равновесные состояния термодинамических систем описываются с помощью небольшого числа различных макроскопических параметров состояния. К ним относятся давление, объем, температура, плотность, концентрация, напряженность электрического или магнитного полей и т.д.

Параметр, значение которого в состоянии равновесия одно и то же для любой части системы и равно его значению для системы в целом, называется интенсивным параметром. Такими параметрами являются температура, давление, плотность.

Объем, масса, количество вещества, число частиц относятся к экстенсивным параметрам. Значения экстенсивных параметров для всей системы равны сумме их значений для ее частей, поэтому они еще называются аддитивными параметрами.

Макроскопические параметры, определяющие состояние системы и ее отношение к окружающим телам, разделяются на внутренние и внешние. Внешние параметры определяются положением и состоянием внешних тел, воздействующих на систему, но в систему не входящих. Внутренние параметры зависят от состояния самой системы. Приведем примеры внутренних и внешних параметров.

Пусть газ находится в сосуде с жесткими стенками. Объем газа определяется положением внешних тел – стенок. В данном случае объем – внешний параметр. Давление, производимое газом на стенку сосуда, зависит от концентрации молекул и средней скорости их теплового движения. Оно является внутренним параметром.

Рассмотрим теперь газ, заключенный в вертикальном цилиндре под поршнем, который может свободно перемещаться. Пусть на поршне лежит гиря. В этом случае давление газа будет являться внешним параметром, так как оно будет определяться весом груза и поршня, а также атмосферным давлением. Объем же теперь становится внутренним параметром, так как положение поршня с грузом зависит от внутреннего давления, производимого газом на поршень.

В состоянии термодинамического равновесия каждый внутренний параметр является функцией внешних параметров и температуры системы. Это утверждение, являющееся обобщением опытных фактов, постулирует существование уравнений состояния. Примером может являться уравнение состояния идеального газа PV=nRT (1.1). Из этого уравнения следует, что для заданного количества газа мы можем произвольно задавать только два параметра, например T и V. Давление при этом будет однозначно определено, и его можно считать функцией температуры и объема P = P(T,V). Минимальное число параметров состояния, которые необходимо задать, чтобы полностью определить состояние системы называют числом термодинамических степеней свободы. Опыт показывает, что давление, объем и температура находятся в функциональной зависимости не только для идеальных, но и для реальных газов, а также для любых однородных и изотропных тел. Если количество вещества в таких системах фиксировано, то число термодинамических степеней свободы равно двум. Существование функциональной связи можно выразить соотношением, представляющим наиболее общую запись уравнения состояния

f(P,V,T) = 0. (2.1)

Вид функции f(P,V,T) различен для различных систем. Уравнение состояния является важнейшей характеристикой термодинамической системы. Его нельзя вывести теоретически из общих принципов термодинамики. Уравнения состояния получают либо из опыта, либо методами статистической физики.

Благодаря наличию уравнения состояния, изменения параметров системы не независимы, а связаны определенным образом. Ряд важных соотношений может быть установлен без знания конкретного вида функции f(P,V,T). Для получения одного из таких соотношений разрешим уравнение (2.1) относительно одной из переменных, например Р, т.е. представим давление в виде функции двух переменных Т и V: P = P(T,V). Если поддерживать объем постоянным, а температуру изменить на бесконечно малую величину dT, то давление получит также бесконечно малое приращение, пропорциональное dT

.

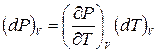Нижний значок V здесь означает, что приращения температуры и давления берутся при постоянстве объема. Коэффициент пропорциональности (¶Р/¶Т)_V, связывающий (dP)_V и (dT)_V, является частной производной давления по температуре при постоянном объеме. Частными производными в математике называются производные, получаемые дифференцированием какой-либо функции двух или нескольких аргументов по одному из них в предположении, что все остальные аргументы остаются постоянными.

Пусть теперь температура Т остается постоянной, а объем V получает бесконечно малое приращение dV. Тогда соответствующее приращение давления представится выражением

.

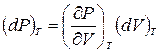Если, наконец, изменяются и температура Т и объем V, то с точностью до бесконечно малых высшего порядка приращение давления представится суммой dP = (dP)_V + (dP)_T, или

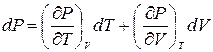. (2.2)

Это выражение является полным дифференциалом давления P(T,V), рассматриваемого как функция температуры и объема.

Рассмотрим теперь процесс, в котором давление остается постоянным (P = Const, dP = 0). Тогда приращения (dT)_Р и (dV)_Р, которые берутся при постоянном давлении, не будут независимыми. Они окажутся связанными соотношением, вытекающим из (2.2)

.

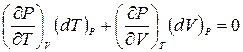Если разрешить это уравнение относительно (dV)_P/(dT)_P, то полученная таким образом величина даст частную производную (¶V/¶T)_P. Таким образом,

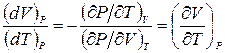. (2.3)

Пользуясь тем, что

,

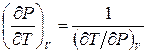выражение (2.3) можно переписать в виде

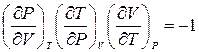. (2.4)

Следует отметить, что для справедливости этого соотношения совершенно не существенно, какой физический смысл имеют величины P, V, T. Оно является чисто математическим тождеством, выражающим в дифференциальной форме наличие функциональной связи между величинами P, V, T.

Тождества вида (2.4) широко используются в термодинамике.