Связь модулей объемной упругости с теплоемкостями

Модуль объемной упругости К, также называемый модулем всестороннего сжатия, показывает, насколько сильно меняется давление при изменении объема. Он является коэффициентом пропорциональности, связывающим изменение давления и относительное изменение объема

.

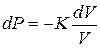Так как давление зависит не только от объема, но и от температуры, K определяется не только веществом, но и условиями сжатия. Наиболее важными являются адиабатический K_ад и изотермический К_Т модули объемной упругости. Они определяются соотношениями

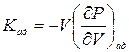и .

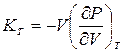В предыдущем параграфе было показано, что для идеального газа

.

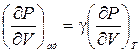Отсюда следует, что K_ад = g K_Т. Покажем, что такое соотношение между адиабатическим и изотермическим модулями объемной упругости имеет место не только для идеального газа, но и для любого однородного и изотропного вещества. При выводе будем пользоваться фактом существования уравнения состояния (не зная его конкретного вида) и первым началом термодинамики

f(P,V,T) = 0,

dQ = dU + PdV.

Запишем первое начало термодинамики для адиабатического (dQ = 0) процесса

dU + PdV = 0.

Рассматривая внутреннюю энергию как функцию температуры и объема U=U(T,V), возьмем ее полный дифференциал

dU = (¶U/¶T)_V dT + (¶U/¶V)_T dV

и подставим в предыдущее выражение. Учитывая, что (¶U/¶T)_V = C_V получим

C_V dT + [(¶U/¶V)_T + P]dV = 0.

Из соотношения (4.6) следует, что выражение в квадратных скобках равно (Cp – C_V)(¶T/¶V)_P.

Тогда

C_V dT + (C_P – C_V)(¶T/¶V)_P dV = 0. (7.1)

Напомним, что рассматривается адиабатический процесс, и приращения dV и dT связывают температуру и объем на адиабате. Обозначая, как обычно, С_Р/С_V = g, можно эту связь представить в виде

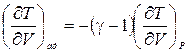. (7.2)

Соотношение (7.2) в каких-то ситуациях может оказаться весьма полезным, но сейчас нас интересует связь давления с объемом.

Рассматривая температуру как функцию давления и объема T = T(P,V), возьмем ее полный дифференциал dT = (¶T/¶P)_V dP + (¶T/¶V)_P dV и подставим в уравнение (7.1). После упрощений получим

,

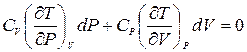или .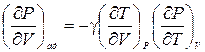

Воспользовавшись тождеством (2.4) легко убедиться, что (¶T/¶V)_P(¶P/¶T)_V = - (¶P/¶V)_T.

Окончательно получим .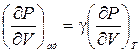

Значит K_ад = g K_Т для любого однородного и изотропного вещества.