ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.

Площадь плоской фигуры

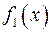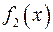Уже отмечалось выражение площади криволинейной трапеции через определенный интеграл. Отсюда следует формула для вычисления площади фигуры, ограниченной сверху и снизу графиками функций и , а с боков прямым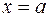и и :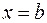

.

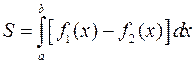В случае если криволинейная трапеция ограничена сверху линией, заданной параметрическими уравнениями: 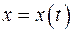, , 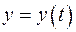, 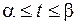площадь фигуры вычисляют следующим образом

,

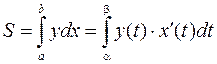где расстановка пределов осуществляется в соответствии со значениями: , .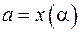

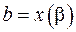Пример. Вычислить площадь фигуры, ограниченной эллипсом: .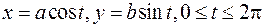

Рассмотрим половину фигуры, лежащую в верхней полуплоскости. Слева направо предельными значениями координаты 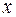служат числа 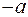и 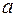. в соответствии с ними определяем пределы интегрирования по параметру 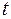из соотношени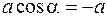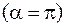й: и 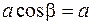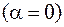. По формуле находим

;

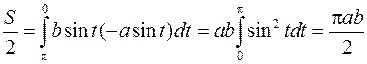откуда для площади, лежащей внутри эллипса получаем формулу .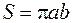

В качестве упражнения рекомендуется вывести формулу для вычисления площади фигуры, заданной в полярный координатах, границами которой служат лучи 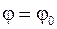, 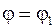и кривая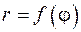

.

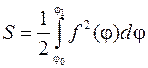Длина дуги кривой

Пусть дуга 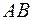кривой представляет собой график функции 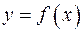, непрерывной на отрезке 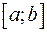. Длину дуги такой кривой определим как предел, к которому стремится длина вписанной ломаной линии (см. рис. 2) пр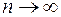и и .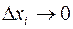

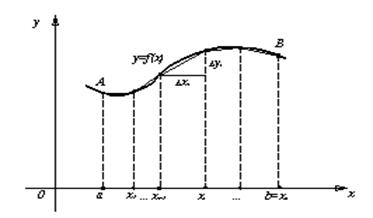
Рис. 2

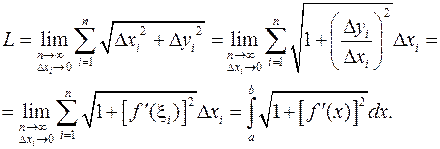
Такое определение длины дуги кривой соответствует интуитивным представлениям и лежит в основе логически строгого понятия длины.

При задании кривой параметрическими уравнениями: 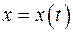, , 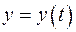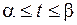из равенства (12) получается формула

.

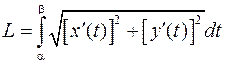Задание дуги кривой уравнением в полярных координатах: 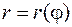, 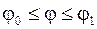является частным случаем параметрического задания: 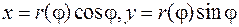. После подстановки данных функций получим формулу для длины дуги кривой, заданной в полярных координатах

.

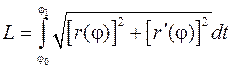Пример. Вычислить длину дуги первой арки циклоиды (траектории точки обода колеса), показанной на рис. 3.

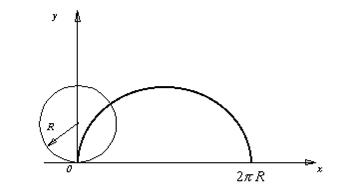
Рис. 3

Циклоида имеет параметрические уравнения: 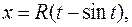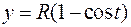. Параметром 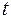служит угол поворота колеса, который для первой арки принимает значения 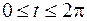. Согласно (13) длина дуги циклоиды выражается интегралом

.

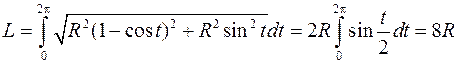Объем и площадь поверхности тела вращения

Поставим задачу определения объема и площади поверхности тела, полученного вращением дуги кривой 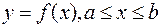вокруг оси .

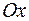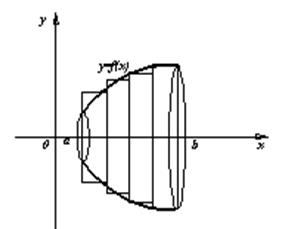
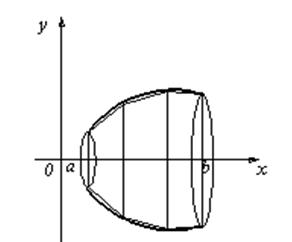
Рис. 4 Рис. 5

Объем определяем как предельное значение объема составного цилиндрического тела, показанного на рис. 4. Поверхность тела вращения получается в пределе площади составной поверхности из вписанных конических поверхностей (см. рис. 5).

В итоге приходим к формулам для вычисления объема 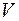и площадь поверхности :

;

.

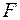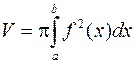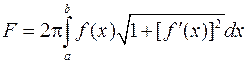Обратите внимание, что использование составного цилиндрического тела не дает правильного значения площади поверхности.