Метод половинного деления.

Метод половинного деления является одним из простейших методов решения нелинейных уравнений, и один из самых распространённых.

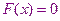
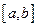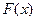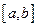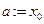
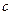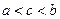Допустим, нам удалось найти отрезок, на концах которого функция имеет разный знак. В этом случае можно быть уверенным, что на отрезке содержится, по крайней мере, один корень уравнения и (если 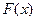- непрерывная)

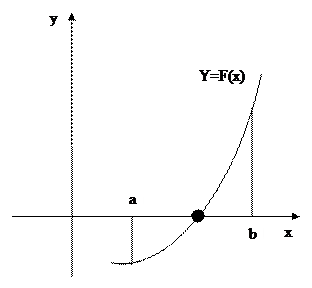
Число корней n+1, n – четное.

В качестве начального приближения берем точку, 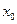находящуюся на середине отрезка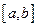

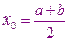
и получаем два отрезка 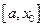и 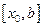затем проверяем на концах, какого из этих двух отрезков функция 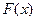имеет разный знак. Если знак у 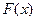разный на отрезке 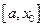, то полагаем 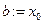и получаем новый отрезок 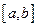, содержащий 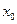. Если на отрезке 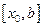, то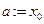

Полученный сокращенный отрезок 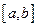делим пополам и получаем .

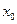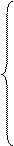If 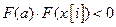, then

else ,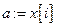

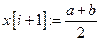
При этом надо учитывать, что итерационный процесс может быть расходящимся. Но метод половинного деления обладает значительным преимуществом – он всегда сходится. На итерационном шаге с номером 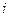будет достигнута точность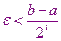

Недостатком этого метода является достаточно медленная сходимость.

Метод 11