Погрешности численных методов.
При использовании любого численного метода возникают погрешности, которые могут быть очень велики.
С помощью математической модели научная или интегральная задача сводится к математической, а для решения математической задачи в большинстве случаев приходится использовать численные методы, которые математическую задачу сводят к выполнению конечного, но весьма большого числа простейших арифметических действий(+,-,*,/).
Численные методы требуют большого объёма вычислений, поэтому вручную эти методы применяются очень редко. Поэтому численное решение производится с помощью средств вычислительной техники.
При численном решении всегда возникают погрешности. Возможны грубые ошибки, промахи они могут быть связаны:
1) с неправильной постановкой задачи;
2) с неверно построенной моделью;
3) с ошибками в составлении программы;
4) с аппаратными сбоями ПК, но последние бывают крайне редко.
Грубые ошибки могут быть устранены при отладке программы. Даже если грубые ошибки устранены, сохраняются следующие типы погрешностей:
1) ошибки математической модели;
2) ошибки в исходных данных;
3) ошибки численного метода;
4) ошибки округления.
Теперь рассмотрим виды погрешностей более подробно.
1) Погрешности обусловленные ошибкой математической модели связаны с неадекватностью используемой модели оригиналу.
2) Ошибки в исходных данных также приводят к погрешности в результатах.
Первые два типа ошибок относятся к неустранимым погрешностям, так как они не могут быть уменьшены в процессе решения математической задачи.
Неустранимые ошибки можно уменьшить только за счет уточнения математической модели и более точного задания его параметров.
3) Большинство численных методов сводит математическую операцию к конечному числу арифметических действий – это ведет к появлению ошибки численных методов.
Например, вычисление интеграла сводится к вычислению интегральной суммы.
Как правило, ошибки численного метода регулируемые. К примеру, при численном вычислении интеграла точность можно повысить, увеличив число слагаемых интегральной суммы. А в общем случае путем изменения некоторого параметра. Значение погрешности численного метода и пути её уменьшения рассматривается при анализе конкретных численных методов.
4) Ошибки округления связаны с ограниченным числом разрядов в числах, с которыми оперирует ЭВМ. Хотя удельная точность выполнения каждой операции в большинстве случаев достаточно высока, малые погрешности имеют тенденцию к накоплению и если общее число операций достаточно высоко, итоговая погрешность может быть недопустимо большой.
Самый простой путь снижения ошибок этого типа состоит в повышении точности представления чисел на ЭВМ. Например, в замене типа Real на Double или Extended. Однако, такой путь повышения точности не самый лучший.
Кроме того, использование чисел большой разрядности приводит к нерациональному использованию ресурсов ЭВМ.
Например, вычислим 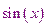 , разложив его с помощью ряда Тейлора.
, разложив его с помощью ряда Тейлора.
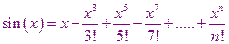
Погрешность будет равна величине последнего отбрасываемого слагаемого.
Если мы точность обозначим за 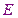 , то компьютер будет считать пока
, то компьютер будет считать пока 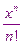 <
< 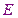 .
.
И получим 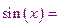 20,….. Но этот результат абсолютно неверен! Так в чем же состоит наша ошибка? Почему Верный с логической точки зрения ход вычисления дал неправильный результат?
20,….. Но этот результат абсолютно неверен! Так в чем же состоит наша ошибка? Почему Верный с логической точки зрения ход вычисления дал неправильный результат?
Для нахождения ответа на этот вопрос рассмотрим возникновение ошибок связанных с округлением.
Рассмотрим возникновение ошибок округления на нескольких конкретных примерах. Предположим, что ЭВМ оперирует с 4-мя разрядами цифр, то есть результат представляется 4-мя значащими цифрами, это значит, что относительная ошибка составляет 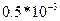
Ошибки округления возникают при всех арифметических операциях. Например, при суммировании:
+ 9870
11104 округляем и получаем
11100
4 – погрешность.
Относительная ошибка значительно возрастает при вычитании двух близких по величине чисел:
0,00005 – абсолютная погрешность.
0,00005 – относительная погрешность.
0,1234
- 0,1233
0,0001 + 0,0001
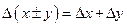 -погрешность суммы
-погрешность суммы
Таким образом, в результате вычисления двух близких по величине цифр погрешность = 100%. Поэтому при программировании нужно создавать программу таким образом, чтобы избежать вычитания двух близких по величине цифр.
Для ошибок округления не выполняются обычные правила арифметики.
Например, ошибка суммы нескольких чисел зависит от порядка суммирования.
Предположим нам нужно сложить 4 числа:
1234 0,2 0,3 0,4
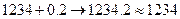
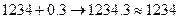
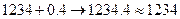
Таким образом, 1234+0,2+0,3+0,4=1234 ,но на самом деле эта сумма =1234,9 , то есть погрешность =0,9.
Но если мы изменим порядок суммирования

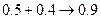
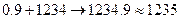 то ,
то ,
0,2+0,3+0,4+1234=1235 и тогда погрешность вычисления будет = 0,1.
Погрешность зависит от последовательности, в которой производится вычисление. Ошибка будет меньше, когда вычисление начинается с меньших по абсолютной величине цифр.
Для уменьшения ошибок округления необходимо придерживаться следующих правил:
1) По возможности избегать вычитания двух близких по величине чисел;
2) Сложение и вычитание длинной последовательности чисел начинать с наименьших чисел;
3) Использовать выражения 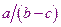 или
или 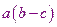 вместо
вместо 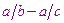 и
и 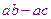 ;
;
4) В любых случаях сводить к минимуму число арифметических операций.
Еще один тип ошибок связан с ограничением представления чисел на ЭВМ. Все числа в ПК по абсолютной величине находятся в интервале 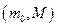 где
где 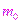 - машинный ноль, а
- машинный ноль, а 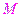 - машинная бесконечность.
- машинная бесконечность.
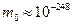
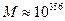
И если 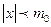 , то компьютер посчитает что
, то компьютер посчитает что 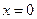 , а если
, а если 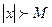 , то компьютер примет
, то компьютер примет 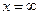 , произойдет переполнение памяти и компьютер перестанет работать. Пусть
, произойдет переполнение памяти и компьютер перестанет работать. Пусть

Нужно помнить о машинном нуле, потому что он намного более опасен из-за трудности обнаружения.
Дата добавления: 2017-03-12; просмотров: 5073;











