Решение нелинейных уравнений.

Задача нахождения корней нелинейного уравнения возникает достаточно часто.

Нелинейные уравнения делятся на алгебраические и трансцендентные. Для алгебраического уравнения 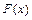- это полином некоторой степени больше единицы.

Хотя алгебраические и трансцендентные уравнения часто решают одними и теми же методами, но существуют численные методы, использующие свойства алгебраических уравнений. Методы решения делятся на прямые и итерационные. Прямые методы позволяют найти решения уравнений непосредственно с помощью формул.

Пример: Решение квадратного уравнения по формулам Виета. В итерационных методах задаётся процедура решения в виде многократного применения некоторой процедуры. В этом случае нахождение корня уравнения состоит из двух этапов.

1 этап: отыскание приближенного значения корня или содержащего его отрезка.

2 этап: уточнение приближенного значения корня до некоторой заданной точности. Приближенное значение корня (начальное приближение) может быть найдено различными способами:

1) из физических соображений

2) из решения аналогичной задачи при других исходных данных;

3) графическим методом.

Если удалось найти две точки, образующих отрезок, 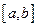на концах которого 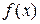имеет различный знак, то в качестве начального приближения можно взять середину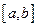

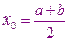
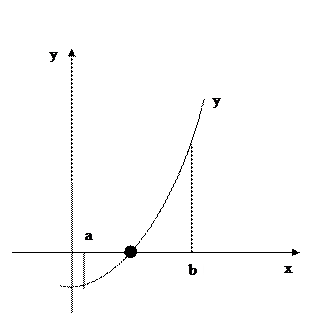
Если знак разный, то это гарантирует, что между ними будет хоть один корень.

Итерационный процесс состоит в последовательном уточнении начального приближения. Каждый такой шаг называется итерацией. В результате получается последовательность приближенных значений корня. Если эта последовательность с ростом 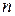(числа итераций) приближается к истинному значению корня, то итерационный процесс сходится. К сожалению, часто бывает, что итерационный процесс не сходится. Поэтому надо следить за условиями сходимости и предусмотреть возможность расхождения итерационного процесса.

Метод 10