Свойства численного решения.
Ошибки в исходных данных приводят к ошибке результата, можно ожидать, что небольшие ошибки в исходных данных приводят к возникновению небольшой ошибке результата.
Пусть 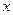 - исходная величина
- исходная величина
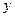 - результат вычисления
- результат вычисления
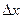 - ошибка исходных данных
- ошибка исходных данных
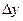 - Ошибка результата
- Ошибка результата
Если результат вычисления 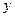 непрерывно зависит от исходной величины
непрерывно зависит от исходной величины 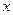 , то есть небольшие погрешности в исходных данных приводят к небольшим погрешностям результата, то задача называется устойчивой.
, то есть небольшие погрешности в исходных данных приводят к небольшим погрешностям результата, то задача называется устойчивой.
Если при любых значениях параметров решение задачи существует, единственно и устойчиво, то задача называется корректной. В дальнейшем мы будем рассматривать только корректные задачи.
Существует ряд прикладных некорректных задач, для решения которых разработаны специальные методы – методы решения некорректных задач.
Важнейшим свойством численного метода является его сходимость. Она означает, приближение численного решения к истинному, при изменении некоторого параметра численного метода (например, приближение результата численного вычисления результата интеграла к истинному значению при увеличении числа слагаемых в интегральной сумме).
В численных методах широко используется итерационный метод. Это метод последовательного приближения, когда сначала находится первое приближение решения задачи 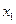 , потом с помощью
, потом с помощью 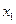 находится второе приближение
находится второе приближение 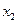 и так далее.
и так далее.
Если последовательность 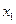 ,
, 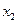 ,…
,… 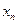 стремится к точному решению, то говорят о сходимости итерационного процесса.
стремится к точному решению, то говорят о сходимости итерационного процесса.
Тема №2
Дата добавления: 2017-03-12; просмотров: 2105;











