Уравнение состояния идеальных газов

<1 2 345 6 7 >

Законы Бойля—Мариотта, Гей-Люссака и Шарля устанавливают связь только между двумя из трех основных параметров газа р, v и Т при условии, что значение третьего параметра остается постоянным. Уравнение состояния идеального газа устанавливает связь между всеми тремя основными его параметрами.

Допустим, что идеальный газ, заключенный в цилиндре с поршнем имеет параметры p₁, v₁ и T₁, (рис. 2, а). Если уменьшить давление газа в цилиндре и подвести к нему некоторое количество теплоты, то газ перейдет в новое состояние, где будут иметь место параметры р₂, v₂ и Т₂ (рис. 2, б).

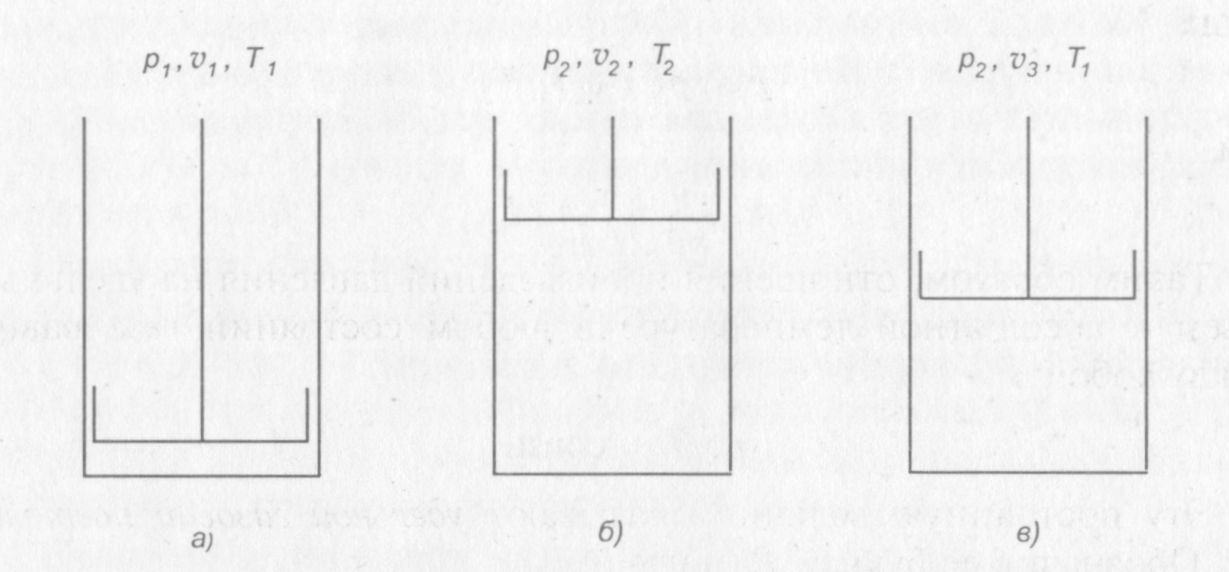
Рис. 2. Иллюстрация уравнения состояния идеального газа

Чтобы установить связь между начальным и конечным состояниями газа, осуществим переход из первого состояния в последнее двумя промежуточными операциями. Сначала уменьшим давление газа от р₁ до р₂, поддерживая температуру T₁ постоянной путем подвода теплоты к газу. Тогда газ окажется в промежуточном состоянии (рис. 2, в) и будет иметь параметры р₂, v₃ и T₁. Затем будем подогревать газ так, чтобы он продолжал расширяться, сохраняя свое давление неизменным, его температура при этом повысится до Т₂(рис. 2, б).

Сопоставим эти три состояния газа. Так как в первом состоянии и третьем температуры одинаковы, то между удельными объемами и давлением газа в этих состояниях должна по закону Бойля—Мариотта существовать следующая связь:

,

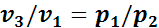тогда

.

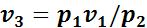Так как в третьем и втором состояниях давления одинаковы, то по закону Гей-Люссака

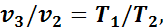
откуда

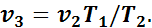
Тогда

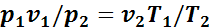
или

.

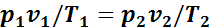Таким образом, отношения произведений давления на удельный объем к абсолютной температуре в любом состоянии газа равны между собой:

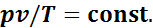
Эту постоянную величину называют удельной газовой постоянной. Обозначив ее буквой R, получим

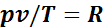
или

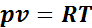. (1.1)

Уравнение (1.1) называется уравнением идеального газа, или уравнением Клайперона.

Для использования уравнения Клайперона необходимо определить численное значение газовой постоянной для данного газа по справочным материалам. Газовая постоянная становится универсальной, т. е. одинаковой для всех газов, если количество газа выразить в киломолях. Умножив левую и правую часть уравнения (1.1) на мыссу 1 кмоля, получим:

,

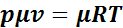где μ — молекулярная масса газа.

На основании закона А. Авогадро, который устанавливает, что при одинаковых температурах и одинаковых давлениях равные объемы различных идеальных газов содержат одинаковое число молекул, было установлено значение универсальной газовой постоянной:

.

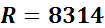Для 1 кмоля газа уравнение состояния можно представить как

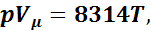(1.2)

где V_μ — объем 1 кмоль газа.

Уравнение (1.2) носит название уравнения Клайперона— Менделеева. Зная значение относительной молекулярной массы μ, можно определить газовую постоянную любого газа:

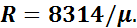
Теплоемкость газов

Теплоемкостью газа, как и любого другого тела, называется количество теплоты, необходимое для нагрева тела на один градус.

Теплоемкость единицы количества вещества называется удельной теплоемкостью. Так как в термодинамике рассматривается главным образом удельная теплоемкость, то ее можно называть просто теплоемкостью.

Если единице количества вещества сообщить (или отвести от нее) какое-то количество теплоты (q) и если при этом происходит изменение температуры данного вещества от Т₁ до Т₂, то отношение теплоты q к разности данных температур представляет собой среднюю теплоемкость (с) газа в пределах от Т₁до Т₂:

следовательно,

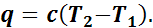(1.3)

Теплоемкость вещества и в частности газа зависит от его природных свойств, а также от условий, в которых происходит процесс изменения его состояния, от температуры, а для реальных газов и от давления.

Теплоту можно подводить к рабочему телу различными способами. В термодинамике широко используется два способа подведения теплоты:

1) при постоянном удельном объеме (изохорный способ);

2) при постоянном давлении рабочего тела (изобарный способ).

Изохорный подвод теплоты происходит в цилиндре с неподвижным поршнем, изобарный — в цилиндре с подвижным поршнем при увеличении объема, давление при этом остается постоянным.

Величина q в соответствии с формулой (1.3) зависит не только от соотношения температур, но и от способа подвода теплоты. Поэтому различают теплоемкость при постоянном объеме с_v (изохорная теплоемкость) и теплоемкость при постоянном давлении с_р (изобарная теплоемкость).

<1 2 345 6 7 >

Дата добавления: 2017-02-13; просмотров: 2015;