Обратимые и необратимые процессы

<3 4 567 8 9 >

Термодинамическим процессом называется последовательное изменение состояния рабочего тела, при котором параметры его состояния (все или некоторые) изменяются, а масса рабочего тела, совершающего процесс, остается неизменной.

В термодинамике широко используется диаграмма, в которой по оси абсцисс откладываются значения удельных объемов v, а по оси ординат — значения давлений р.

По координатам р и v можно определить состояние рабочего тела.

Если тело перешло из состояния 1 в состояние 2 через ряд состояний а, b, с и др., то это означает, что тело совершило термодинамический процесс. Проведя через эти точки кривую, получим линию процесса на р—v диаграмме (рис. 3).

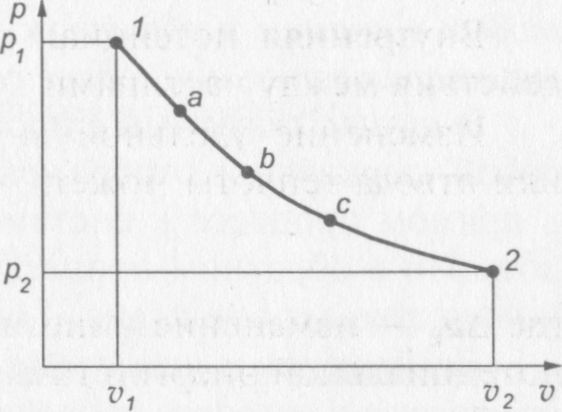
Рис. 3. р—v диаграмма

При изменении своего состояния газ совершает работу против внешних сил (процесс расширения) или воспринимает работу этих внешних сил (процесс сжатия).

Если подводить к газу теплоту, то поршень (рис. 4) в результате расширения газа переместится слева направо, и газ совершит работу при постоянном давлении:

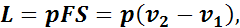
где р — постоянное давление газа;

F — площадь поршня;

S — ход поршня,

v₁, v₂ — начальный и конечный объемы газа.

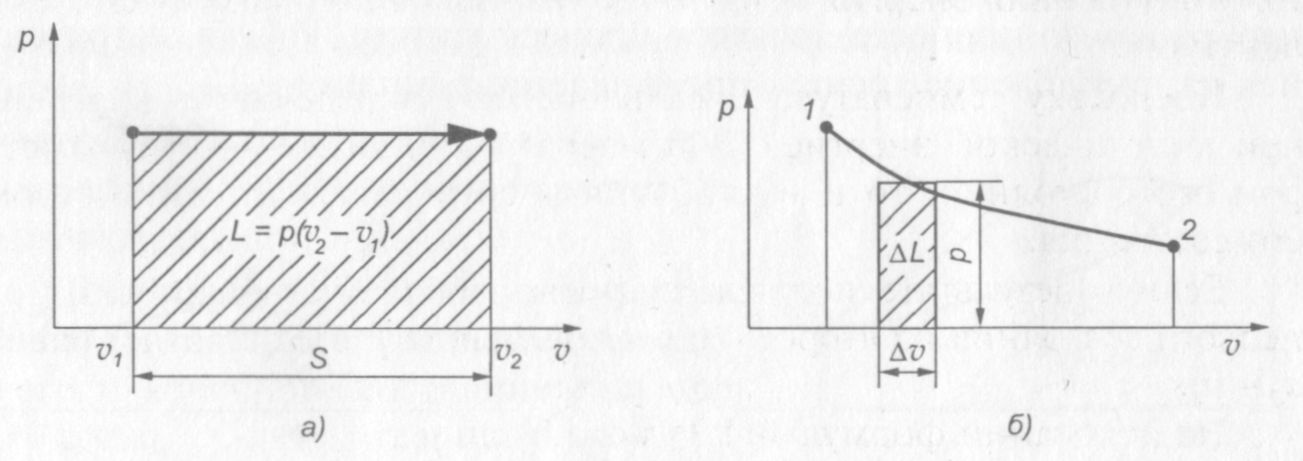
Рис. 4. Работа расширения газа: а — при р = const;
б — при переменном давлении, ∆L = Σp ∆v

В p—v диаграмме эта работа изображается площадью заштрихованного прямоугольника.

Если рассмотреть произвольный процесс, то очевидно элементарную работу расширения ∆L можно подсчитать как площадь элементарного прямоугольника с основанием ∆v и высотой р, а вся работа будет равна сумме площадей таких прямоугольников.

Таким образом, работа расширения газа будет равна площади, ограниченной сверху кривой процесса, снизу — осью абсцисс, а слева и справа двумя крайними ординатами процесса, соответствующими начальному и конечному состояниям газа.

Работа не является только функцией состояния газа, так как она зависит и от характера процесса.

На рис. 5 показаны два различных процесса перехода газа из состояния 1 в состояние 2. Работы этих процессов не равны при одинаковых начальных и конечных состояниях газа: L₁ = s_m_1а2п > L₂ = s_m₁_b₂_n (s — площадь).

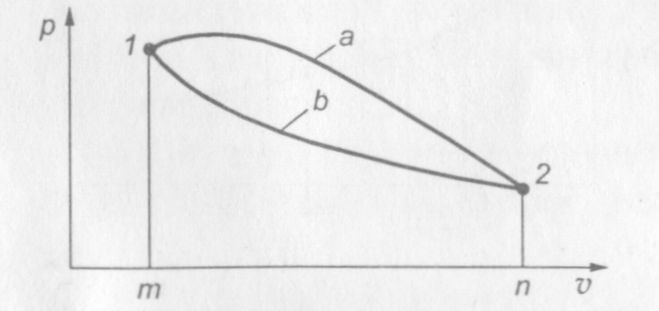
Рис. 5. Два различных процесса расширения газа

Это свойство работы как функции процесса и позволило создать периодически действующие тепловые машины. В тепловом двигателе работа расширения всегда больше работы, затраченной на сжатие. Полученная таким образом разность работ (согласно первому закону термодинамики эквивалентна применяемой в двигателе теплоте) используется для различных целей.

Обратимыми называются процессы, в результате совершения которых в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние.

В случае обратимых процессов обратный процесс представляет собой «зеркальное отображение» прямого процесса: если, например, в прямом процессе к системе подводится какое-то количество теплоты, то в обратном процессе от системы отводится точно такое же количество теплоты (рис. 6).

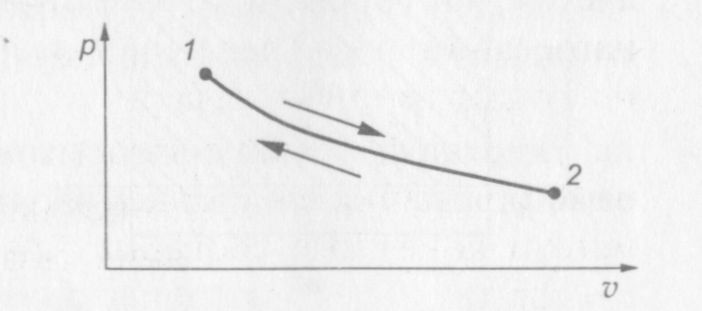
Рис. 1.6. p—v диаграмма обратимого процесса

Необратимым называется процесс, при котором система не возвращается в исходное состояние.

Все естественные самопроизвольные процессы необратимы. Обратимых процессов в природе не существует.Типичным примером необратимого процесса является процесс трения. Работа, затраченная на преодоление трения, превращается в теплоту.

Рабочее тело может произвести работу только при переходе из неравновесного состояния в равновесное. На рис. 7, а представлена схема перехода газа из неравновесного состояния в равновесное. Предварительно сжатый газ находится в цилиндре под застопоренным поршнем в неравновесном состоянии под давлением р₁. Давление окружающей среды р значительно меньше, чем давление газа. При удалении стопора G поршень начнет перемещаться вправо из-за разности давлений.

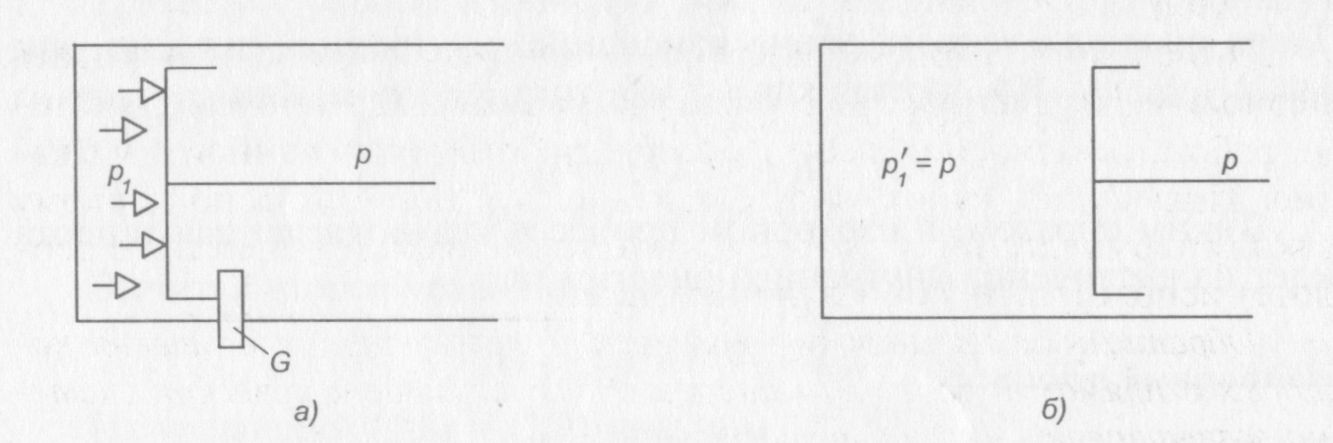
Рис. 7. Схема перехода газа из неравновесного состояния (а) в равновесное (б)

Поршень будет перемещаться только до тех пор, пока давление под поршнем не станет равно давлению окружающей среды (рис. 7, б), т. е. работа будет совершаться до тех пор, пока система не придет в состояние равновесия.

Изохорный процесс

Изохорными называются процессы, протекающие при постоянном объеме. К таким процессам относятся нагревание или охлаждение газа в сосуде постоянного объема: v = const.

На рис. 8 показана p—v диаграмма изохорного процесса.

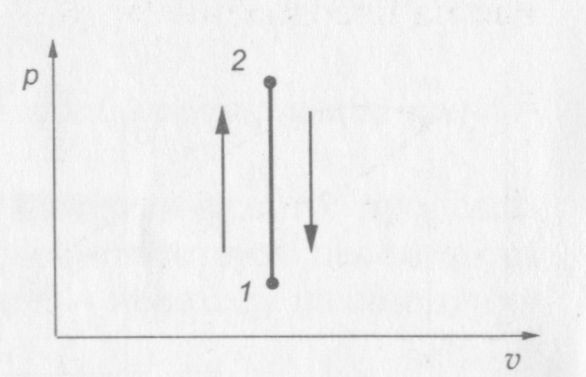
Рис. 8. р—v диаграмма изохорного процесса

Переход газа из состояния 1 в состояние 2 сопровождается нагреванием газа, а переход из состояния 2 в состояние 1 — охлаждением. Направление процесса определяется по изменению давления: при нагревании газа давление растет, а при охлаждении — падает.

Для определения соотношения параметров напишем уравнения начального и конечного состояния газа при v = const:

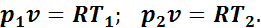
Разделим почленно второе уравнение на первое, получим

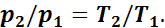(1.5)

Выражение (1.5) показывает, что в изохорном процессе давление газа прямо пропорционально абсолютной температуре.

Изменение удельной внутренней энергии в изохорном процессе (как и во всех процессах) определяется по формуле

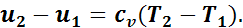(1.6)

В процессе при постоянном объеме внешняя работа не совершается, т. е. удельная работа изменения равна нулю:

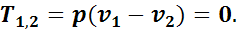
Тогда внешняя теплота равна изменению внутренней энергии, так как q₁,₂ = ∆u + Al₁,₂, но так как l₁,₂ = 0, то q₁,₂ = u₂- u₁, или

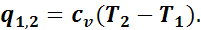
Таким образом, в изохорном процессе вся подведенная теплота идет на увеличение внутренней энергии газа.

Изобарный процесс

Изобарными процессами называются процессы, протекающие при постоянном давлении: р = const.

На рис. 9 показана p—v диаграмма изобарного процесса.

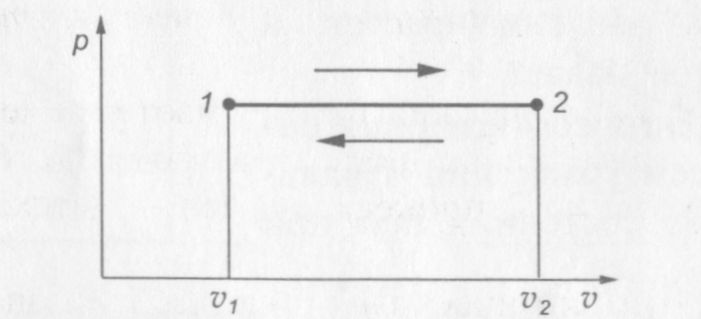
Рис. 9. p—v диаграмма изобарного процесса

Процесс расширения газа на диаграмме соответствует переходу из состояния 1 в состояние 2, а процесс сжатия — переходу из состояния 2 в состояние 1.

Для определения соотношения параметров напишем уравнение начального и конечного состояний газа при р = const:

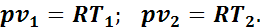
Разделив почленно второе уравнение на первое, получим

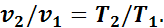(1.7)

Выражение (1.7) показывает, что в изобарном процессе объемы газа пропорциональны абсолютным температурам.

Изменение внутренней энергии, как известно, не зависит от вида процесса и поэтому для изобарного процесса определяется так же, как и для всех процессов:

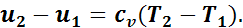
Удельная работа газа в этом случае будет равна площади прямоугольника, основанием которого служит отрезок абсциссы v₂—v₁, а высотой — отрезок ординаты р:

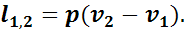(1.8)

Уравнение работы изменения объема идеального газа в изобарном процессе можно представить и в другом виде, написав для этого два уравнения состояния газа (одно для конечного состояния, другое — для начального):

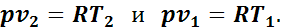
Вычитая второе уравнение из первого, получим

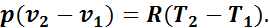(1.9)

Из уравнений (1.8) и (1.9) получим

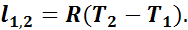(1.10)

Теплота, которая сообщается газу в изобарном процессе, на основании первого закона термодинамики может быть найдена по формуле

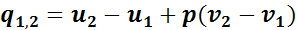
или по общей формуле

<3 4 567 8 9 >

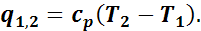
Дата добавления: 2017-02-13; просмотров: 2752;