Динамика твердого тела

1. Вращение твердого тела вокруг неподвижной оси. Момент инерции твердого тела.

Пусть абсолютное твердое тело вращается вокруг закрепленной оси с некоторой угловой скоростью 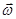(рис. 45). Разобьем все твердое тело на элементарные массы 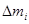, положение которых относительно начала отсчета 0 задается их радиус-векторами 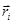. Каждая элементарная масса при этом движется по окружности радиуса R_i с линейной скоростью V_i . Момент импульса этой элементарной массы относительно начала 0 равен:

.

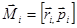Найдем модуль этого момента импульса относительно точки:

.

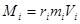Вектор момента импульса элементарной массы направлен перпендикулярно плоскости, в которой расположены векторы 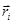и .

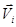Рис.45

Поскольку 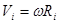, можем сделать следующие преобразования:

.

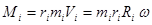Найдем проекцию вектора момента импульса на ось вращения z:

.

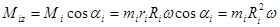Просуммируем по всем частицам тела и получим проекцию на ось z полного момента импульса:

.

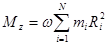Назовем моментом инерции материальной точки относительно оси величину:

.

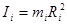Здесь 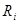- радиус окружности, которую описывает элементарная масса (точка) при вращении всего тела.

Тогда величину, равную сумме моментов инерции всех элементарных масс твердого тела относительно оси, назовем моментом инерции твердого тела относительно оси:

.

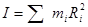Видно, что момент инерции зависит не только от массы, но и от распределения масс тела в пространстве.

Проекция момента импульса всего тела на ось вращения принимает вид:

.

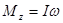2.Расчет моментов инерции твердых тел правильной формы:
дискретное и непрерывное распределение масс. Примеры.

Из определения момента инерции твердого тела:

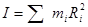
следует, что он является величиной аддитивной. Рассмотрим два случая распределения масс: дискретное и непрерывное.

1. Дискретное распределение масс.
В этом случае следует найти момент инерции каждой массы относительно некоторой оси и суммировать все найденные значения.

2. Непрерывное распределение масс.
В этом случае вводится понятие объемной плотности тела 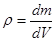. Здесь dm –элементарная масса тела. Тогда можем записать 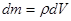. По определению момента инерции твердого тела:

.

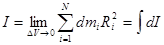Здесь dI =R² dm – момент инерции элементарной массы.

Рассчитывать моменты инерции тел по этой формуле можно в тех случаях, когда расчет момента инерции не вызывает математических трудностей, поскольку здесь, вообще говоря, стоит интеграл по объему. В некоторых случаях этот интеграл можно свести к линейному, например, для тел правильной формы.

Рассмотрим несколько примеров расчетов моментов инерции тел правильной формы.

1. Момент инерции однородного стержня массой m и длиной 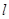относительно оси, проходящей через его центр масс перпендикулярно стержню.
   Необходимые обозначения сделаны на рис. 46

Рис. 46

В качестве элементарной массы выберем часть этого стержня массой dm, длиной dx, расположенную на расстоянии х от середины стержня. Тогда можем записать:

,

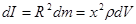здесь 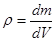- объемная плотность стержня., .

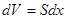Плотность можно найти следующим образом:

,

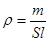где S – площадь поперечного сечения стержня.

Момент инерции всего стержня рассчитаем следующим образом:

.

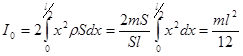Сразу же можно получить момент инерции стержня относительно оси, проходящей через конец стержня перпендикулярно ему.

.

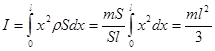1. Момент инерции диска массой m радиусом R относительно оси, проходящей через его центр масс перпендикулярно ему.

Как показано на рис. 47, в качестве элементарной массы удобно выбирать кольцо радиусом r и толщиной dr.

Рис. 47

Найдем момент инерции этой элементарной массы:

,

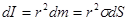здесь 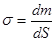- поверхностная плотность диска, 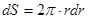- элемент площади кольца.

Поверхностную плотность диска можно найти следующим образом:

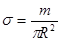
Тогда момент инерции всего диска равен:

.

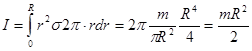3.Теорема Штейнера

В некоторых случаях, зная момент инерции тела относительно оси, проходящей через центр масс тела, можно легко найти моменты инерции относительно некоторых других осей. Проведем ось 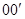через центр масс тела, другая ось 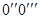, проходит параллельно первой через точку (х₀, у₀) на расстоянии 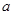(рис. 48).

Рис. 48

Можем записать, что:

.

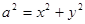Рассмотрим элементарную массу тела 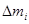с координатами 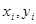. Ее момент инерции относительно оси, проходящей через начало координат равен:

.

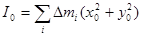Найдем момент инерции тела относительно параллельной оси:

.

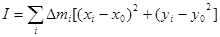Выполним действия в скобках:

.

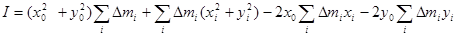Последние два слагаемых обращаются в нуль, т.к. они представляют собой координаты центра масс в системе центра масс. Тогда имеем:

.

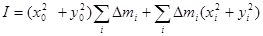Первое слагаемое представляет собой произведение массы тела на квадрат расстояния 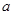между осями, второе слагаемое есть момент инерции тела относительно оси, проходящей через центр масс. Итак, теорема Штейнера:

.

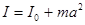Момент инерции тела относительно некоторой оси равен сумме момента инерции тела относительно оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями, если эти оси параллельны.

4.Связь между моментами инерции плоской фигуры.

Получим еще одну полезную для расчетов моментов инерции формулу. Рассмотрим плоское тело, расположенное в плоскости х,у (рис. 49).

Рис. 49

Выберем элементарную массу 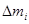этого тела на расстоянии 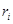от начала координат. Тогда можем записать:

.

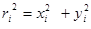Момент инерции этой элементарной массы относительно оси z равен:

.

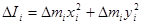Просуммировав по всему телу, получим момент его инерции относительно оси z:

.

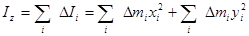Иначе это можно записать:

.

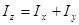Применим эту формулу для расчета момента инерции диска массой m и радиуса R относительно оси, лежащей в плоскости диска, и проходящей через его центр масс (рис. 50)::

Рис. 50

Мы нашли момент инерции такого диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс:

.

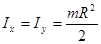Теперь можем записать:

.

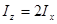Отсюда следует, что:

.

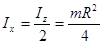5.Уравнение динамики твердого тела, вращающегося вокруг неподвижной оси.

Найдем производную по времени правой и левой части уравнения

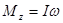
Получим:

,

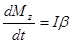здесь 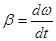- угловое ускорение твердого тела.

Используя закон изменения момента импульса:

,

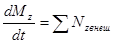можем получить уравнение динамики твердого тела, вращающегося вокруг неподвижной оси:

= .

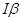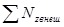Если суммарный момент внешних сил равен нулю ( 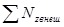=0), то выполняется закон сохранения момента импульса твердого тела относительно оси:

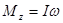= const.

Вращение твердого тела вокруг некоторой оси с постоянным моментом импульса аналогично поступательному движению тела по инерции. Однако, существуют и некоторые различия. При движении по инерции масса тела остается постоянной, а при вращении вокруг оси момент инерции тела может изменяться, но при этом будет изменяться и угловая скорость вращения так, что 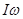= const. Этот закон используют, например, фигуристы при вращении вокруг оси резко меняя расположение отдельных частей тела, они резко увеличивают угловую скорость вращения.

Для тела произвольной формы вектор суммарного момента импульса относительно начала 0 не совпадает с направлением вектора угловой скорости вращения тела (рис. 51).

Рис. 51

Он поворачивается вместе с телом вокруг оси вращения.

Для симметричного тела эти векторы совпадают и можно записать следующее выражение в векторном виде:

.

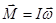Ось, положение которой в пространстве не изменяется при вращении твердого тела, называется свободной осью тела.

В теории доказывается, что для тела произвольной формы существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые являются свободными осями. Эти оси называют главными осями инерции тела.

Например, у цилиндра в качестве одной главной оси можно выбрать оси его симметрии, а качестве двух других могут быть выбраны две любые взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной оси цилиндра.

Момент инерции тела относительно главных осей называют главными моментами инерции тела. При вращении тела, устойчивым является его вращение вокруг главных осе, соответствующих максимальному и минимальному значению момента инерции (хорошо видно на вращении коробка спичек при свободном падении).

5.Кинетическая энергия вращающегося твердого тела (на самостоятельное изучение).

Рассмотрим некоторое твердое тело, вращающееся вокруг неподвижной оси с угловой скоростью 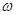. Раз объем это тело на элементарные массы 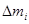и запишем ее кинетическую энергию. Поскольку для модуля линейной скорости точки, вращающейся по окружности, справедливо соотношение:

,

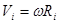то можем далее записать:

.

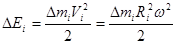Просуммировав по всем материальным точкам твердого тела, получим:

.

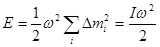Здесь I –момент инерции твердого тела относительно некоторой оси z.

Найдем работу, совершаемую при вращательном движении твердого тела. По теореме об изменении кинетической энергии можем записать:

,

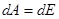Здесь А – работа всех сил, действующих на тело.

Тогда имеем:

.

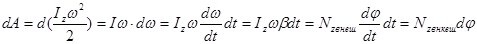Здесь N_zвнеш - суммарный момент внешних сил, действующих на тело, 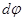- элементарный угол поворота.

Можем составить следующую таблицу аналогий поступательного и вращательного движения.

Поступательное движение	Вращательное движение
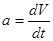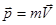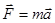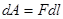
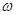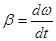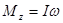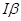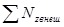Линейная скорость – V Линейное ускорение - Масса - m Сила - F Импульс – Уравнение поступательного движения - Работа при поступательном движении -	Угловая скорость - Угловое ускорение - Момент инерции – I Момент силы – М Момент импульса - Уравнение вращательного движения - = . Работа при вращательном движении -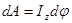

В качестве примера рассчитаем кинетическую энергию катящегося с постоянной скоростью V по горизонтальной поверхности диска массой m, радиуса R.

По теореме Кенига кинетическую энергию диска можем записать в виде суммы кинетической энергии поступательного движения диска со скоростью центра масс и кинетической энергии вращательного движения относительно оси, проходящей через центр масс:

.

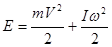Поскольку диск движется без проскальзывания, то линейная скорость точек на его ободе равна по модулю скорости поступательного движения центра масс:

.

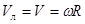Подставляя это в первое выражение, получим:

.

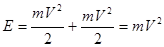6.Применение уравнения вращательного движения к решению некоторых задач: скатывание тел с наклонной плоскости, маятник Максвелла, физический маятник.

Рассмотрим скатывание без скольжения цилиндра массой m и радиуса R с наклонной плоскости (рис. 52).

Рис. 52

В данном случае сила Т (сила трения) есть сила , которая обеспечивает движение цилиндра без проскальзывания. Напишем уравнение поступательного движения центра масс цилиндра и уравнение его вращательного движения относительно оси, проходящей через точку 0:

.

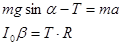Добавим сюда еще кинематическую связь углового и линейного ускорения:

.

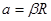Решив эту систему трех уравнений с тремя неизвестными, получим величину ускорения центра масс:

.

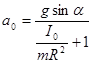Подставив для момента инерции цилиндра 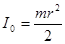, получим .

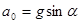Б) Маятник Максвелла.

В качестве второго примера рассмотрим диск массой m, с радиусом его оси R₀, подвешенный на двух нитях, намотанных на его ось (рис.53).

Рис. 53

Запишем уравнение поступательного движения его центра масс, уравнение вращательного движения относительно оси, проходящей через центра масс и кинематическую связь:

.

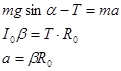Мы получили точно такую же систему, как и в прошлой задаче и, следовательно, решение будет иметь такой же вид:

.

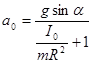При достаточно малом моменте инерции (в пределе при 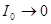) видим, что диск падает, как свободное тело ( 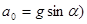. При этом сила натяжения нити .

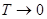В) Физический маятник.

Физическим маятником называется любое тело, которое может совершать колебания относительно некоторой оси. Запишем уравнение его вращательного движения относительно точки подвеса 0 ( рис.54):

,

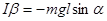где 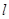- расстояние от оси вращения до центра тяжести.

Рис. 54

Знак минус в этом уравнении означает, что при колебаниях физического маятника момент сил относительно точки подвеса направлен противоположно увеличению угла отклонения 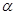. Рассмотрим, так называемые, малые колебания физического маятника. В этом случае можно записать, что 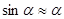с достаточной большой степенью точности. Тогда наше уравнение принимает вид:

.

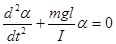Величина 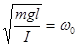называется частотой собственных колебаний физического маятника, а период его колебаний равен:

.

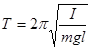7.Трение качения.

Движение абсолютно твердого тела по абсолютно твердой поверхности должно продолжаться бесконечно долго, т.к. нет сил, препятствующих такому движению. В реальности такое движение не может продолжаться бесконечно. Качение рано или поздно прекратится. При этом механическая энергия движения цилиндра переходит во внутреннюю энергию взаимодействующих тел. Этот процесс можно объяснить существованием особой силы трения – трения качения. При качении, например, цилиндра, он и поверхность деформируются (рис.55).

Рис. 55

Если эти деформации упруги, то силы взаимодействия между цилиндром и поверхностью будут симметричны относительно вертикальной плоскости 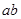, проходящей через ось цилиндра. Результирующая всех сил упругой деформации поверхности будет вертикальна, и момент этих сил относительно оси цилиндра также будет равен нулю. Никаких сил трения качения в этом случае не возникает.

Следовательно, для объяснения сил трения качения следует считать деформации цилиндра и плоскости неупругими. При неупругой деформации поверхности силы, действующие на цилиндр со стороны плоскости уже не будут симметричны относительно плоскости 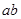. Поэтому равнодействующая всех этих сил обязательно будет иметь горизонтальную составляющую, направленную назад, и момент этих сил относительно оси цилиндра также не равен нулю.

Установим, где должна проходить составляющая всех сил реакции поверхности (рис. 56).

Рис. 56

Точка приложения равнодействующей не может быть расположена ни в вертикальной плоскости 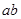, проходящей через центр, ни сзади нее, ибо тогда эта сила сообщила бы положительное угловое ускорение цилиндру. Следовательно, точка приложения силы N должна находиться впереди, причем линия силы N должна проходить выше центра цилиндра, в противном случае она сообщала бы цилиндру положительное ускорение. Таким образом, сила взаимодействия цилиндра с поверхностью расположена так, как показано на рис. 56в.

Горизонтальная компонента силы N представляет собой силу трения качения f. Обычно в таблицах дают значения величины s и говорят не о силе трения качения:

,

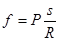где Р – сила тяжести, а R –радиус цилиндра, а о моменте силы трения качения:

.

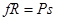Расстояние s называют коэффициентом момента силы трения качения. Величина s зависит только от материала цилиндра и плоскости.

8.Уравнение плоского движения твердого тела.

Рассмотрим плоское движение твердого тела относительно неподвижной системы координат, не принадлежащей этому телу. Допустим, что на некоторую элементарную массу 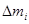этого тела, заданную относительно начала отсчета 0 с помощью радиус-вектора 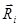, действуют внешние и внутренние силы 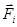. Запишем уравнение поступательного движения этой элементарной массы:

.

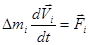Умножим это уравнение векторно на радиус-вектор частицы :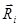

.

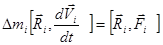Просуммируем это выражение по всем элементарным частицам тела:

.

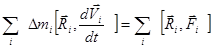Рассмотрим формально следующее выражение:

.

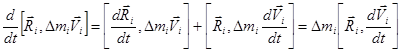Первое слагаемое обратилось в нуль по свойству векторного произведения. Тогда предыдущее выражение запишем, как:

.

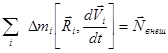Или иначе:

.

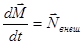Мы получили основной закон динамики плоского движения твердого тела:

Момент всех внешних сил равен скорости изменения момента импульса твердого тела относительно любой неподвижной точки.

Внешне это уравнение похоже на закон динамики твердого тела, вращающегося вокруг неподвижной оси:

.

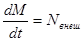Однако, в последнем законе фигурирует момент импульса тела относительно оси, а в первом – момент импульса относительно точки.

9.Тензор инерции.

Ранее, рассматривая вращение твердого тела вокруг неподвижной оси, мы получили соотношение между моментом импульса этого тела относительно оси и угловой скоростью 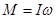, здесь I –момент инерции тела относительно оси вращения. Для однородного симметричного тела векторы 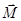и 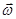коллинеарные, и это уравнение можно записать в векторной форме :

.

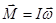Аналогичное соотношение можно получить и для тела произвольной формы.

Момент импульса элементарной массы такого тела относительно точки начала отсчета 0 можно записать в следующем виде:

.

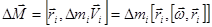Двойное векторное произведение раскрывается следующим образом:

.

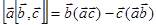Тогда имеем:

.

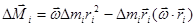Просуммируем по всем элементарным массам твердого тела:

.

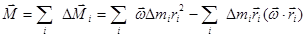Найдем проекции момента импульса твердого тела относительно оси на оси декартовой системы координат, связанной с этим началом 0:

.

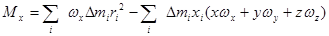Или после простых преобразований:

.

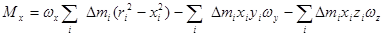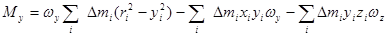
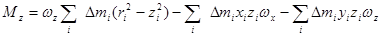
Введем следующие обозначения:

.

.

.

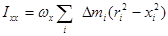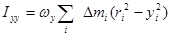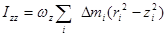Назовем их осевыми моментами инерции.

.

.

.

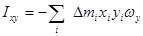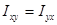
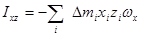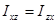
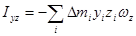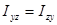
Назовем эти величины центробежными моментами инерции.

В самом общем случае связь между компонентами вектора момента импульса относительно точки и компонентами вектора угловой скорости может быть записана в следующем виде:

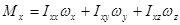
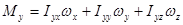
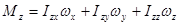
Совокупность девяти величин 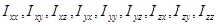, связывающих векторы момента импульса и угловой скорости между собой, называют тензором инерции. Тензор принято записывать в виде таблицы:

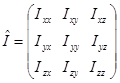
Расположенные по диагонали компоненты называют диагональными компонентами тензора. Они являются осевыми моментами инерции. Недиагональные компоненты тензора являются центробежными моментами инерции.

Таким образом, в общем случае можем записать:

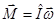
Ранее, рассматривая вращение твердого тела вокруг неподвижной оси, мы ввели понятие главных осей инерции тела произвольной формы. Если в качестве координатных осей выбрать главные оси инерции тела, то центробежные моменты инерции обращаются в нуль и тензор инерции принимает следующий вид:

.

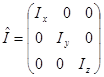Величины 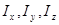называют главными моментами инерции тела (это осевые моменты, вычисленные не в произвольных, а в главных осях).

10.Гироскопы.

Гироскопом называется массивное симметричное тело, быстро вращающееся вокруг оси симметрии. Поскольку ось гироскопа это одна из его главных осей инерции, то при вращении сохраняется ее направление в пространстве. Для демонстрации свойств гироскопа в лабораторных условиях используется карданов подвес (рис. 57).

Рис. 57

Гироскоп в кардановом подвесе имеет три степени свободы и может совершать любые повороты вокруг центра подвеса. Если привести гироскоп в кардановом подвесе в быстрое вращение, то при любом повороте подставки ось его вращения сохраняет неизменным свое направление в пространстве. Это явление называется гироскопическом эффектом.

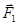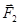Пусть на ось вращающегося гироскопа действуют силы и , перпендикулярные плоскости рис. 58.

Рис. 58

Момент этих сил 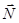направлен вдоль оси 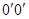. Действие этого момента сил в течение времени dt приведет к изменению момента импульса гироскопа 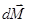, что даст новый момент импульса 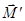, лежащий в плоскости рисунка. Направление этого вектора задает новое направление оси вращения гироскопа. Таким образом, ось вращения гироскопа повернется на угол 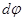. Поворот оси вращения гироскопа в новое положение произошел с угловой скоростью 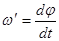. Таки образом, действие момента сил на ось гироскопа приводит к ее повороту в плоскости, перпендикулярной плоскости действия сил. Если же внешние силы действуют постоянно, то ось гироскопа будет вращаться с угловой скоростью 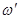. Такое движение оси называется прецессией, а величина 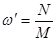называется угловой скоростью прецессии.

Описанные свойства гироскопа находят некоторые практические применения. Например, существует прибор, называемый гирокомпасом, который представляет собой гироскоп, ось которого может свободно поворачиваться в горизонтальной плоскости. Под влиянием суточного вращения Земли ось гироскопа устанавливается в такое положение, при котором угол между этой осью и осью вращения земли будет минимальным. В этом положении ось гироскопа указывает точно на север.

ОСНОВЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ

Релятивистская динамика

1. Специальная теория относительности.

В основе классической механики Ньютона заложены два постулата:

1. Принцип относительности механического движения Галилея – никакими механическимиопытами нельзя отличить состояние покоя от состояния равномерного прямолинейного движения или все механические явления протекают одинаково во всех инерциальных системах отсчета.
2. Постоянство времени в различных инерциальных системах отсчета – время во всех системах отсчета течет одинаково.

Однако в конце XIX века в физике назрел кризис, связанный с тем, что появившиеся к тому времени уравнения электромагнитного поля Максвелла не удовлетворяют преобразованиям координат Галилея. Система уравнений Максвелла не инвариантна относительно этих преобразований, в то время, как законы Ньютона этим преобразованиям удовлетворяют. Оказалось, что существуют ограничения действий уравнений Ньютона – они описывают движение со скоростями, гораздо меньшими скорости света, т.е. случай 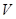<< с.

Для выхода из этого кризиса Альберт Эйнштейн в 1905 г. создал специальную теорию относительности (СТО), в основе которой лежат два постулата:

1. Принцип относительности Эйнштейна - все законы природы одинаковы во всех инерциальных системах отсчета.
2. Постоянство скорости света - скорость света в вакууме не зависит от движения источников света и, следовательно, одинакова во всех инерциальных системах отсчета.

Второй постулат приводит нас к новым понятиям об относительности пространства и времени. Из него вытекают относительность промежутков времени и расстояний.

2.Преобразование времени и длины в движущихся системах отсчета.

Рассмотрим следующий мысленный опыт, показанный на рис. 59.

Рис. 59

Имеем некоторые условные часы, которые издают звуковой сигнал при попадании света на приемник. На концах вертикального стержня длиной 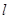закреплены горизонтально два параллельных зеркала. Световой импульс от источника движется между зеркалами, поочередно отражаясь от них. Если прибор находится в неподвижной системе координат, часы будут издавать звуковой сигнал через интервал времени 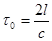. Пусть теперь часы идут в системе отсчета, которая движется влево со скоростью V. Как видно из рисунка, часы будут издавать сигнал через интервал времени:

.

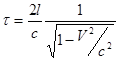Окончательно получаем:

.

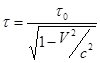Видно, что в движущихся системах отсчета время течет медленнее, чем в неподвижных Этот эффект называют релятивистским замедлением времени. Причина замедления времени – второй постулат Эйнштейна о постоянстве скорости света.

Рассмотрим теперь другой опыт. Расположим стержень длиной 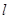в неподвижной системе отсчета вдоль оси х (рис. 60).

Рис. 60

В неподвижной системе отсчета длина стержня равна 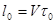, в движущейся системе отсчета длина этого же стержня равна 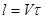. Используя связь между временем в неподвижной и в движущейся системе отсчета, получим:

.

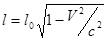Длина стержня зависит от системы отсчета – все тела сжимаются в направлении движения.

3.Преобразования Лоренца.

Полученные выше соотношения позволяют получить релятивистский закон преобразования координат и времени в инерциальных системах отсчета.

Рассмотрим отрезок ОВ длиной 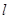, неподвижный в системе отсчета К (рис. 61).

Рис. 61

Связь между длинами в подвижной и неподвижной системе имеет вид:

.

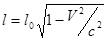Тогда можем записать:

.

Откуда следует:

.

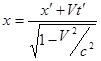В этой формуле можно сделать замену 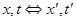. Тогда получим:

.

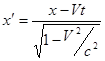Для двух других координат имеем:

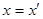
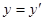
Найдем теперь преобразование времени. Можем записать:

.

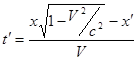В свою очередь 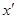выражается через 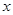и .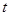

.

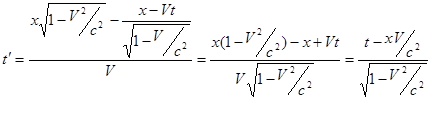Можно получить обратный переход:

.

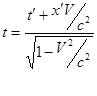Таким образом, мы имеем набор формул для релятивистских преобразований координат и времени:

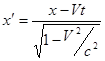
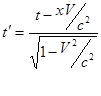
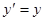
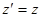
Эти преобразования называют преобразованиями Лоренца. Они заменяют преобразования Галилея при релятивистских скоростях.

4.Закон сложения скоростей в релятивистской динамике.

Для релятивистских движений закон сложения скоростей отличается от закона сложения скоростей Галилея. Рассмотрим опять две системы отсчета – неподвижную систему 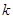и движущуюся относительно нее с постоянной скоростью V систему 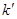. Пусть в системе 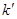частица смещается на 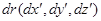. Следовательно, в этой системе скорость частицы равна .

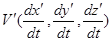Согласно преобразованиям Лоренца можем записать:

.

.

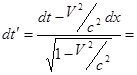
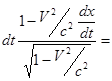
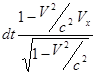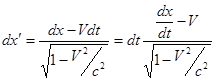Найдем скорость частицы в движущейся системе отсчета:

.

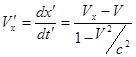Аналогично найдем и другие компоненты скорости:

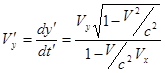
&nb