Силы сухого трения (трение покоя и трение скольжения).

Сухое трение возникает на поверхностях соприкосновения твердых тел. При этом различают два вида трения: трение покоя и трение скольжения.

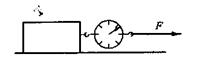Подействуем некоторой силой F на тело, лежащее на горизонтальной поверхности (рис.12).

Рис.12

Опыт показывает, что пока сила F меньше некоторого критического значения F_кр тело покоится относительно поверхности. Расставим силы, действующие на тело, на рис. 13.

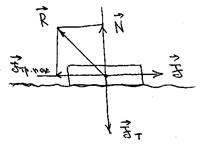
Рис. 13

Поскольку тело взаимодействует с тремя телами (внешним, с Землей и поверхностью), на него действуют три силы: внешняя 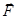, сила тяжести Земли 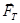и сила взаимодействия с поверхностью 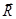. Теперь можно предложить следующую модель взаимодействия тела с поверхностью. С одной стороны, тело под действием силы тяжести давит на поверхность, деформирует ее и вызывает появление ответной силы – силы упругой реакции поверхности 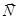. С другой стороны, поверхность и тело шероховаты и между ними есть взаимодействие, которое описывается силой трения 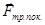. Эта сила называется сила трения покоя, т.к. тело покоится относительно поверхности. Формулы для расчета силы трения покоя не существует, т.к. она равна по модулю внешней силе, ее уравновешивающей.

Рассмотрим тело, покоящееся на наклонной плоскости (рис.14).

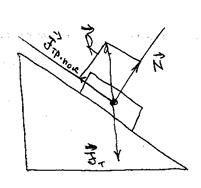Рис. 14

На него также действуют только две силы: сила тяжести 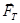и сила взаимодействия с наклонной плоскостью 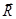. Эту силу представим как равнодействующую двух сил: силы упругой реакции наклонной плоскости 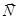и силу трения покоя .

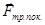Обратимся опять к рис.13. Когда внешняя сила превышает критическое значение F_кр, то тело начинает скользить по поверхности и появляется сила трения скольжения 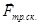. При специальной обработке поверхностей сила трения скольжения практически не зависит от скорости, и ее величина определяется выражением:

= .

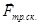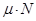Здесь 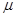- коэффициент трения скольжения, N- сила упругой реакции опоры.

Опыт показывает следующий вид зависимости силы трения от скорости движения тела, который приведен на рис. 15.

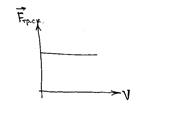Рис. 15

Этот закон иногда называют законом Кулона - Амонтона.

2.Вязкое трение.

При движении тела в вязкой среде, на него действуют силы вязкого трения. Например, при движении шарика массой m в вязкой жидкости на него действуют три силы: сила тяжести, сила вязкости и выталкивающая сила (сила Архимеда). Как показывают опыты, при небольших скоростях силы вязкости подчиняются закону:

,

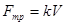здесь k –некий коэффициент пропорциональности.

Уравнение движения имеет вид:

.

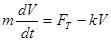Это дифференциальное уравнение с разделяющимися переменными можно привести к виду:
.

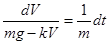Решаем это уравнение путем интегрирования правой и левой его части:

.

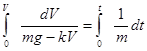В результате получим:

.

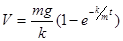Видим, что движение тела в вязкой среде является сложным: в начальный момент времени оно ускоренное. Затем ускорение будет уменьшаться и через некоторое время станет практически равным нулю – движение будет близко к равномерному. Время установления равномерн6ого движения зависит от коэффициента пропорциональности k.