Кинематика движения материальной точки по окружности

Рассмотрим движение материальной точки по окружности радиуса R. Если движение происходит с постоянной по модулю скоростью, то можно ввести понятие периода Т, как времени, за которое тело совершает один полный оборот. Число оборотов 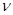в единицу времени называют частотой 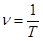. Далее можно ввести понятие угловой скорости вращения по окружности (см. рис. 9):

.

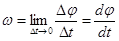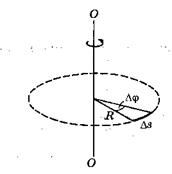Рис. 9

Если угловая скорость изменяется, то вводится угловое ускорение 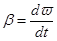. Можно найти связь между угловой и линейной скоростью движения по окружности. Модуль линейной скорости равен:

.

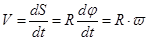Найдем общую связь между векторами угловой и линейной скорости. Введем понятие вектора угловой скорости 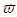- следующим образом – это вектор, направленный по оси вращения по правилу правого винта, а его модуль равен производной угла поворота по времени. Рассмотрим рис. 10, где положение точки на окружности описывается с помощью радиус-вектора .

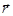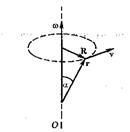Рис. 10

Рассмотрим формально следующее векторное произведение:

.

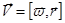Его модуль равен 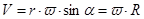, а направлен он по оси вращения. Таким образом, это и есть общая связь векторов угловой и линейной скорости.