Импульс частицы и системы частиц
1. Импульс частицы. Закон изменения импульса частицы.
Огромную роль в изучении физических явлений играют, так называемые сохраняющиеся величины. Одной из них является импульс частицы. Вспомним, что импульсом частицы называется векторная физическая величина 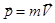 . Именно эта величина входит во второй закон Ньютона:
. Именно эта величина входит во второй закон Ньютона:
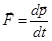 .
.
Отсюда следует следующее выражение 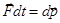 . В правой части стоит приращение импульса частицы, а величина, стоящая в левой части, называется импульс силы. Видно, что при движении частицы, ее импульс (т.е. ее скорость) может изменить не сама сила, а ее импульс. В частности, для постоянной силы можем записать
. В правой части стоит приращение импульса частицы, а величина, стоящая в левой части, называется импульс силы. Видно, что при движении частицы, ее импульс (т.е. ее скорость) может изменить не сама сила, а ее импульс. В частности, для постоянной силы можем записать 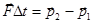 .
.
2. Импульс системы частиц.
Рассмотрим систему N материальных точек, на которую действуют некоторые силы. Разделим эти силы на две группы: 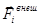 - внешние силы, действующие на i -ю частицу и
- внешние силы, действующие на i -ю частицу и 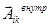 - внутренние силы взаимодействия частиц между собой.
- внутренние силы взаимодействия частиц между собой.
Запишем закон изменения импульса 1-ой частицы:
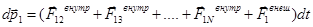 .
.
Запишем закон изменения импульса 2-ой частицы:
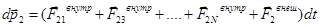 .
.
Запишем закон изменения импульса i-ой частицы:
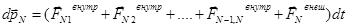 .
.
Величину, стоящую в левых скобках 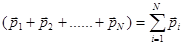 , назовем суммарным импульсом
, назовем суммарным импульсом 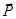 системы материальных точек. Рассмотрим более подробно правую часть этого выражения. Видно, что в нее входят выражения типа:
системы материальных точек. Рассмотрим более подробно правую часть этого выражения. Видно, что в нее входят выражения типа: 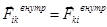 , которые по третьему закону Ньютона равны по модулю и противоположны по направлению. Все такие суммы равны нулю, в итоге имеем:
, которые по третьему закону Ньютона равны по модулю и противоположны по направлению. Все такие суммы равны нулю, в итоге имеем:
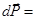
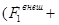
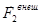 +………+
+………+ 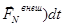 .
.
Это выражение представляет собой закон изменения импульса системы, взаимодействующих между собой частиц – изменение импульса такой системы частиц равно суммарному импульсу всех внешних сил, действующих на систему. Отсюда следует очень важный практический вывод: импульс системы частиц может изменяться только под действием внешних сил.
Назовем замкнутой такую систему частиц, на которую не действуют внешние силы. Тогда сформулируем закон сохранения импульса:
В замкнутых системах суммарный импульс остается постоянным.
Замечание.
У незамкнутых систем может сохраняться постоянной какая-либо проекция импульса.
3. Центр масс системы частиц. Закон движения центра масс системы.
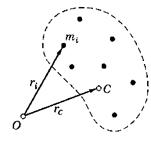 Рассмотрим систему N материальных точек, заданных в пространстве с помощью радиус-векторов
Рассмотрим систему N материальных точек, заданных в пространстве с помощью радиус-векторов 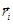 (рис. 24).
(рис. 24).
Рис. 24
На эту систему действуют внешние силы, под действием которых она может перемещаться. Для такой системы можно вести некоторую точку пространства, не обязательно совпадающую с какой-либо из точек системы, которая обладает рядом интересных свойств. Введем точку С при помощи следующего радиус-вектора:
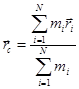 .
.
Здесь mi – масса i-ой частицы.
Полученную таким образом точку называют центром масс системы частиц.
Найдем производную по времени от этого выражения:
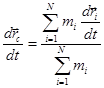 .
.
Здесь 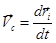 - представляет собой скорость движения центра масс системы частиц. Или перепишем это соотношение несколько иначе:
- представляет собой скорость движения центра масс системы частиц. Или перепишем это соотношение несколько иначе:
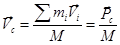 .
.
Мы обозначили 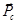 - импульс системы частиц, M – суммарная масса всей системы.
- импульс системы частиц, M – суммарная масса всей системы.
Вспомним уравнение движения системы материальных точек под действием внешних сил:
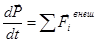 .
.
Выразив 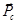 из предыдущего уравнения и подставив результат сюда, получим:
из предыдущего уравнения и подставив результат сюда, получим:
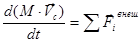 .
.
Или иначе:
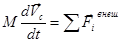 .
.
Обозначим 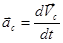 - ускорение центра масс системы частиц, получим закон движения центра масс:
- ускорение центра масс системы частиц, получим закон движения центра масс:
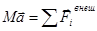 .
.
Центр масс системы движется, как точка с массой, равной всей массе системы, под действием результирующей всех внешних сил, действующих на эту систему.
Закон движения центра масс системы:
если система замкнута, то ее центр масс либо покоится, либо движется прямолинейно и равномерно.
Задачи по теме.
- На дне закрытой пробирки сидит муха. Пробирка свободно падает, оставаясь в вертикальном положении. Как изменится продолжительность падения, если во время падения муха перелетит из нижней части пробирки в верхнюю?
- На гладком горизонтальном столе находится сосуд массой М, который разделен непроницаемой перегородкой на две равные части. В левой части сосуда находится газ массой 2м, а в правой – газ массой 3м. Куда и на сколько сместится сосуд, если перегородку внезапно удалить?
V. Энергия частицы и системы частиц.
1. Механическая работа.
Пусть на частицу в точке А действует некоторая сила 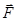 , при этом она проходит элементарный путь
, при этом она проходит элементарный путь 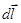 (рис. 25).
(рис. 25).
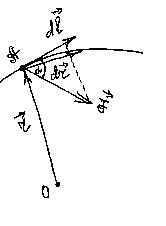 |
Рис. 25
Здесь вектор 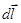 (иначе еще его называют элементом траектории) направлен по касательной к траектории в точке А и по модулю равен пути ds, пройденному точкой вдоль траектории. Заметим, что эта величина не совпадает с элементарным перемещением
(иначе еще его называют элементом траектории) направлен по касательной к траектории в точке А и по модулю равен пути ds, пройденному точкой вдоль траектории. Заметим, что эта величина не совпадает с элементарным перемещением 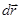 точки А. При таком перемещении сила
точки А. При таком перемещении сила 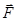 остается постоянной.
остается постоянной.
Назовем элементарной работой силы следующую величину:
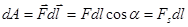 .
.
Здесь 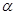 - угол между вектором силы и элементом траектории, а
- угол между вектором силы и элементом траектории, а 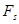 - проекция вектора силы на направление вектора
- проекция вектора силы на направление вектора 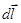 .
.
Если же сила изменяется при движении очки вдоль траектории, то работа в этом случае находится как сумма всех элементарных работ:
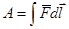 .
.
2. Центральные силы. Работа гравитационных сил
Центральной силой называется такая сила, которая зависит только от расстояния до некоторого центра О и всегда направлена по радиус-вектору движущейся точки относительно этого центра. В качестве примера такой силы рассмотрим силу гравитационного притяжения двух материальных точек массами m1 и m2 (рис. 26).
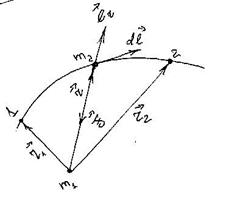 |
Рис. 26
Найдем работу такой силы при перемещении частицы массой m2 из точки 1 в точку 2. Сила гравитационного взаимодействия имеет вид :
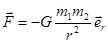 .
.
Элементарная работа этой силы
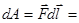
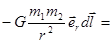
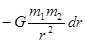 .
.
Внимание, здесь dr есть приращение модуля радиус-вектора 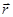 , а не модуль перемещения.
, а не модуль перемещения.
Ищем теперь работу силы на всем пути частицы от точки 1 до точки 2:
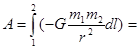
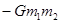
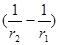 .
.
3. Кинетическая энергия. Теорема об изменении кинетической энергии.
Если на тело действует некоторая сила 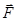 , под действием которой тело совершает перемещение
, под действием которой тело совершает перемещение 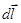 , то говорят , что сила совершает работу. Рассмотрим сначала одномерный случай движения тела под действием силы Fх вдоль оси Х.. Запишем
, то говорят , что сила совершает работу. Рассмотрим сначала одномерный случай движения тела под действием силы Fх вдоль оси Х.. Запишем
уравнение движения тела для этого случая:
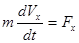 .
.
Умножим это уравнение слева и справа на величину перемещения dx .
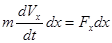 .
.
Получим далее:
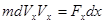 .
.
Рассмотрим выражение: 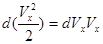 . Можем теперь записать:
. Можем теперь записать:
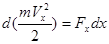 .
.
Выражение в правой части есть элементарная работа dA, а выражение, стоящее в левой части, есть приращение некоторой физической величины Е. Эту величину Е= 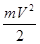 назовем кинетической энергией тела. Кинетическая энергия тела это энергия его движения, следовательно ее нельзя запасать. Это выражение может быть обобщено на движение по траектории любого типа и, следовательно, получим общее выражение:
назовем кинетической энергией тела. Кинетическая энергия тела это энергия его движения, следовательно ее нельзя запасать. Это выражение может быть обобщено на движение по траектории любого типа и, следовательно, получим общее выражение:
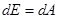 .
.
Мы получили теорему об изменении кинетической энергии тела:
Приращение кинетической энергии тела равно работе всех сил, совершающих работу.
4.Консервативные силы. Поле центральных сил.
Если с каждой точкой пространства связана некоторая векторная величина, то говорят, что задано поле этой физической величины. Например, может быть задано поле сил тяжести и т.д. Если при перемещении частицы в некотором силовом поле работа не зависит от формы траектории, а только от начальной и конечной точки, то такое поле называется консервативным или потенциальным. Пусть в консервативном поле тело из точки 1 перемещается в точку 2 по произвольной траектории (рис. 27).
а 

 1
1
в
Рис. 27
Можно сформулировать свойство консервативности сил несколько иначе. Рассмотрим перемещение тела на замкнутом пути 1а2в1. Работа при этом может быть записана как:
А=А1а2 + А2в1.
Можно увидеть, что из определения работы силы следует, что А2в1 = - А1в2 . Поэтому
А = А1а2 – А1в2 .
Работа в консервативном поле не зависит от формы траектории, следовательно А=0. Получаем, что работа по замкнутому контуру в поле консервативных сил равна нулю.
5.Поле центральных сил
Мы уже давали определение центральных сил. Рассмотрим теперь работу в поле таких сил. Общий вид центральной силы может быть записан следующим образом (рис.28):
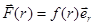 .
.
Здесь 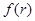 - модуль центральной силы,
- модуль центральной силы, 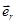 - единичный вектор направления
- единичный вектор направления 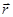 .
.
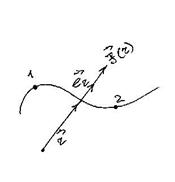 |
Рис. 28
Найдем работу этой силы на некотором пути из точки 1 в точку 2. По определению полной работы:
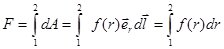 .
.
Здесь 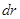 , как было показано выше, модуль приращения вектора перемещения. Видно, что эта работа не зависит от формы траектории, а только от положения начальной и конечной точки и, естественно, от вида функции
, как было показано выше, модуль приращения вектора перемещения. Видно, что эта работа не зависит от формы траектории, а только от положения начальной и конечной точки и, естественно, от вида функции 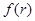 . Следовательно, центральные силы являются консервативными.
. Следовательно, центральные силы являются консервативными.
5. Потенциальная энергия частицы в поле сил.
Воспользуемся тем фактом, что работа консервативных сил не зависит от формы траектории, и введем новое физическое понятие потенциальной энергии частицы.
Рассмотрим поле консервативных сил, в котором частица совершает несколько последовательных независимых перемещений из некоторой начальной точки О в точки 1, 2 и 3 (рис. 29).
 1 2 3
1 2 3

Рис. 29
Так в консервативном поле работа не зависит от пути, то в данном случае работа зависит только от положения конечных точек пути 1,2 и 3. Данная работа будет некоторой функцией  радиус-вектора частицы, проведенного из точки 0. Эту функцию и назовем потенциальной энергией частицы в произвольной точке пространства относительно начальной точки 0. Введем эту функцию по следующему правилу:
радиус-вектора частицы, проведенного из точки 0. Эту функцию и назовем потенциальной энергией частицы в произвольной точке пространства относительно начальной точки 0. Введем эту функцию по следующему правилу:
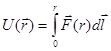 .
.
Найдем теперь работу консервативных сил при перемещении частицы из точки 1 непосредственно в точку 2, минуя точку 0.
А12 = А10 + А 02.
Это выражение запишем иначе:
А12 = U1 - U2.
Итак, потенциальной энергией частицы в поле консервативных сил называют такую функцию 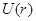 , убыль которой равна работе по перемещению частицы из одной точки пространства в другую. Видно, что введенная таким образом величина, является понятием относительным.
, убыль которой равна работе по перемещению частицы из одной точки пространства в другую. Видно, что введенная таким образом величина, является понятием относительным.
6.Потенциальная энергия и сила поля.
В динамике при описании поведения частиц мы использовали понятие силы и второй закон Ньютона. Оказывается, что поведение частицы в консервативном поле можно описать на основе понятия потенциальной энергии.
Установим связь между потенциальной частицей в консервативном поле и силой, действующей на частицу в этом поле. Для элементарной работы можем записать:
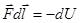 .
.
Или иначе 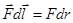 , тогда
, тогда 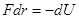 . Отсюда следует, что
. Отсюда следует, что
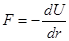 .
.
В общем случае существует следующая связь силы с изменением потенциальной энергии:
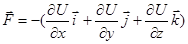 .
.
В скобках стоит некий оператор (набла), который еще иначе называют градиентом (grad): 
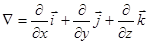 .
.
Поэтому связь силы и потенциальной энергии можно записать более компактно:
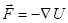 .
.
7. Механическая энергия частицы.
Закон изменения и сохранения механической энергии частицы.
Рассмотрим частицу, находящуюся в поле консервативных сил. Тогда все силы, действующие на частицу, можно разбить на две группы: силы, действующие на частицу со стороны этого поля и силы, не принадлежащие к этому полю (они могут быть как консервативными, так и диссипативными). Эти вторые силы назовем сторонними. Система, на которую действую сторонние силы, называют незамкнутой.
Как известно, все силы, действующие на частицу, изменяют ее кинетическую энергию:
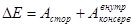 .
.
С другой стороны, известно что:
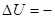
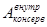 .
.
Тогда первое уравнение принимает вид:
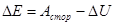 .
.
Перепишем его иначе:
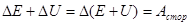 .
.
Величину, стоящую в скобках, назовем механической энергией частицы: 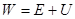 .
.
Мы получили закон изменения механической энергии частицы:
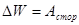 .
.
Приращение механической энергии частицы равно работе сторонних сил, действующих на эту частицу.
Соответственно, можно сформулировать и закон сохранения механической энергии частицы:
В случае отсутствия сторонни сил, механическая энергия системы сохраняется.
8. Применение закона сохранения механической энергии частицы к анализу ее движения в консервативных полях.
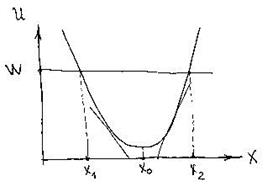 Рассмотрим одномерное движение частицы вдоль оси Х, если известен вид зависимости потенциальной энергии от координаты частицы (рис.30):
Рассмотрим одномерное движение частицы вдоль оси Х, если известен вид зависимости потенциальной энергии от координаты частицы (рис.30):
Рис. 30
Поскольку сторонних сил нет, то выполняется закон сохранения механической энергии частицы W=E+U=const. Поскольку кинетическая энергия всегда больше нуля, то следует очевидное условие: W>U. Выберем некоторое значение механической энергии частицы (ему соответствует горизонтальная линия на рис. 30). Ясно, что частица может находиться только в области X1 < X < X2 . Такое движение называется финитным. Далее, из соотношения 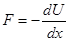 следует, что левее точки Х0 на частицу действует сила, направленная вправо, а правее точки Х0 – действует сила, направленная влево. В точке Х0 сама сила равна нулю (это положение равновесия). Такая сила называется возвращающей и, следовательно, частица совершает колебательное движение.
следует, что левее точки Х0 на частицу действует сила, направленная вправо, а правее точки Х0 – действует сила, направленная влево. В точке Х0 сама сила равна нулю (это положение равновесия). Такая сила называется возвращающей и, следовательно, частица совершает колебательное движение.
Рассмотрим теперь поведение частицы в другом поле консервативных сил (рис. 31).
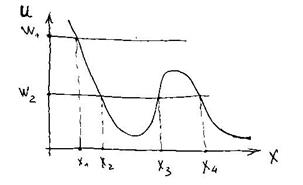 |
Рис. 31
Если задать значение механической энергии W2, то в области Х2 < X < X3 частица будет совершать колебательное движение. В область, правее координаты Х3 частица попасть вообще не сможет. Область типа Х1 – Х2 принято называть потенциальной ямой, а область типа Х3 – Х4 принято называть потенциальным барьером. Если же задать уровень механической энергии W1, то частица уйдет на бесконечность. Такое движение называют инфинитным.
9.Потенциальная энергия системы частиц:
а) собственная потенциальная энергия системы;
Перейдем теперь к системе частиц. Рассмотрим систему, состоящую из N частиц, между которыми действуют внутренние центральные силы. По определению, такие силы являются консервативными. Положение каждой частицы в системе определяется с помощью радиус-вектора, заданного относительно некоторого начала отсчета.
Покажем, что независимо от выбора начала отсчета работа всех внутренних сил пре переходе системы частиц из одного положения в другое может быть описана с помощью некоторой функции, зависящей только от относительного расположения части системы, т.е. от ее конфигурации.
Поскольку работа является величиной аддитивной, то элементарная работа, которую совершают все внутренние силы взаимодействия при перемещении частиц, может быть записана в следующем виде:
dA = dA1,2 + dA1,3 +…….+ dA1,N.
Причем, для каждой из этой пары консервативных сил выполняется следующее соотношение:
dAi,k = 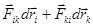 =
= 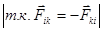 =
= 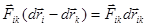 .
.
Здесь 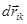 - перемещение частицы i относительно частицы k.
- перемещение частицы i относительно частицы k.
Можем ввести некоторую функцию Uik по следующему правилу: 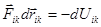 .
.
Эта функция, зависящая только от взаимного расположения частиц системы, называется собственной потенциальной энергией этих двух частиц. Тогда величину
Uсобств = U1,2 + U1,3 + ……..
Назовем собственной потенциальной энергией системы частиц.
Итак:
1) каждой конфигурации системы частиц соответствует свое значение собственной потенциальной энергии.
2) Работа всех внутренних консервативных сил при изменении конфигурации системы равна убыли собственной потенциальной энергии системы:
3)
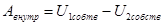 .
.
б) внешняя потенциальная энергия системы.
Рассмотрим теперь систему частиц, находящуюся во внешнем поле консервативных сил. Каждая частица системы в этом поле обладает некоторым значением потенциальной энергии Ui . Назовем внешней потенциальной энергией системы частиц сумму потенциальных энергий всех частиц, т.е. 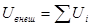 . Убыль внешней потенциальной энергии системы равна работе внешних сил:
. Убыль внешней потенциальной энергии системы равна работе внешних сил:
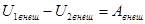 .
.
10.Кинетическая энергия системы частиц.
Назовем кинетической энергией системы частиц сумму кинетических энергий отдельных частиц системы 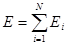 . Тогда приращение кинетической энергии системы равно работе всех сил, действующих на эту систему:
. Тогда приращение кинетической энергии системы равно работе всех сил, действующих на эту систему: 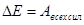 .
.
11. Связь между кинетическими энергиями системы частиц
в разных системах отсчета.
Рассмотрим систему N частиц, заданных с помощью радиус-векторов относительно некоторого начала отсчета 0. Тогда для кинетической энергии системы относительно этого начала можем записать:
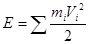 .
.
Свяжем с центром масс этой системы подвижную систему отсчета, которая перемещается относительно точки 0 со скоростью 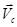 . По закону сложения скоростей Галилея:
. По закону сложения скоростей Галилея:
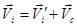 ,
,
здесь 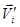 - скорость i-ой частицы относительно центра масс системы.
- скорость i-ой частицы относительно центра масс системы.
Тогда кинетическая энергия системы относительно точки 0 равна:
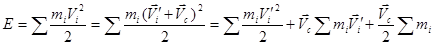 .
.
Второе слагаемое в правой части этого выражения равно нулю, т.к. в системе центра масс сам центр масс покоится, следовательно:
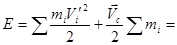
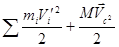 .
.
Здесь М – масса всей системы частиц.
Кинетическая энергия системы частиц складывается из кинетической энергии движения частиц относительно центра масс (относительного движения) и кинетической энергии всей системы, помещенной в центр масс, и движущейся со скоростью центра масс.
12. Механическая энергия системы.
Закон изменения и сохранения механической энергии системы.
Назовем механической энергией системы частиц сумму ее кинетической и потенциальной энергий. Если на систему действуют внешние и внутренние силы (потенциальные и не потенциальные), то механическая энергия системы изменяется по закону:
E + U = Aдисс .
Здесь Aдисс . есть суммарная работа всех диссипативных сил (внешних и внутренних). Если диссипативных сил нет, то выполняется закон сохранения механической энергии системы.
VI.Соударение тел
Законы сохранения энергии и импульса могут быть использованы для нахождения связей между физическими величинами, описывающими движение тел.
В физике под столкновением в общем случае понимают процессы взаимодействия между телами, а не простое соприкосновение тел. Проходя друг относительно друга, тела взаимодействуют между собой посредством силовых полей (например, гравитационных). В результате этого могут происходить различные процессы – тела могут соединиться вместе ( неупругое соударение), могут остаться после удара два тела (упругий удар), тела могут просто изменить траекторию своего движения. Примером последнего взаимодействия может служить рассеяние  - частиц на атомах вещества (опыт Резерфорда).
- частиц на атомах вещества (опыт Резерфорда).
1.Абсолютно неупругий удар
Внешним признаком абсолютно неупругого удара является наличие двух тел после удара и одного, объединенного, тела после удара. Поскольку мы рассматриваем замкнутую систему, то выполняется закон сохранения импульса. Закон сохранения механической энергии не выполняется, т.к. действую в системе диссипативные силы. При неупругом ударе часть механической энергии переходит в тепло.
Рассмотрим два шара массами m1 и m2, движущиеся со скоростями 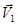 и
и 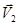 . Мы будем иметь дело с центральным ударом, при котором векторы скорости шаров до и после удара направлены по линии, соединяющей центры шаров. После удара образуется тело массой (m1 + m2), движущееся со скоростью
. Мы будем иметь дело с центральным ударом, при котором векторы скорости шаров до и после удара направлены по линии, соединяющей центры шаров. После удара образуется тело массой (m1 + m2), движущееся со скоростью 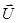 . Запишем закон сохранения импульса системы шаров:
. Запишем закон сохранения импульса системы шаров:
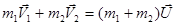 .
.
Отсюда находим скорость образовавшегося тела после удара:
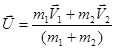 .
.
Рассчитаем потерю механической энергии (в данном случае только кинетической) в ходе этого процесса. Для этого найдем разность суммарной кинетической энергии тел до удара и кинетической энергии тела после удара:
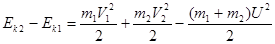 .
.
После подстановки в это выражение значение скорости тела после удара, получим:
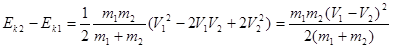 .
.
Видно, что по физическому смыслу это есть кинетическая энергия относительного движения шаров. Итак, при абсолютно неупругом ударе теряется кинетическая энергия относительного движения.
2.Абсолютно упругий удар
Рассмотрим замкнутую систему двух упругих шаров массами m1 и m2, движущихся со скоростями 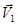 и
и 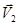 . После центрального удара обозначим скорости шаров
. После центрального удара обозначим скорости шаров 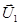 и
и 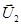 .
.
Запишем закон сохранения механической (кинетической) энергии и закон сохранения импульса:
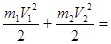
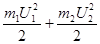
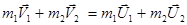
Для решения этой системы уравнений проделаем следующие преобразования:
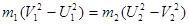
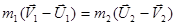
Разделим почленно правые и левые части этой системы:
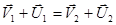 .
.
Выразим отсюда скорость второго шара после удара:
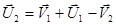
Подставим это в закон сохранения импульса и после преобразований получим:
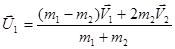 .
.
Аналогично можно получить:
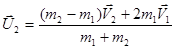
При равенстве масс сталкивающихся шаров имеем: 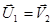 и
и 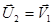 , т.е. шары обмениваются скоростями.
, т.е. шары обмениваются скоростями.
Дата добавления: 2018-11-26; просмотров: 1152;











