Момент импульса частицы и системы частиц
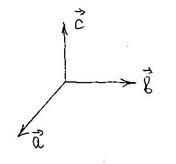 Кроме сохранения импульса и энергии в замкнутых системах сохраняется еще одна физическая величина – момент импульса. Рассмотрим сначала векторное произведение векторов
Кроме сохранения импульса и энергии в замкнутых системах сохраняется еще одна физическая величина – момент импульса. Рассмотрим сначала векторное произведение векторов 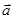 и
и 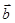 (рис. 32).
(рис. 32).
Рис. 32
Векторным произведение векторов 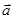 и
и 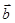 называется такой вектор
называется такой вектор 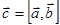 , модуль которого равен:
, модуль которого равен:
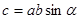 ,
,
где 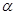 - угол между векторами
- угол между векторами 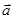 и
и 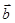 .
.
Направление вектора 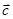 определяется по правилу буравчика, если его вращать от
определяется по правилу буравчика, если его вращать от 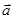 к
к 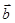 по кратчайшему пути.
по кратчайшему пути.
Существует выражение для определения векторного произведения:
С = 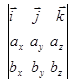 .
.
1. Момент силы относительно точки и относительно оси.
Введем сначала понятие момента силы. Пусть на частицу, положение которой определяется с помощью радиус-вектора 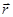 относительно начала отсчета точки 0, действует некоторая сила
относительно начала отсчета точки 0, действует некоторая сила 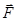 (рис. 33).
(рис. 33).
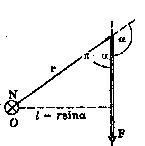
Рис. 33
Назовем моментом силы 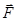 относительно точки 0 векторную величину:
относительно точки 0 векторную величину:
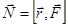 .
.
В данном случае вектор момента силы направлен перпендикулярно плоскости рисунка к нам. Из рисунка следует, что величина 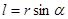 . Назовем ее плечом момента силы. Плечом момента силы называется расстояние от точки отсчета 0 до линии действия силы.
. Назовем ее плечом момента силы. Плечом момента силы называется расстояние от точки отсчета 0 до линии действия силы.
Моментом силы относительно некоторой оси, проходящей через точку 0, называется проекция вектора момента силы относительно точки 0 на эту ось.
2.Момент пары сил. Свойства момента пары сил.
Рассмотрим две параллельные, равные по модулю, противоположные по направлению силы, не действующие вдоль одной прямой (рис.34). Такие силы называют парой сил. Расстояние 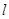 между прямыми, вдоль которых действуют эти силы, называется плечом пары.
между прямыми, вдоль которых действуют эти силы, называется плечом пары.
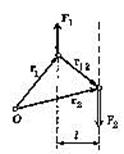 |
Рис. 34
Здесь введены следующие обозначения:
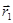 - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы 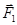 ,
,
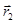 - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы 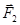 ,
,
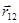 - радиус-вектор точки приложения силы
- радиус-вектор точки приложения силы 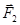 относительно точки приложения силы
относительно точки приложения силы 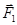 .
.
Суммарный момент этой пары сил определим как:
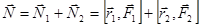 .
.
Поскольку силы образуют пару, то 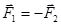 , следовательно:
, следовательно:
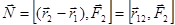 .
.
Видно, что момент пары сил не зависит от выбора начала отсчета точек приложения сил.
3.Момент импульса частицы относительно оси и относительно точки.
 Обратимся теперь к понятию момента импульса. Пусть частица массой m, положение которой определяется с помощью радиус-вектора
Обратимся теперь к понятию момента импульса. Пусть частица массой m, положение которой определяется с помощью радиус-вектора 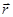 относительно начала отсчета точки 0, движется со скоростью
относительно начала отсчета точки 0, движется со скоростью 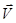 (рис. 35).
(рис. 35).
Рис. 35
Введем вектор 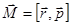 , который назовем моментом импульса частицы относительно точки 0. Величину
, который назовем моментом импульса частицы относительно точки 0. Величину 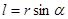 назовем плечом момента импульса относительно точки 0.
назовем плечом момента импульса относительно точки 0.
Моментом импульса относительно оси, проходящей через точку 0, назовем проекцию момента импульса относительно точки на эту ось.
Примеры.
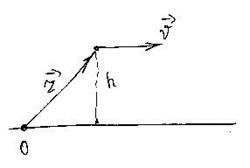 1. Рассмотрим движение вдоль прямой линии. На высоте h летит горизонтально самолет массой m со скоростью V (рис.36).
1. Рассмотрим движение вдоль прямой линии. На высоте h летит горизонтально самолет массой m со скоростью V (рис.36).
Рис. 36
Найдем момент импульса самолета относительно некоторой точки 0. Модуль момента импульса равен произведению импульса на его плечо. В данном случае плечо импульса равно h. Следовательно:
M= 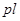 = mVh =const.
= mVh =const.
2. Рассмотрим движение по окружности. Частица массой m движется по окружности радиуса R с постоянной по модулю скоростью V (рис.37). Найти момент импульса частицы относительно центра окружности 0.
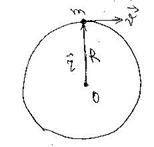 |
Рис. 37
Момент импульса частицы M= 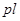 = рR=const.
= рR=const.
4.Уравнение моментов частицы
.
По определению момент импульса частицы относительно некоторой точки 0 равен:
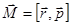 .
.
Найдем производную по времени правой и левой части этого выражения:
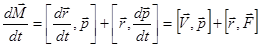 .
.
Первое слагаемое по правилу векторного произведения обращается в нуль. Имеем окончательно:
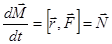 .
.
Это выражение называют уравнением моментов частицы.
Скорость изменения момента импульса равна моменту сил.
5.Момент импульса системы частиц.
Закон изменения и сохранения момента импульса системы частиц.
Рассмотрим систему взаимодействующих между собой частиц, на которую действуют внешние силы. Зададим положение в пространстве частиц этой системы с помощью радиус-векторов относительно некоторого начала отсчета 0. Запишем суммарный момент импульса этой системы относительно точки:
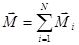 .
.
Найдем изменение суммарного момента:
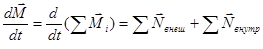 .
.
Запишем эту систему уравнений:
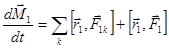 .
.
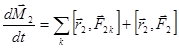 .
.
…………………………………..
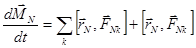 .
.
Просуммируем левые и правые части этой системы и рассмотрим по парные суммы в первом слагаемом справа.
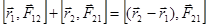 = 0.
= 0.
По третьему закону Ньютона в нуль обратятся и все остальные по парные суммы. Следовательно, суммарный момент всех внутренних сил взаимодействия между частицами равен нулю. Тогда остается:
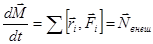 .
.
Момент импульса системы частиц изменяет момент внешних сил. Для замкнутой системы частиц выполняется закон сохранения момента импульса.
6.Орбитальный и собственный моменты импульса системы частиц.
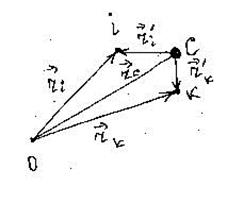 Рассмотрим систему N частиц, положение которых задается с помощью радиус-векторов относительно некоторого начала отсчета 0(рис.38).
Рассмотрим систему N частиц, положение которых задается с помощью радиус-векторов относительно некоторого начала отсчета 0(рис.38).
Рис. 38
Пусть положение центра масс С этой системы определяется с помощью радиус-вектора 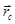 . Тогда положение i-ой частицы относительно начала 0 определится как:
. Тогда положение i-ой частицы относительно начала 0 определится как:
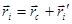 .
.
Запишем суммарный момент импульса системы частиц относительно начала 0:
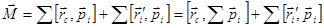 .
.
Первое слагаемое назовем орбитальным моментом импульса системы:
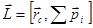 .
.
Второе слагаемое назовем собственным моментом импульса системы:
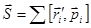 .
.
Тогда полный момент импульса системы относительно точки отсчета 0 имеет вид:
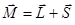 .
.
7.Движение в центральном поле сил.
Рассмотрим частицу, движущуюся в центральном силовом поле. Напомним, что в таком поле сила, действующая на частицу, зависит лишь от расстояния между частицей и началом отсчета. Кроме того, сила все время направлена вдоль радиус-вектора частицы.
Легко сообразить, что в таком случае момент центральной силы равен нулю и, следовательно, выполняется закон сохранения момента импульса относительно начала отсчета.
Поскольку 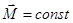 , то траектория частицы все время расположена в плоскости, в которой лежат векторы силы и радиус-вектор. В центральном поле частицы движутся по плоским траекториям.
, то траектория частицы все время расположена в плоскости, в которой лежат векторы силы и радиус-вектор. В центральном поле частицы движутся по плоским траекториям.
За время dt радиус-вектор частицы опишет площадь dS (рис.39).

Рис. 39
Эта площадь равна половине площади параллелограмма, построенного на радиус-векторе 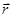 и векторе элементарного перемещения
и векторе элементарного перемещения 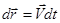 . Как известно, площадь такого параллелограмма равна модулю векторного произведения
. Как известно, площадь такого параллелограмма равна модулю векторного произведения 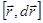 . Таким образом, можем теперь записать:
. Таким образом, можем теперь записать:
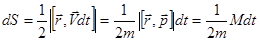 .
.
Назовем величину 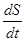 - секториальной скоростью, и для нее получим выражение:
- секториальной скоростью, и для нее получим выражение:
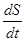 =
= 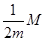 .
.
Т.к. в центральном поле М =const, то, следовательно, секториальная скорость остается постоянной величиной.
Вывод: при движении частицы в центральном силовом поле ее радиус-вектор за равные промежутки времени описывает равные площади.
Это утверждение и является вторым законом Кеплера.
8.Задача двух тел.
Задача о движении частицы в центральном силовом поле имеет много приложений. Рассмотрим задачу о движении двух тел. Рассмотрим две взаимодействующие только между собой частицы. Выясним, как ведет себя центр масс такой системы. Из теоремы о движении центра масс замкнутой системы можно сделать вывод, что он либо покоится, либо движется прямолинейно и равномерно.
Будем решать задачу двух тел в системе их центра масс. Как известно, радиус-вектор центра масс системы определяется с помощью выражения:
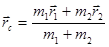 .
.
Из закона сохранения импульса такой замкнутой системы следует, что:
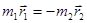
Введем радиус-вектор, определяющий положение второй частицы относительно первой (рис. 40):
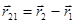

Рис. 40
Тогда можно получить выражения для связи радиус-векторов, определяющих положение частиц относительно их общего центра масс, с радиус-вектором их относительного положения:
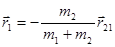 ,
, 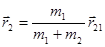 .
.
Рассмотрим теперь эту задачу с энергетической точки зрения. Обозначим через 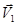 и
и 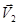 -скорости частиц относительно их центра масс, а через
-скорости частиц относительно их центра масс, а через 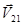 - скорость второй частицы относительно первой. Тогда из закона сохранения импульса системы частиц можно получить следующие выражения:
- скорость второй частицы относительно первой. Тогда из закона сохранения импульса системы частиц можно получить следующие выражения:
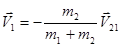 ,
, 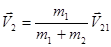 .
.
Запишем полную механическую энергию этой системы частиц:
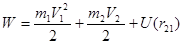 .
.
Здесь U(r21) – собственная потенциальная энергия системы.
Это выражение можно преобразовать следующим образом:
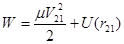 ,
,
где введено следующее обозначение 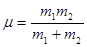 - приведенная масса.
- приведенная масса.
Мы видим с точки зрения энергии, эта система частиц ведет себя, как одна частица с приведенной массой и движущейся с относительной скоростью. Задача двух тел сводится к задаче о движении одного тела.
Если известна зависимость 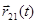 , то можно решить и основную задачу, т.е. найти зависимости
, то можно решить и основную задачу, т.е. найти зависимости 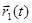 и
и 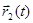 .
.
Запишем уравнение движения (второй закон Ньютона) для каждой из частиц в центральном поле:
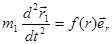
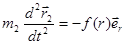
В правой части второго уравнения стоит знак минус, т.к 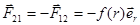 .
.
Разделив первое уравнение на m1, а второй – на m2, получим:
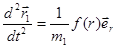
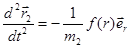
Вычтем первое уравнение из второго:
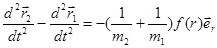 .
.
Тогда окончательно:
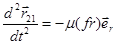 .
.
Отсюда можно найти зависимость 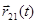 .
.
9.Движение искусственных спутников. Космические скорости.
Рассмотрим движение искусственного спутника Земли вблизи ее поверхности. Поскольку на спутник действует только одна сила – сила гравитационного притяжения к Земле, то можно записать уравнение его движения по окружности:
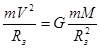 ,
,
где m –масса спутника, М – масса Земли, Rз –радиус Земли.
Отсюда можно получить скорость спутника:
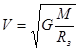 .
.
Подставив соответствующие значения, получим скорость V1 = 8 км/с.
Эта скорость называется первой космической (скорость, которую необходимо сообщить телу, чтобы оно стало спутником Земли вблизи ее поверхности).
Мы рассмотрели простейший случай движения спутника по круговой орбите. Однако, как показывает теория, в задаче двух тел возможны и другие траектории движения одной частицы относительно другой – эллипсы, гиперболы и параболы. Эллиптическим орбитам соответствует отрицательное значение полной механической энергии системы, гиперболическим орбитам соответствует положительное значение полной механической энергии и параболическим орбитам соответствует значение полной механической энергии, равное нулю.
Найдем, так называемую, вторую космическую скорость. Это скорость, которую надо сообщить телу, чтобы оно стало спутником Солнца, при этом тело должно двигаться по параболической траектории.
Запишем полную механическую энергию системы спутник – Земля, считая Землю неподвижной:
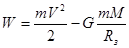 .
.
Приравняв полную механическую энергию нулю, получим вторую космическую скорость:
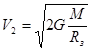 .
.
Подставив соответствующие значения, получим V2 = 11,2 км/с.
МЕХАНИКА ТВЕРДОГО ТЕЛА
VIII. Кинематика твердого тела
1.Абсолютно твердое тело. Плоское движение твердого тела и его разложение на поступательное и вращательное..
До сих пор в качестве физической модели мы использовали материальную точку, однако не все задачи могут быть решены в этом приближении. Перейдем теперь к рассмотрению так называемых абсолютно твердых тел. Абсолютно твердым телом называется такое тело, в котором не меняется расстояние между частицами, из которых оно состоит. Иными словами, это абсолютно не деформируемое тело.
Будем рассматривать плоское движение твердого тела, при котором во время движения любая его точка остается в одной из параллельных плоскостей. При плоском движении траектории каждой точки твердого тела лежит в одной плоскости, причем плоскости всех траекторий либо совпадают, либо параллельны.
Любое сложное движение твердого тела можно представить в виде суммы более простых движений: поступательного и вращательного. Поступательным называется такое движение твердого тела, при котором линия, соединяющая две любые точки тела, сохраняет направление в пространстве. Поступательное движение не обязательно является прямолинейным, например, кабина в чертовом колесе (рис.41).

 Рис. 41
Рис. 41
Вращательным называется такое движение, при котором траектории всех точек твердого тела являются концентрическими окружностями с центром, лежащим на оси вращения. Катящийся по столу цилиндр совершает и поступательное движение и вращательное движение вокруг своей оси симметрии.
Покажем, как плоское движение может быть разложено на поступательное и вращательное (рис. 42).

Рис. 42
Из рисунка видно, что из положения 1 в положение 2 тело можно перемещать сначала в положение 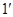 поступательно, а затем в положение 2 вращательно вокруг оси
поступательно, а затем в положение 2 вращательно вокруг оси 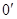 . Такое разбиение на поступательное и вращательное движение можно производить бесконечно большим числом способов, но при этом поворот осуществляется всегда на один и тот же угол
. Такое разбиение на поступательное и вращательное движение можно производить бесконечно большим числом способов, но при этом поворот осуществляется всегда на один и тот же угол 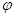 .
.
Таким образом, плоское движение может представлено как поступательное с одинаковой для всех точек тела скоростью 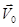 и вращательное с одинаковой угловой скоростью
и вращательное с одинаковой угловой скоростью 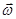 . Для линейных скоростей точек твердого тела это может быть записано в виде:
. Для линейных скоростей точек твердого тела это может быть записано в виде:
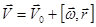 .
.
Здесь 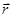 - радиус-вектор любой точки твердого тела.
- радиус-вектор любой точки твердого тела.
Например, качение цилиндра по горизонтальной поверхности (рис.43) можно представить как поступательное движение всех точек со скоростью V0 и вращение вокруг оси, совпадающей с его осью симметрии 0, с угловой скоростью 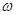 ., либо как поступательное движение со скоростью
., либо как поступательное движение со скоростью 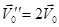 и вращение с той же угловой скоростью
и вращение с той же угловой скоростью 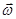 , но вокруг оси
, но вокруг оси 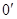 .
.

Рис. 43
Перемещение твердого тела можно представить как совокупность одних лишь поворотов вокруг, так называемой, мгновенной оси. Эта ось может находиться либо в пределах самого твердого тела, но может быть и за его пределами. Положение мгновенной оси со временем меняется. В случае качения цилиндра мгновенная ось совпадает с линией касания цилиндра с плоскостью.
Изобразим на рис. 44 направление мгновенных скоростей некоторых точек цилиндра относительно неподвижной системы отсчета. Скорость точки А равна в каждый момент времени нулю, т.к. она складывается из поступательной скорости 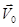 и равной по модулю линейной скоростью
и равной по модулю линейной скоростью 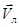 . Скорость точки С равна удвоенной скорости
. Скорость точки С равна удвоенной скорости 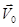 и т.д.
и т.д.

Рис. 44
Посмотрим, как ориентирована скорость относительно неподвижной системы отсчета любой точки цилиндра. Для этого запишем условие абсолютно твердого тела для двух произвольных точек в следующем виде:
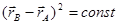 .
.
Продифференцируем по времени правую и левую часть:
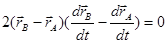 .
.
Свяжем точку А с мгновенной осью вращения, тогда 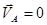 и
и 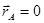 . Следовательно, имеем:
. Следовательно, имеем:
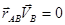 .
.
Из этого условия следует перпендикулярность соответствующих векторов, т.е. 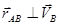 .
.
Дата добавления: 2018-11-26; просмотров: 1140;











