Ранг матриц. Теорема о базисном миноре

Сначала введем понятие линейной зависимости и независимость строк (столбцов) матрицы.

Определение 6.Строки 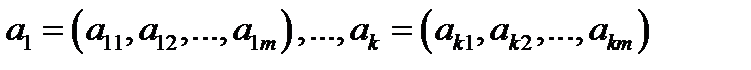называются линейно зависимыми, если существуют числа 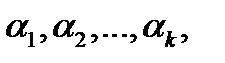не равные нулю одновременно, такие, что имеет место равенство

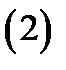
Если же равенство (2) (где 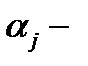числа) имеет место тогда и только тогда, когда все числа 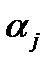одновременно равны нулю ( 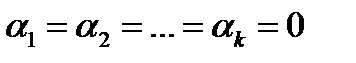), то строки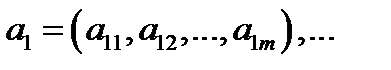 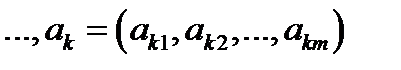называются линейно независимыми. Аналогичные понятия вводятся и для столбцов.

Например, строки 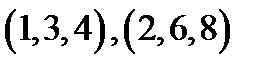линейно зависимы, так как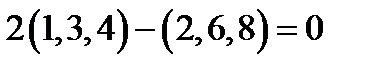

(здесь 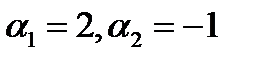), а столбцы 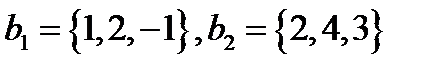линейно независимы, так как

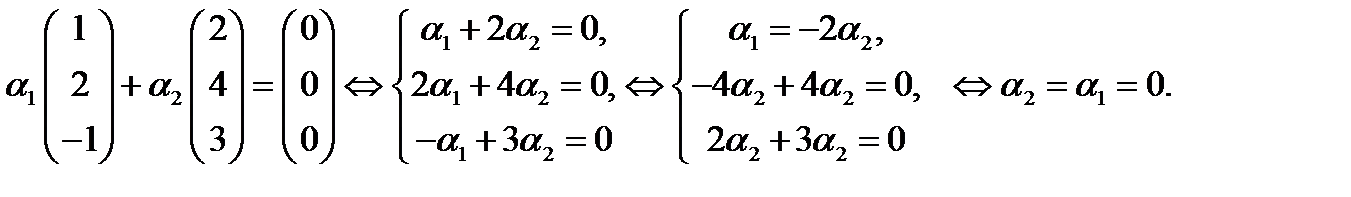
Введем теперь следующее важное понятие.

Определение 7.Рангом произвольной матрицы 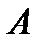(размера 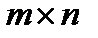) называется максимальное число линейно независимых столбцов этой матрицы. Обозначение: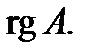

Например, ранг матрицы 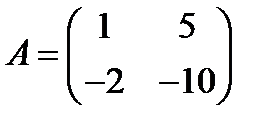равен 1, так как только один столбец этой матрицы (любой) линейно независим, а два столбца линейно зависимы.

Пусть дана произвольная матрица 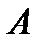. Будем последовательно рассматривать в ней миноры первого, второго, третьего и т.д. порядков.

Определение 8.Базисным минором матрицы 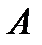называется такой отличный от нуля минор 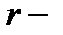го порядка, что все миноры матрицы 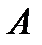порядка выше 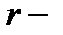го равны нулю.

Нетрудно доказать следующее утверждение.

Теорема о базисном миноре.Ранг матрицы 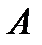равен порядку базисного минора этой матрицы.

Отсюда, в частности, следует, что при транспонировании матрицы ее ранг не изменяется, поэтому ранг матрицы равен также максимальному числу ее линейно независимых строк. Из теоремы о базисном миноре также вытекает, что ранг матрицы ступенчатого вида равен числу её опорных элементов.

Лекция 4. Элементарные преобразования и приведение матрицы к ступенчатому виду. Линейные системы алгебраических уравнений. Линейное пространство, размерность, базис. Теорема Кронекера-Капелли. Структура общего решения однородной и неоднородной систем уравнений. Метод Гаусса решения алгебраических систем уравнений

В основе решения систем линейных уравнений лежат два метода – метод Крамера и метод Гаусса, к изложению которых мы переходим.