Определители матрицы и их свойства

Мы имели уже дело с определителями второго и третьего порядков на предыдущих лекциях. Дадим теперь общее понятие определителя 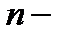порядка по индукции. Любой квадратной матрице вида

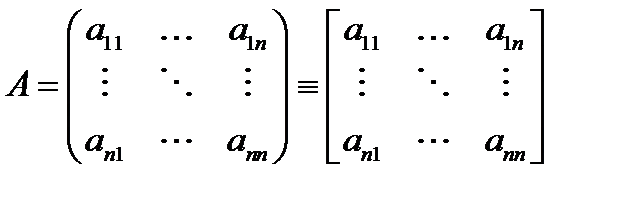
ставится в соответствие число

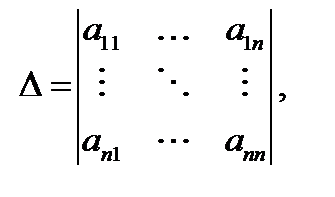
определяемое ниже (см. определение 5) и называемое определителем (или детерминантом) матрицы 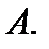Теперь введем понятие минора матрицы.

Определение 3.В матрице 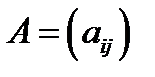на пересечении любых 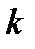строк и 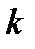столбцов стоит матрица 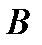порядка 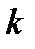. Определитель матрицы 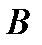называется минором 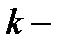го порядка матрицы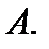

Ясно, таких миноров может быть несколько. Пусть теперь матрица 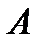является квадратной.

Определение 4.Минор 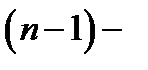порядка, полученный из матрицы 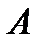после вычеркивания её 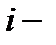строки и 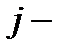го столбца, называется дополнительным минором элемента 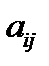этой матрицы (обозначение: 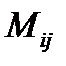). Число 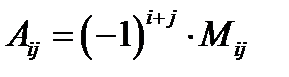называется алгебраическим дополнением элемента 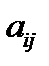матрицы .

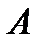Определение 5. Пустьв квадратной матрице 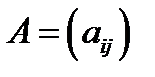выделена произвольная строка 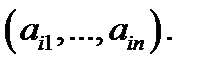Определителем матрицы 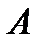называется число

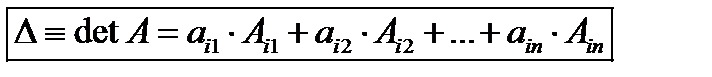
(т.е. сумма произведений элементов 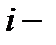й строки на их алгебраические дополнения). Часто определитель матрицы обозначают так: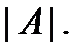

Как мы уже отметили выше, определитель порядка 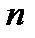вычисляется по индукции: если известно правило вычисления определителей 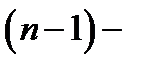порядка, то определитель 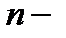порядка вычисляется по формуле (1). Ранее было даны правила вычисления определителей второго и третьего порядков, поэтому по формуле (1) можно вычислить определители четвертого порядка и выше. Например,

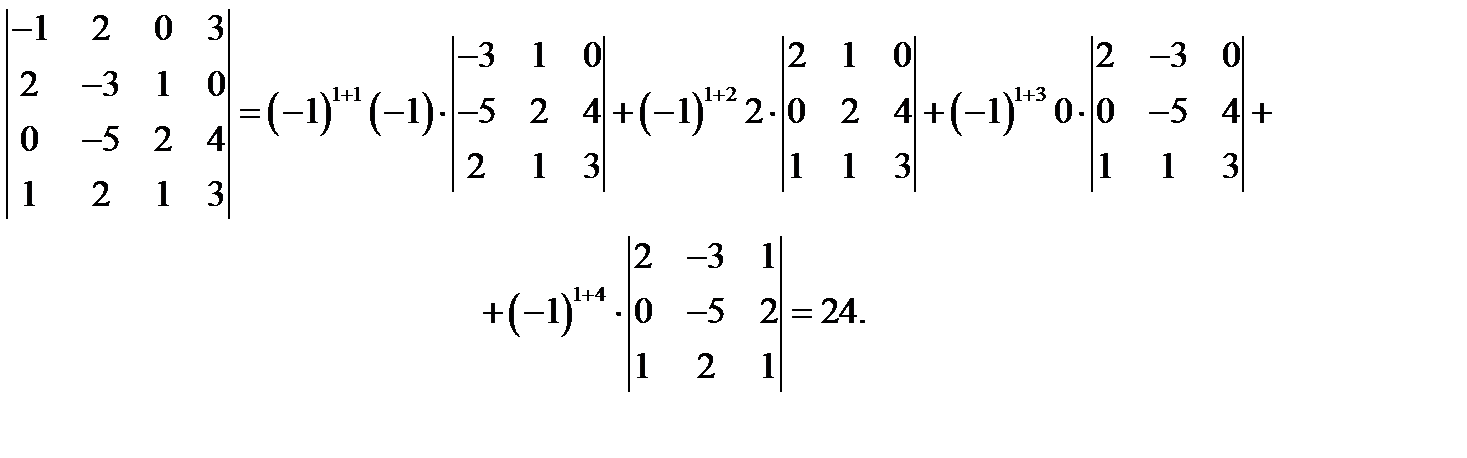
Перечислим основные свойства определителей. Сначала заметим, что матрица 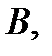полученная из матрицы 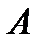заменой строк на столбцы с теми же номерами, называется тран-

спонированной к 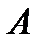матрицей. Обозначение: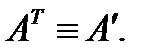

1) При транспонировании матрицы 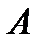ее определитель не изменяется: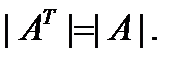

2) При перестановки каких-либо двух строк (или двух столбцов) матрицы ее определитель изменяет знак на противоположный.

3) Определитель, у которого есть нулевая строка (или нулевой столбец) равен нулю.

4) Определитель, у которого элементы одной строки (или столбца) пропорциональны элементам другой строки (или столбца ) равен нулю.

5) Общий множитель элементов любой строки (или столбца) можно выносить за знак определителя :

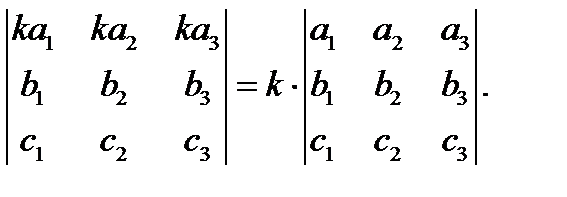
6) Если к какой-нибудь строке определителя прибавить другую строку, умноженную на любое число 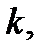то определитель не изменится. Тоже верно и для столбцов определителя.

7) (сумма определителей)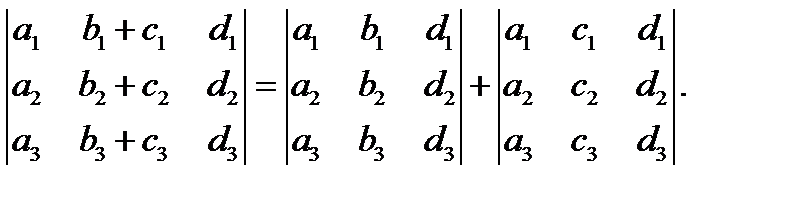

8) Определитель произведения двух квадратных матриц одной и той же размерности равен произведению определителей этих матриц: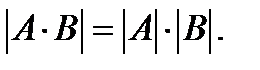

Доказательствовсех этих свойств проводится с использованием определения 5. Докажем, например, свойство 5. Имеем

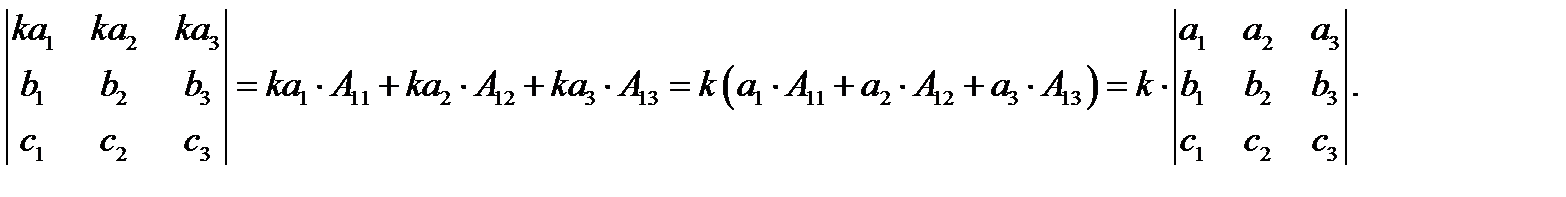
Свойство 5 доказано.