Линейные системы уравнений с квадратной матрицей. Правило Крамера

Итак, рассмотрим систему 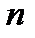линейных уравнений

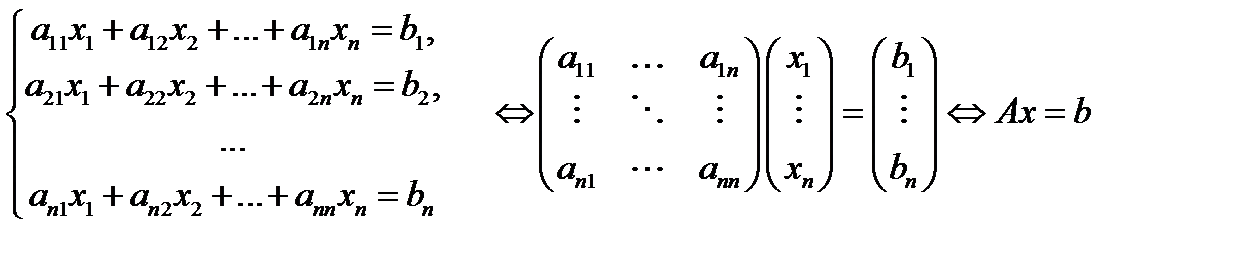
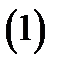
с 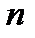неизвестными 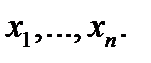Матрица 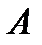этой системы квадратная, поэтому можно вычислить ее определитель (называемый главным определителем системы (1)). Ниже будут участвовать и другие определители, относящиеся к системе (1). Введем их. Если в определителе выбросить 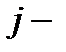й столбец и заменить его на столбец 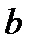свободных членов, то получим определитель

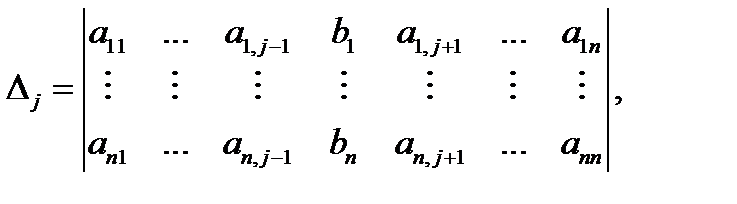
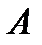называемый м вспомогательным определителем Если определитель то для матрицы существует обратная матрица 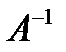и эта матрица единственна. С помощью неё можно решить систему (1). Действительно, умножая обе части последнего равенства (1) на 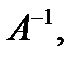будем иметь 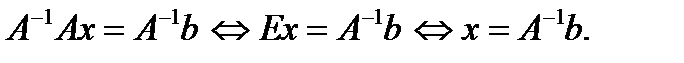Мы доказали следующее утверждение.

Теорема 1.Если 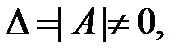то система (1) имеет единственное решение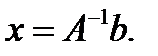

Пример 1.Решить систему уравнений

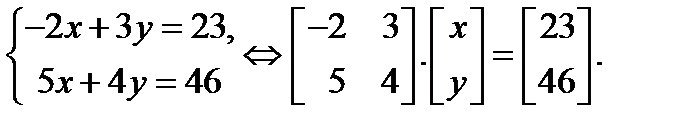
Решение. Так как определитель 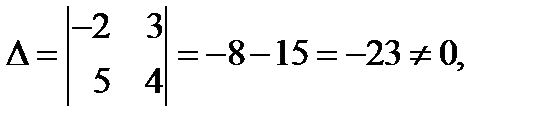то данная система имеет единственное решение

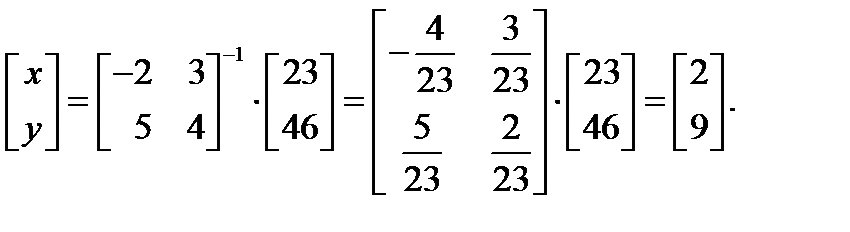
Другой способ решения системы (1) основан на следующем утверждении.

Теорема Крамера.Пусть в системе (1) хотя бы один из ее коэффициентов 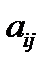не равен нулю. Тогда для того чтобы система (1) имела единственное решение, необходимо и достаточно, чтобы её главный определитель был не равен нулю. В этом случае решение системы (1) даётся формулами Крамера:

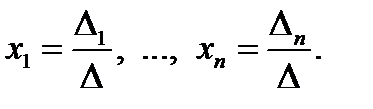
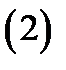
Если 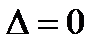и хотя бы один из определителей 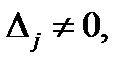то система (1) решений не имеет. Если все 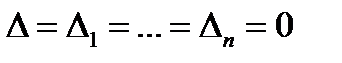, то система (1) либо не имеет решений вообще, либо имеет их бесчисленное множество.

Доказательствопроведем в случае 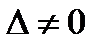для системы

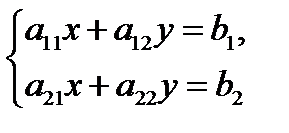
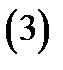
с двумя неизвестными Не умаляя общности, можно считать, что 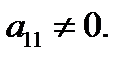Из первого уравнения (3) находим 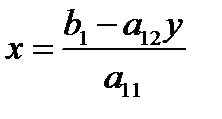и подставляем во второе уравнение; будем иметь

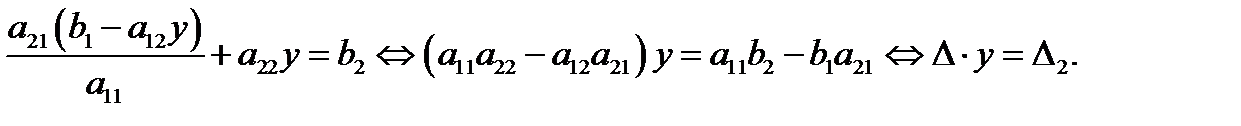
Пусть теперь 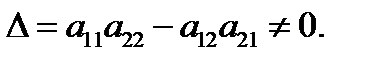тогда 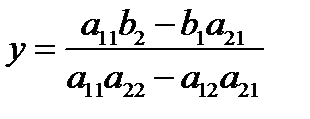, поэтому

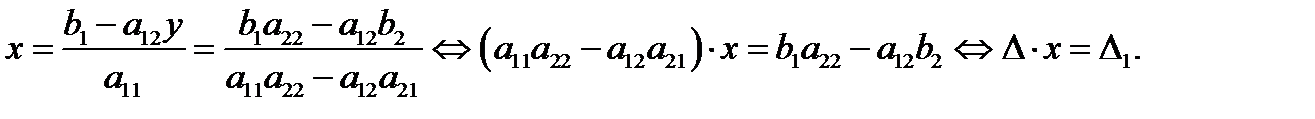
Мы показали, что в случае 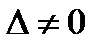исходная система (3) равносильна системе двух уравнений 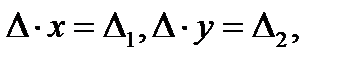поэтому если 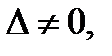то система (3) имеет единственное решение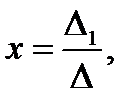 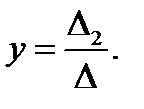Теорема доказана.

Геометрическая интерпретация теоремы Крамера. Уравнения (3) есть уравнения прямых на плоскости Если 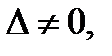то коэффициенты указанных прямых не пропорциональны, значит, эти прямые не параллельны (см. Р.7), и поэтому пересекаются в одной точке (в точке 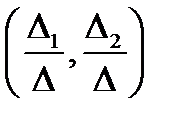). Если 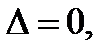то коэффициенты прямых (3) пропорциональны, т.е. 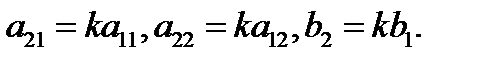В этом случае система (3) равносильна одному уравнению 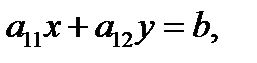которое имеет бесчисленное множество решений 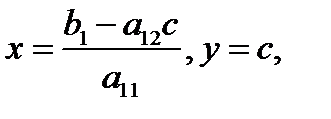где 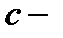произвольная постоянная, т.е. все точки прямой 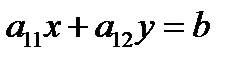(см. Р.8) являются решениями системы (3). И, наконец, если 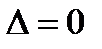и хотя бы один из определителей 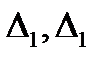не равен нулю, то прямые (3) паралельны, а, значит, система (3) не имеет решений (см. Р.9).

Пример 2.Решить систему уравнений

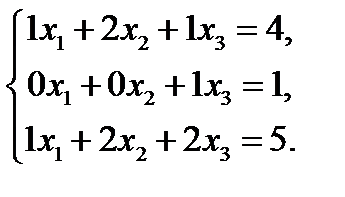
Решение.Вычисляем определители

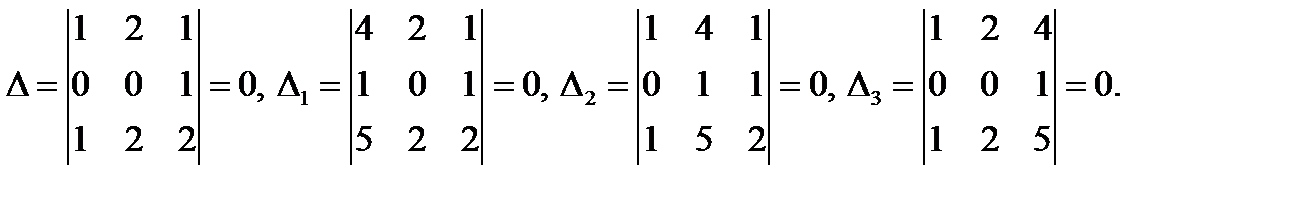
По теореме Крамера эта система либо имеет бесчисленное множество решений, либо не имеет их вообще. В нашем случае 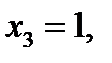поэтому первое и третье уравнения принимают вид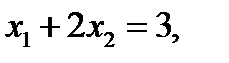 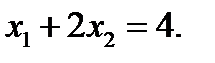Ни при каких 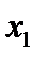и 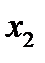эти равенства одновременно не выполняются, значит данная система решений не имеет.