Матрицы и действия над ними. Матрицы специального вида

Определение 1.Матрицей размера 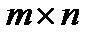называют таблицу чисел

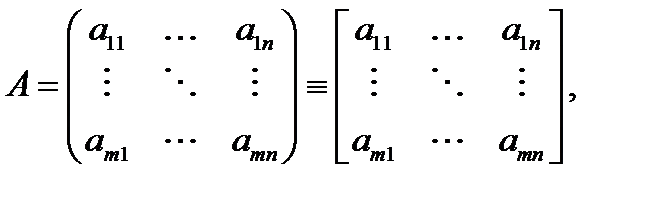
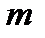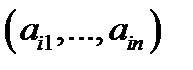состоящую из строк и 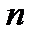столбцов 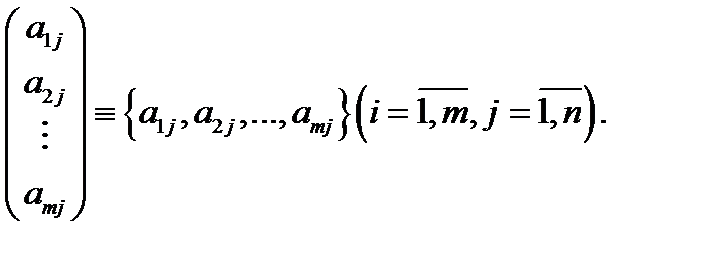При этом числа[1] 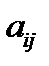называются элементами матрицы 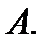Матрицу 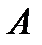называют квадратной матрицей размерности 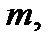если число 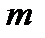ее строк совпадает с числом столбцов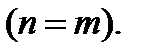

Часто матрицу обозначают так: 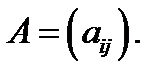Желая указать размеры матрицы, будем писать 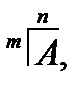а саму матрицу будем называть 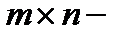матрицей.

Действия сложения и вычитания над матрицами одинакового размера определяются равенствами:

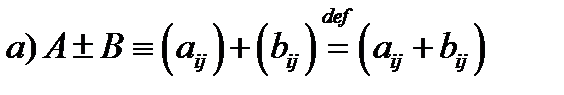
(т.е. при сложении или вычитании матриц складываются (соответственно вычитаются) их элементы, находящиеся на одинаковых местах).

Умножение матрицы на число определяется равенством

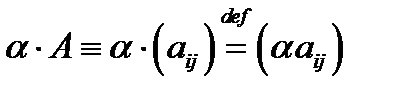
(т.е. при умножении матрицы на число надо каждый элемент этой умножить на это число).

Матрицы можно умножать друг на друга только в том случае, когда их размеры согласованы, т.е., когда число столбцов первой матрицы равно числу строк второй матрицы:

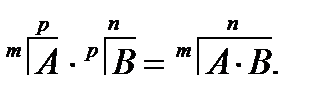Сначала определяют произведение вектор-строки 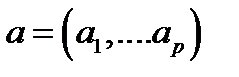на

вектор-столбец 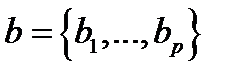(имеющих одинаковое число компонент):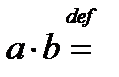

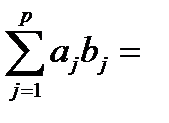
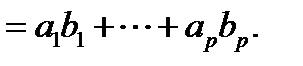Затем определяют

в) произведением матриц 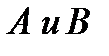с согласованными размерам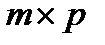и и 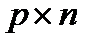называется 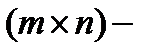матрица 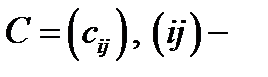й элемент которой получен умножением 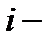й строки матрицы 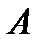на 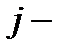й столбец матрицы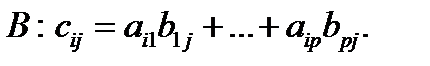

Например,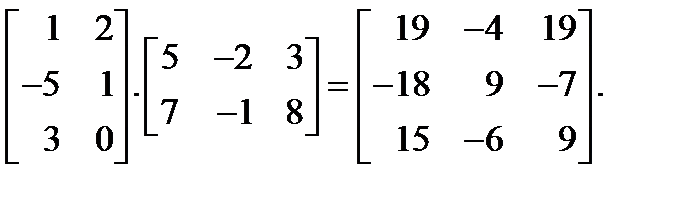

Часто встречаются матрицы следующего специального вида:

1. Единичная матрица: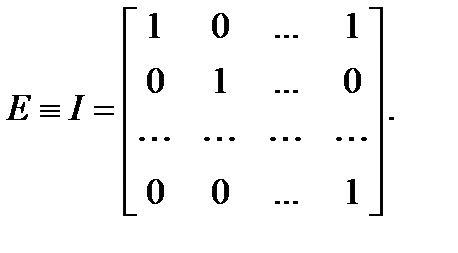

2. Диагональная матрица: 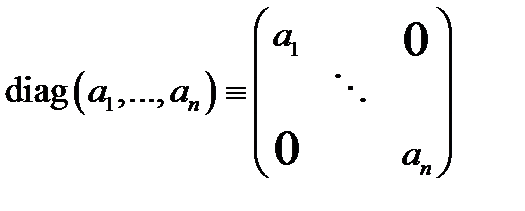(здесь и в матрице 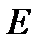все элементы вне главной диагонали 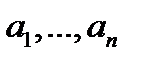равны нулю).

3.Треугольная матрица: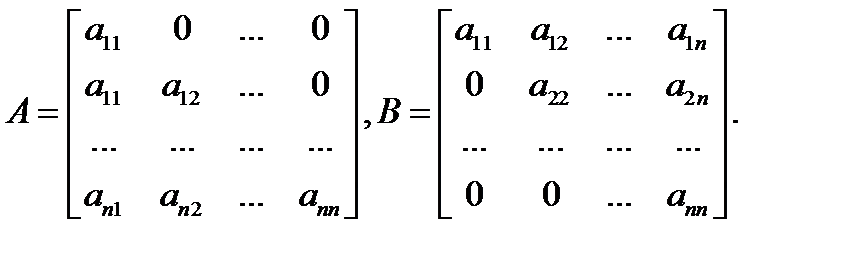

4. Матрица трапециевидной формы: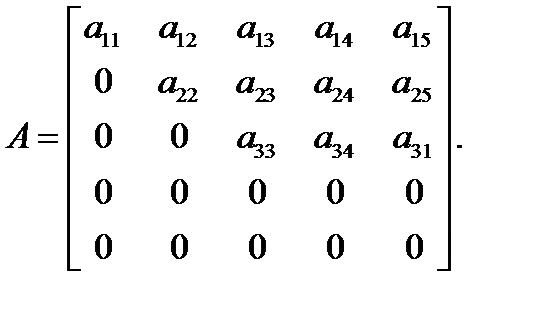

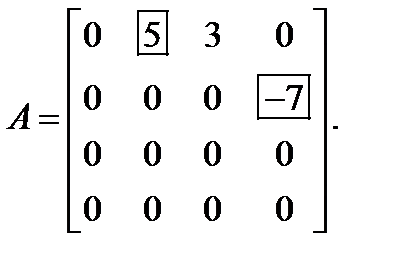
При решении линейных систем уравнений будут встречаться матрицы ступенчатого вида. Чтобы описать их, введем понятие опорного элемента строки. Это не равный нулю первый слева элемент строки. Например, в строке 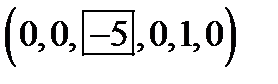элемент (-5) является опорным (здесь и ниже в рамке указан опорный элемент).

Определение 2.Матрица 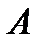называется матрицей ступенчатого вида, если в ней:

а) опорный элемент каждой строки находится правее опорного элемента предыдущей строки;

б) если в матрице есть нулевая строка, то и все следующие ее строки также нулевые.

Ясно, что диагональная, верхне-треугольная и трапециевидная матрицы являются ступенчатыми. Другой пример матрицы ступенчатого вида: