Отношения следования и равносильности между предложениями
Рассмотрим две высказывательные формы: «число х кратно 4» и «число х кратно 2», заданные на множестве N натуральных чисел.
Как связаны между собой эти два предложения?
Можно сказать так: из того, что число х кратно 4, следует, что х кратно 2. Это мы можем утверждать, потому что знаем - при всех значениях х, при которых истинно предложение
«число х кратно 4», будет истинно и предложение «число х кратно 2». В этом случае говорят, что данные предложения находятся в отношении логического следования.
Определение. Высказывательная форма В(х) следует из высказывательной формы А(х), если В(х) обращается в истинное высказывание при всех тех значениях х, при которых А (х) истинна.
Пусть А и В - высказывания, тогда говорят, что из А следует В, если всякий раз, когда А истинно, истинно и В.
Для обозначения отношения логического следования используется знак =>. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) => В(х), прочитать которое можно по разному:
1) Из А(х) следует В(х).
2) Всякое А(х) есть В(х).
3) Если А(х), то В(х).
4) В(х) есть следствие А(х).
5) А(х) есть достаточное условие для В(х).
6) В(х) есть необходимое условие для А(х).
Например, утверждение о том, что из предложения «число х кратно 4», следует предложение «число х кратно 2», можно сформулировать еще так:
- Всякое число, которое кратно 4, кратно и 2.
- Если число кратно 4, то оно кратно и 2.
- Кратность числа 2 есть следствие кратности его 4.
- Кратность числа 4 есть достаточное условие для его кратности 2.
- Кратность числа 2 есть необходимое условие для его кратности 4.
Последние два предложения часто формулируют в следующей форме:
- Для того чтобы число было кратно 2, достаточно, чтобы оно было кратно 4.
-Для того чтобы число было кратно 4, необходимо, чтобы оно было кратно 2.
Так как одно и то же утверждение «из А(х) следует В(х)» можно прочитать по-разному, надо уметь переходить от одной его формулировки к другой, не меняя смысла.
Задача 1. Данные предложения переформулируйте, используя различные способы прочтения утверждений А(х) => В(х):
а) Всякий квадрат является прямоугольником.
б) Для того чтобы число делилось на 5, достаточно, чтобы его запись оканчивалась нулем.
Решение, а) В данном высказывании можно выделить два предложения: А(х)- «четырехугольник- квадрат» и В(х) - «четырехугольник - прямоугольник». Они находятся в отношении следования: А(х) => В(х), которое выражено предложением со словом «всякий». Данное высказывание можно переформулировать:
1) Из того, что четырехугольник- квадрат, следует, что он прямоугольник.
2) Если четырехугольник - квадрат, то он прямоугольник.
3) Четырехугольник является прямоугольником - это следствие того, что четырехугольник - квадрат.
4) Для того чтобы четырехугольник был прямоугольником, достаточно, чтобы он был квадратом.
5) Для того чтобы четырехугольник был квадратом, необходимо, чтобы он был прямоугольником.
б) В данном высказывании так же, как и в а), можно выделить два предложения: Р(х) - «число делится на 5» и К(х) - «запись числа оканчивается нулем», причем второе является достаточным условием для первого. Поэтому имеет место следование: К(х) => Р(х), которое можно сформулировать так:
1) Из того, что запись числа оканчивается нулем, следует, что число делится на 5.
2) Всякое число, запись которого оканчивается нулем, делится на 5.
3) Если запись числа оканчивается нулем, то оно делится на 5.
4) Делимость числа на 5 - это следствие того, что его запись оканчивается нулем.
5) Для того чтобы запись числа оканчивалась нулем, необходимо, чтобы оно делилось на 5.
Как и любое высказывание, предложение А(х) => В(х) может быть истинным либо ложным. Но так как оно может быть (формулировано в виде «всякое А(х) есть В(х)», то его истинность устанавливается путем доказательства, а с помощью контрпримера - что оно ложно.
Задача 2. Определить значение истинности высказывания:
а) Если запись числа оканчивается цифрой 6, то число делится на 2.
б) Для того чтобы число делилось на 5, необходимо, чтобы п о запись оканчивалась нулем.
Решение, а) По всей видимости это высказывание истинное. Действительно, всякое число, запись которого оканчивается цифрой 6 - четное, а всякое четное число делится на 2.
Следовательно, число, запись которого оканчивается цифрой 6, делится на 2.
Мы убедились в истинности данного высказывания путем доказательства.
б) Если сформулировать данное высказывание в виде «из того, что число делится на 5, следует, что его запись оканчивается нулем», то сразу можно сказать, что оно ложное. И убедиться в этом можно при помощи контрпримера. Например, число 35 делится на 5, но его запись не оканчивается нулем.
С теоретико-множественной точки зрения высказывание А(х) => В(х) означает, что если ТА - множество истинности высказывательной формы А(х), а ТВ- множество истинности высказывательной формы В(х), то ТА 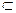 ТВ. Справедливо и обратное утверждение.
ТВ. Справедливо и обратное утверждение.
Этим фактом удобно пользоваться при установлении значения истинности высказывания А(х) => В(х).
Задача 3. Доказать, что из уравнения 3х(х - 2) = 0 следует уравнение 3х(х - 2)(х + 3) = 0, если уравнения заданы на множестве Z целых чисел.
Решение. Множество решений первого уравнения –Т2 = {0, 2}, множество решений второго - Т2 = {0, 2, -3}. Видим, что Т1 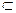 Т2. Следовательно, из уравнения 3х(х - 2) = 0 следует уравнение 3х(х - 2)(х + 3) = 0.
Т2. Следовательно, из уравнения 3х(х - 2) = 0 следует уравнение 3х(х - 2)(х + 3) = 0.
Рассмотрим две высказывательные формы А(х) - «число делится на 3» и В(х) - «сумма цифр в записи числа делится на 3». Из школьного курса математики известно, что если число делится на 3, то сумма цифр в записи этого числа разделится на 3, и наоборот. В этом случае говорят, что предложения А(х) и В(х) равносильны.
Определение. Предложения А (х) и В(х) равносильны, если из предложения А(х) следует предложение В(х), а из предложения В(х) следует предложение А (х).
Для обозначения отношения равносильности используется знак <=>. Соединяя две высказывательные формы А(х) и В(х) таким знаком, мы получаем высказывание А(х) <=> В(х), прочитать которое можно по-разному:
1) А(х) равносильно В(х).
2) А(х) тогда и только тогда, когда В(х).
3) А(х) - необходимое и достаточное условие для В(х).
4) В(х) - необходимое и достаточное условие для А(х).
Например, утверждение о том, что предложение «число делится на 3» и «сумма цифр в записи числа делится на 3» равносильны, можно сформулировать еще так:
- Число делится на 3 тогда и только тогда, когда сумма цифр в его записи делится на 3.
- Для того чтобы число делилось на 3, необходимо и достаточно, чтобы сумма цифр в его записи делилась на 3.
С теоретико-множественной точки зрения высказывание А(х) <=> В(х) означает, что если ТА - множество истинности высказывательной формы А(х), А(х) - множество истинности высказывательной формы В(х), то ТА = ТВ.
Задача 4. Доказать, что уравнения 3х(х - 2) = 0 и 3х(х - 2)(х + 3) = 0 равносильны на множестве целых неотрицательных чисел.
Решение. Множество решений первого уравнения Т1 = {0, 2}, множество решений второго, заданного на множестве целых неотрицательных чисел,
Т2 ={0, 2}. Число -3 множеству Т2 не принадлежит, потому что оно не является целым неотрицательным. Имеем, что Т1= Т2, следовательно, данные уравнения на множестве целых неотрицательных чисел равносильны.
Заметим, что мы рассматриваем понятия логического следования и равносильности для одноместных высказывательных форм. Для предложений, содержащих две и более переменных, эти понятия определяются аналогично.
Отметим также, что знак 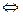 мы использовали раньше, в частности, рассматривая логическую структуру явных определений понятий. Мы установили, что ее можно представить в виде
мы использовали раньше, в частности, рассматривая логическую структуру явных определений понятий. Мы установили, что ее можно представить в виде 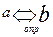 . Употребление знака
. Употребление знака 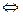 здесь не случайно. Дело в том, что определение, как говорят в математике, порождает два равносильных предложения, которые затем используются наряду с другими в доказательствах. Например, определение «квадратом называется прямоугольник, имеющий равные соседние стороны» порождает равносильные предложения: «если прямоугольник является квадратом, то в нем соседние стороны равны» и «если в прямоугольнике соседние стороны равны, то прямоугольник является квадратом». Использовать н доказательствах можно любое из этих двух.
здесь не случайно. Дело в том, что определение, как говорят в математике, порождает два равносильных предложения, которые затем используются наряду с другими в доказательствах. Например, определение «квадратом называется прямоугольник, имеющий равные соседние стороны» порождает равносильные предложения: «если прямоугольник является квадратом, то в нем соседние стороны равны» и «если в прямоугольнике соседние стороны равны, то прямоугольник является квадратом». Использовать н доказательствах можно любое из этих двух.
Знак 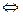 мы также использовали в записи правил построения
мы также использовали в записи правил построения
отрицания высказываний. Например, 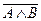
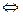
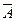
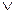
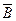 . В этом случае речь идет о равносильности высказываний определенной формы. При этом считают, что предложения равносильны, или они одновременно истинны, либо одновременно ложны. Другими словами, если их значения истинности совпадают при одинаковых наборах значений высказываний А и В.
. В этом случае речь идет о равносильности высказываний определенной формы. При этом считают, что предложения равносильны, или они одновременно истинны, либо одновременно ложны. Другими словами, если их значения истинности совпадают при одинаковых наборах значений высказываний А и В.
Дата добавления: 2017-02-13; просмотров: 5579;











