Конъюнкция и дизъюнкция высказывании.
Выясним смысл, который имеет в математике союз «и». Пусть А и В- произвольные высказывания. Образуем из них, с помощью союза «и», составное высказывание. Назовем его конъюнкцией и обозначим А  В (читают: «А и В»).
В (читают: «А и В»).
Определение. Конъюнкцией высказываний А и В называется высказывание А  В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из этих высказываний ложно.
В, которое истинно, когда оба высказывания истинны, и ложно, когда хотя бы одно из этих высказываний ложно.
Определение конъюнкции можно записать с помощью таблицы, называемой таблицей истинности.
| А | В | А  В В
|
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 и на 9», которое, как было установлено раньше, состоит из двух элементарных высказываний, соединенных союзом «и», т.е. является конъюнкцией. Так как первое высказывание истинно, а второе ложно, то, согласно определению конъюнкции, высказывание «число 28 делится на 7 и на 9» будет ложным.
Заметим, что данное определение конъюнкции не расходится с общепринятым пониманием союза «и». Действительно, если мы знаем, что каждое из предложений «сегодня идет снег» и «сегодня холодно» истинно, то мы будем считать истинным и предложение «сегодня идет снег и холодно». Если же одно из этих предложений или оба будут ложными, то и все предложение «сегодня идет снег и холодно» мы будем считать ложным.
Заметим также, что в обыденной речи конъюнкция может выражаться не только с помощью союза «и», но и другими, например, «а», «но», «однако», «не только..., но и ...». Например: «Число 15 делится не только на 3, но и на 5».
Выясним теперь, какой смысл имеет в математике союз «или».
Пусть А и В- произвольные высказывания. Образуем из них с помощью союза «или» составное высказывание. Назовём его дизъюнкцией и обозначим A v В (читают: «А или В»).
Определение. Дизъюнкцией высказываний А и В называется высказывание A 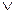 В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.
В, которое истинно, когда истинно хотя бы одно из этих высказываний, и ложно, когда оба высказывания ложны.
Таблица истинности дизъюнкции имеет вид:
| А | В | А 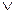 В В
|
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Используя данное определение, найдем значение истинности высказывания «число 28 делится на 7 или на 9». Так как это предложение является дизъюнкцией двух высказываний, одно из которых истинно, то, согласно определению, оно истинно.
Из определения дизъюнкции следует, что в математике союз «или» используется как неразделительный, т.е. допускается возможность одновременного выполнения обоих условий. Так, высказывание «15 кратно 3 или 5», согласно определению, считается истинным, поскольку оба высказывания «15 кратно 3» и «15 кратно 5» истинны.
Образование составного высказывания с помощью логической связки называется логической операцией. Операция, соответствующая союзу «и», называется конъюнкцией; операция, соответствующая союзу «или»,- дизъюнкцией. Заметим, что названия логических операций и их результаты (составные предложения) называются одинаково.
Определения конъюнкции и дизъюнкции можно обобщить на t составляющих их высказываний.
Конъюнкцией t высказываний называется предложение вида А1  А2
А2  ...
...  Аt которое истинно тогда и только тогда, когда истинны все составляющие его высказывания.
Аt которое истинно тогда и только тогда, когда истинны все составляющие его высказывания.
Дизъюнкцией t высказываний называется предложение вида A1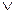 А2
А2 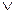 ...
... 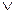 Аt которое ложно тогда и только тогда, когда ложны все составляющие его высказывания.
Аt которое ложно тогда и только тогда, когда ложны все составляющие его высказывания.
Дата добавления: 2017-02-13; просмотров: 6192;











