Решение задач на распознавание объектов

С введением понятия конъюнкции и дизъюнкции высказывательных форм появились условия для рассмотрения вопросов, связанных с решением определенного вида задач, так называемых задач на распознавание объектов.

В задачах на распознавание требуется ответить на вопрос: принадлежит тот или иной объект объему данного понятия или не принадлежит. Примером такой задачи может быть следующая: «Установите, какие из фигур на рисунке 1 являются квадратами, а какие нет».

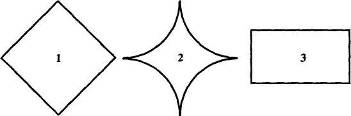
Рис. 1

Решают такие задачи, используя определение соответствующего понятия. При этом важно понимать, что если понятие а определено через родовое понятие с и видовое отличие Р, то его объем А можно представить в таком виде: А = {х | х С и Р(х)}. Эта запись показывает, что характеристическое свойство элементов, принадлежащих объему понятия а, представляет собой конъюнкцию двух свойств:

1) принадлежности объекта х объему С родового понятия (х С);

2) свойства Р(х).

Это означает, что объект х будет принадлежать объему понятия а тогда и только тогда, когда он (этот объект) содержится в объеме родового понятия и обладает свойством Р. Поэтому распознавание производится по следующему правилу:

1. Проверяем, принадлежит ли объект х объему родового понятия, т.е. истинно ли высказывание х С.

2. Если окажется, что х 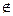С, то проверку прекращаем и делаем вывод, что объект х не принадлежит объему понятия а, т.е. x 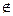A.

3. Если х С, то продолжаем проверку и выясняем, обладает ли объект х свойством Р.

4. Если объект х обладает свойством Р, то делаем вывод о его принадлежности объему понятия а, т.е. утверждаем, что х А.

5. Если окажется, что объект х не обладает свойством Р, то делаем вывод, что объект х не принадлежит объему понятия а, т.е. х 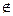А.

Выясним, например, какие из фигур на рисунке 1 являются квадратами. Будем пользоваться таким определением: «Квадратом называется прямоугольник, у которого соседние стороны равны». Из него следует, что для того, чтобы фигура была квадратом, она должна обладать двумя свойствами: «быть прямоугольником» и «иметь равные соседние стороны».

Фигура 1 является квадратом, так как это прямоугольник, соседние стороны которого равны.

Фигура 2 не является квадратом, так как это не прямоугольник.

Фигура 3 - прямоугольник, но соседние стороны в нем не равны. Следовательно, ее нельзя назвать квадратом.

Мы рассмотрели самый простой случай решения задачи на распознавание, когда видовое отличие в определении понятия состояло только из одного свойства. Но нередки и такие определения, в которых видовое отличие состоит из нескольких свойств, связанных между собой союзами «и», «или».

Если видовое отличие представляет собой конъюнкцию свойств, т.е. Р = Р₁ Р₂ ... Р_n, то распознавание проводится по следующему правилу: проверяют поочередно наличие у объекта каждого из свойств Р₁, Р₂, … Р_n; если окажется, что он не обладает каким-либо из этих свойств, то проверку прекращают и делают вывод о том, что объект не обладает свойством Р; если же окажется, что все свойства Р₁, Р₂, … Р_n присущи данному объекту, то заключают, что объект обладает свойством Р.

Выясним, например, в каком случае луч BD является биссектрисой угла ABC (рис. 34). Воспользуемся таким определением биссектрисы угла: «Биссектрисой угла называется луч, выходящий из вершины угла и делящий этот угол пополам». Из него следует, что для того, чтобы луч был биссектрисой угла, он должен обладать двумя свойствами: «выходить из вершины угла» и «делить этот угол пополам».

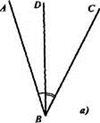
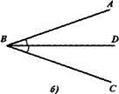
Рис.2

Луч BD на рисунке 2а не является биссектрисой угла ABC, поскольку он не делит данный угол пополам.

Луч BD на рисунке 2б биссектриса угла ABC, так как он выходит из вершины этого угла и делит его пополам.

Если видовое отличие представляет собой дизъюнкцию свойств Р = P₁v P₂v ...v Р_n, проверка проводится до тех пор, пока не будет установлено, что хотя бы одно из свойств присуще данному объекту, на основании чего заключают, что он обладает свойством Р. Если же окажется, что объект не обладает ни одним из свойств Р₁, Р₂, … Р_n, то приходят к выводу, что он не обладает свойством Р.