Конъюнкция и дизъюнкция высказывательных форм
В математике рассматривают не только конъюнкцию и дизъюнкцию высказываний, но и выполняют соответствующие операции над высказывательными формами.
Конъюнкцию одноместных высказывательных форм А(х) и В(х), заданных на множестве Х, обозначают А(х)  В(х). С появлением этого предложения возникает вопрос, как на его множество истинности, зная множества истинности высказывательных форм А(х) и В(х). Другими словами, при каких значениях х из области определения X высказывательная форма А(х)
В(х). С появлением этого предложения возникает вопрос, как на его множество истинности, зная множества истинности высказывательных форм А(х) и В(х). Другими словами, при каких значениях х из области определения X высказывательная форма А(х)  В(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить ТА- множество истинности предложения А(х), ТВ- множество истинности предложения В(х), а множество истинности их конъюнкции ТА
В(х) обращается в истинное высказывание? Очевидно, что это возможно при тех и только тех значениях х, при которых обращаются в истинное высказывание обе высказывательные формы А(х) и В(х). Если обозначить ТА- множество истинности предложения А(х), ТВ- множество истинности предложения В(х), а множество истинности их конъюнкции ТА  В, то, по всей видимости, ТА
В, то, по всей видимости, ТА  В = ТА
В = ТА 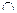 ТВ.
ТВ.
Докажем это равенство.
1. Пусть а - произвольный элемент множества X и известно, что а  ТА
ТА  В. По определению множества истинности это означает, что высказывательная форма А(х)
В. По определению множества истинности это означает, что высказывательная форма А(х)  В(х) обращается в истинное высказывание при х = а, т е. высказывание А(а)
В(х) обращается в истинное высказывание при х = а, т е. высказывание А(а)  В(а) истинно. Так как данное высказывание конъюнкция, то, по определению конъюнкции, получаем, что каждое из высказываний А (а) и В(а) также истинно. Это означает, что а
В(а) истинно. Так как данное высказывание конъюнкция, то, по определению конъюнкции, получаем, что каждое из высказываний А (а) и В(а) также истинно. Это означает, что а  ТА и а
ТА и а  ТВ. Следовательно, по определению пересечения множеств, а
ТВ. Следовательно, по определению пересечения множеств, а  ТА
ТА 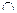 ТВ. Таким образом, мы показали, что
ТВ. Таким образом, мы показали, что
ТА  В
В 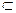 ТА
ТА 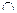 ТВ,
ТВ,
2. Докажем обратное утверждение. Пусть а - произвольный элемент множества X и известно, что а  ТА
ТА 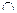 ТВ. По определению пересечения множеств это означает, что а
ТВ. По определению пересечения множеств это означает, что а  ТА и а
ТА и а  ТВ, откуда получаем, что А(а) и В(а) - истинные высказывания, поэтому конъюнкция высказываний А(а)
ТВ, откуда получаем, что А(а) и В(а) - истинные высказывания, поэтому конъюнкция высказываний А(а)  В(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)
В(а) также будет истинна. А это означает, что элемент а принадлежит множеству истинности высказывательной формы А(х)  В(х), т.е. а е Т
В(х), т.е. а е Т  АА
АА  В. Таким образом, мы доказали, что ТА
В. Таким образом, мы доказали, что ТА 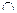 ТВ
ТВ 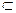 ТА
ТА  В.
В.
Из 1 и 2 в силу определения равных множеств вытекает справедливость равенства ТА  В = ТА
В = ТА 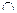 ТВ, что и требовалось доказать.
ТВ, что и требовалось доказать.
Заметим, что полученное правило справедливо и для высказывательных форм, содержащих более одной переменной.
Приведем пример использования этого правила. Найдем множество истинности конъюнкции двух неравенств 1х > 10 и 4 + х < 12, т.е. множество истинности предложения 2х> 10 и 4 + х< 12. Пусть Т1- множество решений неравенства 2х > 10, а Т2- множество решений неравенства 4 + х < 12. Тогда Т1 = (5, +∞), Т2 = ( - ∞, 8). Чтобы найти те значения х, при которых истинны оба неравенства, надо найти пересечение их множеств решений: Т1 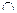 Т2 = (5,8).
Т2 = (5,8).
Видим, что выполнение этого задания свелось к решению системы неравенств. Вообще с точки зрения логики любая система неравенств есть конъюнкция неравенств, так же как и система уравнений есть конъюнкция уравнений.
Дизъюнкцию одноместных высказывательных форм А(х) и В(х) заданных на множестве X, обозначают A(x)vB(x). Это предложение будет обращаться в истинное высказывание при тех и только тех значениях х из области определения X, при которых обращается в истинное высказывание хотя бы одна из высказывательных форм, т.е. TAvB = ТА 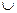 ТВ.
ТВ.
Доказательство этого равенства проводится аналогично рассмотренному выше.
Приведем пример использования этого правила. Решим, например, уравнение (х - 2)∙(х + 5) = 0. Известно, что произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Это означает, что данное уравнение равносильно дизъюнкции: x-2 = 0 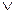 c + 5 = 0 и поэтому множество его решений может быть найдено как объединение множеств решений первого и второго уравнений, т.е. {2}
c + 5 = 0 и поэтому множество его решений может быть найдено как объединение множеств решений первого и второго уравнений, т.е. {2} 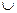 {-5} = {-5, 2}.
{-5} = {-5, 2}.
Заметим, что дизъюнкцию уравнений (неравенств) называют также совокупностью. Решить совокупность уравнений (неравенств) - это значит найти те значения переменных, при которых истинно хотя бы одно из уравнений (неравенств), входящих в нее.
Рассматривая конъюнкцию и дизъюнкцию высказывательных форм, мы установили их тесную связь с пересечением и объединением множеств.
С другой стороны, характеристические свойства элементов пересечения и объединения множеств А и В представляют собой соответственно конъюнкцию и дизъюнкцию характеристических свойств данных множеств:
А 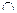 В={х│х
В={х│х  А и х
А и х  B},A
B},A 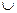 B={x│x
B={x│x  A или х
A или х  В}, причем каждое свойство представляет собой высказывательную форму.
В}, причем каждое свойство представляет собой высказывательную форму.
Дата добавления: 2017-02-13; просмотров: 4025;











