Структура теоремы. Виды теорем

<2 3 4 5 6 78>

Понятие логического исследования позволяет уточнить ряд вопросов, связанных с предложениями, которые в математике называют теоремами.

Теорема - это высказывание, истинность которого устанавливается посредством рассуждения (доказательства).

С логической точки зрения теорема представляет собой высказывание вида А 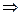В, где А и В - высказывательные формы с одной или несколькими переменными. Предложение А называют условием теоремы, а предложение В - её заключением.

Например, условием теоремы «если четырехугольник является прямоугольником, то в нем диагонали равны» является предложение «четырехугольник- прямоугольник», а заключением - предложение «в таком четырехугольнике диагонали равны».

В рассмотренном примере теорема была сформулирована с помощью слов «если ..., то ...». Но, как нам известно, утверждение А => В можно сформулировать и по-другому. Например, рассмотренную теорему можно сформулировать так: «во всяком прямоугольнике диагонали равны» или «для того, чтобы четырехугольник был прямоугольником, необходимо, чтобы его диагонали были равны». Есть и другие способы, но удобнее теорему формулировать в виде «если ..., то ...», поскольку сразу видно ее условие (что дано) и заключение (что надо доказать).

В математике кроме теорем используются предложения, называемые правилами и формулами. Выясним, чем они отличаются от теоремы.

Рассмотрим, например, такую теорему из школьного курса алгебры: «если а - любое число и n, k - натуральные числа, то справедливо равенство аⁿ∙а^k = аⁿ⁺^k. Условие данной теоремы - это предложение «а- любое число» и «n, k - натуральные числа». Заключение - это равенство аⁿ∙а^к = аⁿ⁺^k, справедливость которого надо доказать, исходя из данного условия.

Для того чтобы этой теоремой было удобнее пользоваться на практике, при выполнении различных преобразований ее формулируют в виде правила: «при умножении степеней с одинаковыми основаниями показатели складываются» или записывают только формулу аⁿ∙а^k = аⁿ⁺^k, опуская все условия, указанные в теореме. Такие упрощения позволяют быстрее запоминать правила и формулы. Эту особенность математического языка широко используют в начальном курсе обучении математике, но при этом формулируют различные утверждения сразу в виде правил или формул, опуская точные формулировки теорем (и, следовательно, опуская, по сути дела, условие теоремы). Но учитель, конечно, должен уметь разворачивать изучаемые в начальной школе правила (формулы) и формулировать соответствующие им теоремы. Иначе возможны ошибки как содержательного, так и логического характера. Рассмотрим, например, изучаемое в начальном курсе математики правило деления суммы на число: «для того, чтобы разделить сумму на число, можно разделить на это число каждое из слагаемых и полученные результаты сложить». К этой словесной формулировке правила иногда добавляют формулу: (а + b):с = а:с + b:с.

Так как этот материал изучают в начальной школе, то надо отчетливо понимать, что числа а, b и с могут быть только целыми неотрицательными, причем с≠0. Кроме того, воспользоваться правой частью этого равенства можно при условии, что а кратно с и b кратно с.

Таким образом, теорема, лежащая в основе правила деления суммы на число, может быть сформулирована следующим образом: «Если а, b и с - целые неотрицательные числа (с≠0) и а кратно с и b кратно с, то разделить сумму а + b на число с можно, разделив на это число каждое из слагаемых».

Если воспользоваться символами, то условие и заключение этой теоремы можно записать так:

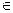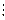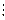условие: а, b, с Zo, с≠0; а с, b с

заключение: (а + b):с=а:с + b:с.

Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если В, то А», которое называют обратным данному. Однако не всегда это предложение является теоремой. Рассмотрим, например, теорему: «если четырехугольник является прямоугольником, то в нем диагонали равны». По-

строим предложение, обратное данному: «если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником». Это высказывание ложное, в чем можно убедиться, приведя контрпример: в равнобедренной трапеции диагонали равны, но трапеция не является прямоугольником.

Рассмотрим теперь теорему «в равнобедренном треугольнике углы при основании равны». Обратное ей предложение таково: «если в треугольнике углы при основании равны, то этот треугольник - равнобедренный». Оно, как известно, истинное и поэтому является теоремой. Ее называют теоремой, обратной данной.

Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не А, то не В», которое называют противоположным данному. Но не всегда это предложение является теоремой. Например, предложение, противоположное теореме «если четырехугольник является прямоугольником, то в нем диагонали равны», будет ложным: «если четырехугольник не является прямоугольником, то в нем диагонали не равны».

В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной.

Таким образом, если для теоремы А 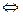В сформулировать обратное или противоположное предложения, то их надо доказывать (и тогда их можно называть соответственно обратной и противоположной теоремами) или опровергать.

Для всякой теоремы вида «если А, то В» можно сформулировать предложение «если не В, то не А», которое называют обратным противоположному. Например, для теоремы «если четырехугольник является прямоугольником, то в нем диагонали равны» предложение, обратное противоположному, будет таким: «если в четырехугольнике диагонали не равны, то он (четырехугольник) не является прямоугольником». Это, как известно, предложение истинное и, следовательно, является теоремой. Ее называют обратно противоположной данной.

Вообще для каких бы теорем мы ни формулировали предложения, обратные противоположным, они всегда будут теоремами, потому что имеется следующая равносильность

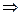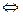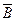
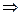(А В) =( Ā).

Эту равносильность называют законом контрапозиции. Мы принимаем его без доказательства. Согласно этому закону, предложение, обратно противоположное какой-либо теореме, также является теоремой, и, значит, вместо данной теоремы можно доказывать теорему, обратно противоположную данной.

Кроме того, из закона контрапозиции следует, что предложение, обратное данному, и предложение, противоположное данному, одновременно истинны либо одновременно ложны. Поэтому, рассматривая их, достаточно доказать (или опровергнуть) какое-нибудь одно; тем самым будет доказано (опровергнуто) и второе.

Заметим, что если для данной теоремы А 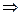В существует обратная В 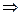А, то их можно объединить в одну А 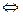В, и тогда в формулировке будут использоваться слова «необходимо и достаточно», «тогда и только тогда, когда». Например, объединение теоремы «в равнобедренном треугольнике углы при основании равны» и «если в треугольнике углы при основании равны, то треугольник - равнобедренный» в одну, получим теорему: «треугольник будет равнобедренным тогда и только тогда, когда в нем углы при основании равны».

Можно сформулировать ее иначе: «для того, чтобы треугольник был равнобедренным, необходимо и достаточно, чтобы в нем углы при основании были равны».

С другой стороны, если теорема имеет вид равносильности А 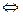В, то это значит, что она состоит из двух взаимно обратных теорем А 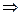В и В 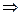А и, следовательно, ее доказательство сводится к доказательству двух указанных теорем.

Заметим также, что если условие или заключение данной теоремы представляет собой конъюнкцию или дизъюнкцию, то, чтобы получить предложение, противоположное данному, нужно учитывать правила построения отрицания конъюнкции и дизъюнкции. Например, дана теорема «если число делится на 3 и 4, то оно делится на 12». Предложение, противоположное данному, можно сформулировать так: «если число не делится на 12, то оно не делится на 3 или не делится на 4».

<2 3 4 5 6 78>

Дата добавления: 2017-02-13; просмотров: 9730;