Локальная и интегральная формулы Муавра-Лапласа

Для схемы Бернулли при больших n применимы приближенные формулы.

Локальная формула Муавра-Лапласа:

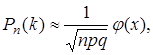(2.9)

где .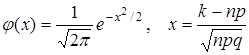

Интегральная формула Муавра-Лапласа:

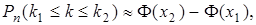(2.10)

где 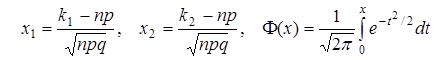– Функция Лапласа.

Замечание 2.3 Формулы (2.9) и (2.10) можно применять при больших значениях n и не очень малых p и q. В [Чудесенко] рекомендуется применять их при npq > 9, а в [Кремер] – при npq ³ 20.

Замечание 2.4Для нахождения значений по формулам (2.9), (2.10) существуют таблицы [Ефимов], [Чудесенко].

Задача 2.4Вероятность рождения мальчика в регионе составляет р = 0.51. Какова вероятность того, что из 500 новорожденных в регионе мальчиков не менее 250?

Решение. Имеет место схема Бернулли с параметрами: n =500, p =0.51, q= 0.49.

npq =51×0.49=24.99 >20, значит, применима интегральная формула Муавра-Лапласа.

.

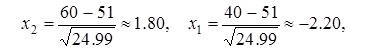
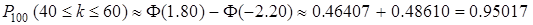Значения функции Лапласа взяты из таблицы II [Чудесенко].

Точное значение вероятности равна 0.9611386… . Погрешность составляет около 0.01. Относительно большая погрешность объясняется, по-видимому, небольшим значением n.

Для сравнения погрешностей формул Пуассона и Муавра-Лапласа вычислим по формуле (2.9) вероятность из задачи п. 2.2.

,

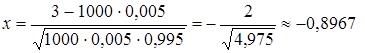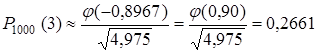(таблица I в [Чудесенко]).

Получилась очень большая погрешность по сравнению с результатом п. 2.7, т.е. в этой задаче локальная формула Муавра-Лапласа не приемлема.