Формула полной вероятности

Пусть для событий H₁, H₂ , …, H_n (n ³ 2) выполнены два условия:

1) они попарно несовместны и имеют ненулевые вероятности;

2) .

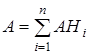Тогда верна формула полной вероятности:

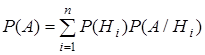(2.4)

События H₁, H₂ , …, H_n называются гипотезами, а смысл равенства 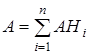состоит в том, что событие А может произойти только с одним из гипотез.

Выведем эту формулу. Так как события АН_i (i = 1, …, n ) несовместны, то по формуле сложения вероятностей и формуле (2.3) имеем

,

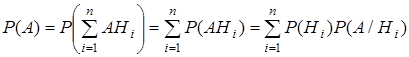что и требовалось доказать.

Задача 2.1 В магазин поступили однотипные телевизоры с 1-го завода 10 шт., со 2-го завода 15 шт. Вероятность изготовить бракованный телевизор на 1-м заводе равна 0,1, на 2-м – 0,2. Случайно отобрали один из поступивших телевизоров. Какова вероятность того, что он бракованный?

Решение. Введем события:

А – «Выбранный телевизор оказался бракованным»,

Н₁– «Выбранный телевизор изготовлен на 1-м заводе»,

Н₂– «Выбранный телевизор изготовлен на 2-м заводе»,

Гипотезы Н₁, Н₂ несовместны и событие А может произойти только с одним из них. Значит можно применить формулу полной вероятности.

P(Н₁)=10/25 = 2/5=0,4; P(A/Н₁) = 0,1;

P(Н₂)=15/25 = 3/5=0,6; P(A/Н₂) = 0,2.

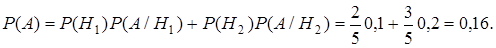
Формула Байеса

При выполнении для гипотез H₁, H₂ , …, H_n и события А условий 1) и 2) п. 2.3 верна формула Байеса:

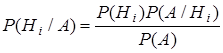, i = 1, …, n. (2.5)

По этим формулам вычисляются так называемые апостериорные вероятности гипотез, то есть вероятности гипотез после того как событие А произошло. Безусловные вероятности гипотез Р(Н_i) называются априорными.

Задача 2.2При условиях задачи из 2.1 найти вероятность гипотез Н₁, Н₂ ,если известно, что отобранный телевизор оказался бракованным.

Решение.Используя результаты вычислений из решения задачи 2.1, по формуле Байеса имеем:

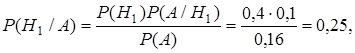
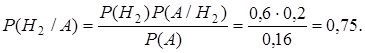
Как видим, апостериорная вероятность гипотезы Н₁ уменьшилась по сравнению априорной вероятностью. Объяснение простое: поскольку на первом заводе брака делается в два раза меньше, чем на втором, а выбранный телевизор оказался бракованным, то, естественно, вероятность того, что он из 1-го завода уменьшится.