Схема и формула Бернулли
Схема Бернулли – это независимое многократное повторение одного и того же опыта, который имеет два противоположных события: успех и неудача.
Введем обозначения:
p – вероятность успеха,
q = 1– p – вероятность неудачи,
n – число повторения опыта (n ³ 2),
k – число успехов в n повторениях опыта (k = 0,1, …, n).
Вероятность появления k раз успеха в n независимых повторениях опыта вычисляется по формуле Бернулли:
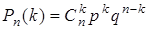 , (2.6)
, (2.6)
где 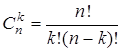 – число сочетаний из n по k.
– число сочетаний из n по k.
Вывод формулы Бернулли. Результатом n независимых повторений опыта является произведение n успехов и неудач в совокупности: 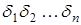 , где
, где 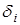 – либо успех, либо неуспех. Если в этом произведении k успехов и n–k неудач, то по формуле умножения вероятностей
– либо успех, либо неуспех. Если в этом произведении k успехов и n–k неудач, то по формуле умножения вероятностей
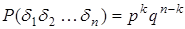 .
.
Два события вида 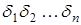 , имеющие ровно k успехов отличаются тем, что успехи располагаются на разных местах. Если выписать подряд номера мест, соответствующие успехам, то получим сочетание из n по k. Таким образом, событий вида
, имеющие ровно k успехов отличаются тем, что успехи располагаются на разных местах. Если выписать подряд номера мест, соответствующие успехам, то получим сочетание из n по k. Таким образом, событий вида 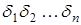 , имеющих ровно k успехов, ровно
, имеющих ровно k успехов, ровно 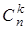 . Следовательно, по формуле сложения вероятностей
. Следовательно, по формуле сложения вероятностей
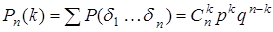 ,
,
где суммирование осуществляется по всем событиям вида 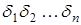 , имеющим ровно k успехов.
, имеющим ровно k успехов.
Пример 2.1. Пятикратное подбрасывание монеты является схемой Бернулли с параметрами n = 5, p =0.5, q = 0.5. По формуле Бернулли
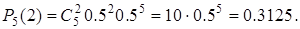
Пример 2.2. В аппаратуре работают независимо 1000 однотипных элементов. Вероятность выхода каждого из них за время работы T равна p = 0.005. Эту ситуацию можно рассматривать как схему Бернулли с n = 1000, p =0.005, q = 0.995. Обратите внимание на то, что успехом здесь является “негативное” событие – “Элемент вышел из строя за время работы T”.
По формуле Бернулли 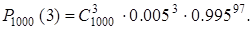 Нетрудно понять, что вычисление этого выражения затруднительно. Поэтому необходимы приближенные формулы для вычисления вероятностей
Нетрудно понять, что вычисление этого выражения затруднительно. Поэтому необходимы приближенные формулы для вычисления вероятностей 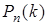 .
.
Дата добавления: 2017-02-13; просмотров: 1467;











