Независимость событий.
Условная вероятность
Пусть имеется вероятностное пространство (W,U, P). Рассмотрим два события A и B, причем P(B)>0.
Определение. Условной вероятностью события A при условии, что событие B произошло, называется число
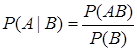 . (2.1)
. (2.1)
Условную вероятность еще обозначают PB(A). Фактически условная вероятность при условии выполнения события В рассматривается в новом вероятностном пространстве, где “комплексу условий проведения опыта” (см. начало п.1.1) добавляется еще одно условие, что событие В произошло. Тогда новое пространство элементарных событий будет подмножеством W, алгебра событий и вероятности изменятся.
Пример. Рассмотрим опыт К1 событие А – “выпало число, большее трех“. Вероятность Р(А) = 3/6 = 1/2. Пусть событие В – “выпало четное число” произошло. Тогда пространством элементарных событий в новых условиях является {2, 4, 6}. Вероятность события А при условии, что событие B произошло, равно по классическому определению вероятности 2/3, так как число всех элементарных событий в новом пространстве элементарных событий равно 3 и два элементарных события 4 и 6 благоприятствуют событию А. Теперь эту условную вероятность вычислим по определению:
В = {2, 4, 6} Þ Р(В) = 3/6 = 1/2; AB = {4, 6} Þ Р(АВ) = 2/6 = 1/3.
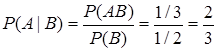 .
.
Как видно, результаты совпали.
Независимость событий.
Определение.Два события A и B называются (вероятностно) независимыми, если
Р(АВ) = Р(А)Р(В) (2.2)
Пусть P(B)>0, A и B независимы. Тогда в силу равенства (2.2) выполняется равенство 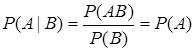 . Из этого следует, что если события A и B независимы, то вероятность Р(А) не зависит от того, произошло ли событие В или нет.
. Из этого следует, что если события A и B независимы, то вероятность Р(А) не зависит от того, произошло ли событие В или нет.
В теории вероятности применяется принцип: если события А и В причинно независимы, то они независимы вероятностно.
Докажите утверждение: если события А и В независимы, то независимы пары событий А и 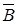 , В и
, В и 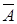 .
.
Теперь определим понятие независимости нескольких событий.
Определение. События A1, A2 , …, Аn (n ³ 2) называются независимыми (в совокупности), если для любого сочетания по k (2 £ k £ n) из этих событий выполняется равенство
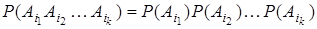 .
.
Дата добавления: 2017-02-13; просмотров: 2227;











