Исходные положения (аксиомы) статики

Основные положения (или аксиомы), из которых исходят при решении задач статики, можно сформулировать следующим образом.

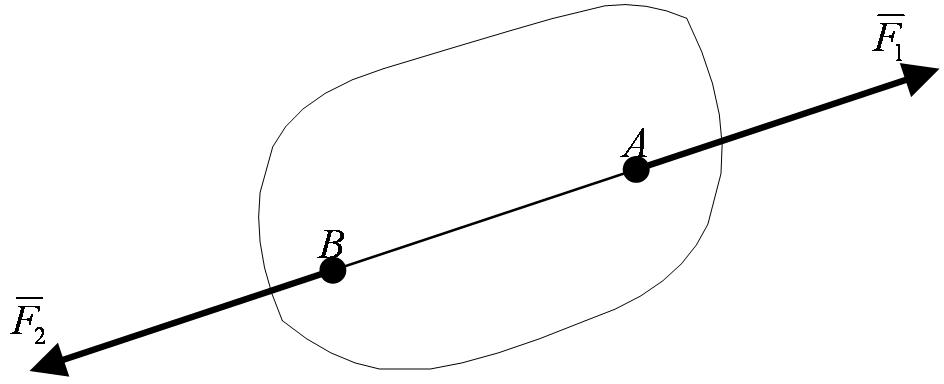
1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда, эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны (рисунок 1_2).

2. Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил.

Иными словами это означает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.

Следствие: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела (рисунок 1_3).

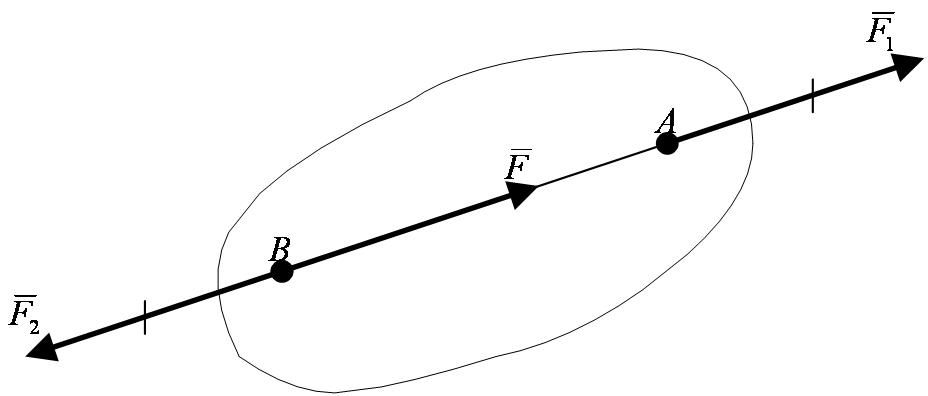
Полученный результат справедлив только для сил, действующих на абсолютно твердое тело. При инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникшие в ее частях внутренние усилия.

Еще два исходных положения относятся к общим законам механики.

Закон параллелограмма сил: две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.

Следовательно, при определении внутренних усилий переносить точку приложения силы вдоль линии действия нельзя.

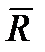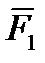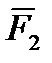Вектор , равный диагонали параллелограмма, построенного на векторах и (рисунок 1_4), называется геометрической суммой век торов 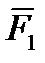и 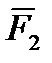, т.е. .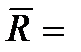

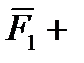
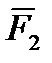Следовательно, закон параллелограмма сил можно еще сформулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.

В дальнейшем следует различать понятия суммы сил и их равнодействующей (рисунок 1_5).

Здесь сила 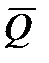является геометрической суммой, но не является равнодействующей сил 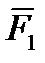и .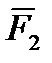

3акон равенства действия и противодействия:при всяком действии одного материального тела на другое имеет место такое же численно, но противоположное по направлению противодействие.

Этот закон является одним из основных законов механики. Из него следует, что если тело А действует на тело В с некоторой силой 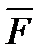то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но в противоположную сторону силой 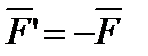(рисунок 1_6). Заметим, что силы 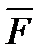и 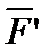, как приложенные к разным телам, не образуют уравновешенную систему сил.

Связи и их реакции

Термин несвободное тело.

Термин связь.

Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, будет действовать на нее с некоторой силойдавления на связь. Одновременно по закону о равенстве действия и противодействия связь будет действовать на тело с такой же по модулю, но противоположно направленной силой.

Термин реакция связи.

Значение реакции связи зависит от других действующих сил и наперед неизвестно. Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу.Когда связь может препятствовать перемещениям тела по нескольким направлениям, направление реакции такой связи тоже наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.

Рассмотрим подробнее, как направлены реакции некоторых основных видов связей.

1. Гладкая плоскость (поверхность) или опора

Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рисунок 1_7).

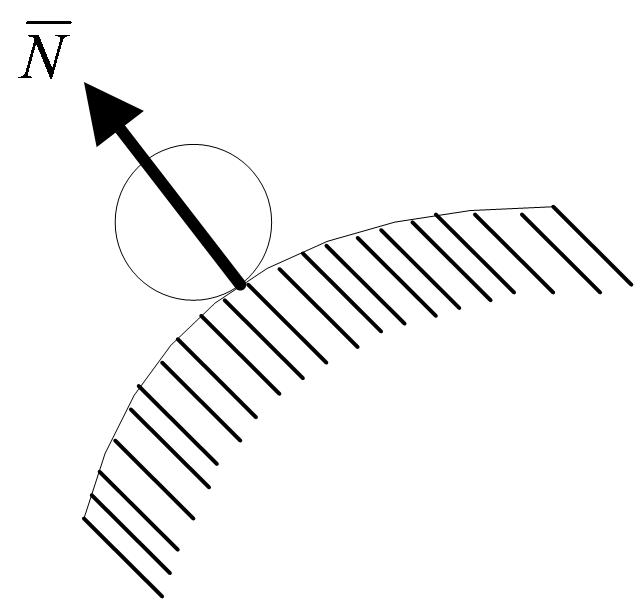
Поэтому реакция 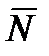гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рисунок 1_8),то реакция направлена по нормали к другой поверхности.

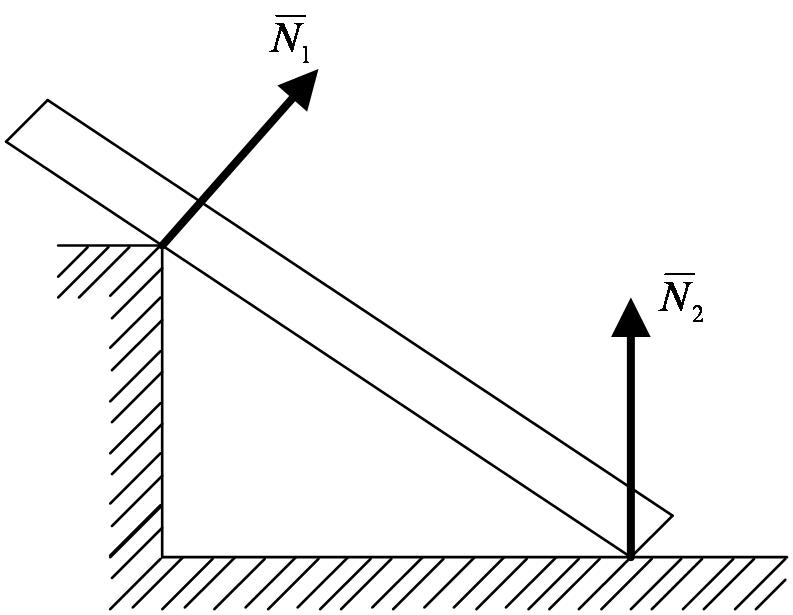
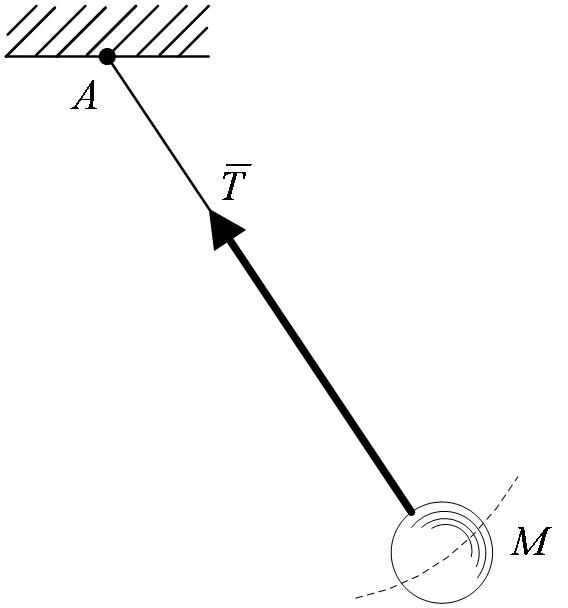
2. Нить

Связь, осуществленная в виде гибкой нерастяжимой нити (рисунок 1_9), не дает телу М удаляться от точки подвеса нити по направлению АМ. Поэтому реакция 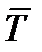натянутой нити направлена вдоль нити к точке ее подвеса.

3. Цилиндрический шарнир (подшипник)

Цилиндрический шарнир осуществляет такое соединение двух тел, при котором одно тело может вращаться по отношению к другому вокруг общей оси, называемой осью шарнира. Если тело АВ прикреплено с помощью такого шарнира к неподвижной опоре D (рисунок 1_10),

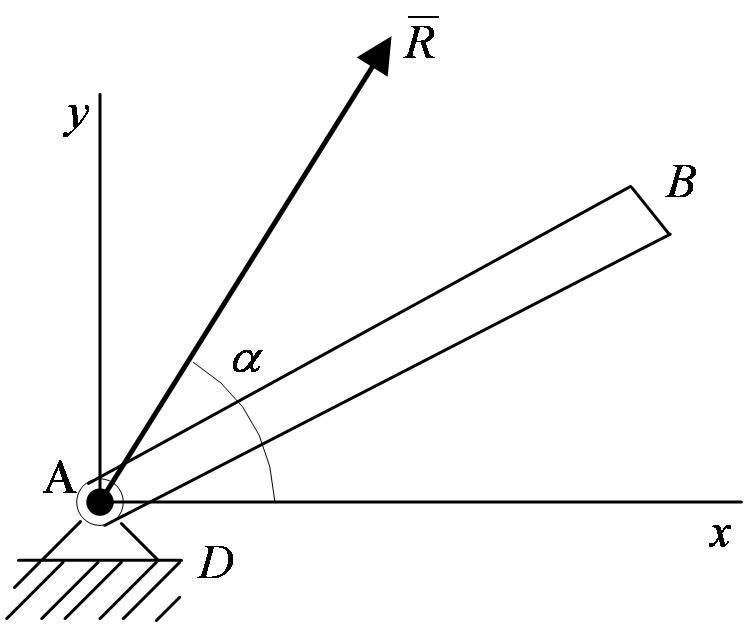
то точка A тела не может при этом переместиться ни по какому направлению, перпендикулярному оси шарнира. Следовательно, реакция цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси шарнира, т.е. в плоскости Аху. Для силы в этом случае наперед неизвестны ни ее модуль R, ни направление (угол ).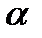

4. Сферический шарнир и подпятник

Тела, соединенные сферическим шарниром, могут как угодно поворачиваться одно относительно другого вокруг центра шарнира. Если тело прикреплено с помощью такого шарнира к неподвижной опоре (рисунок 1_11),

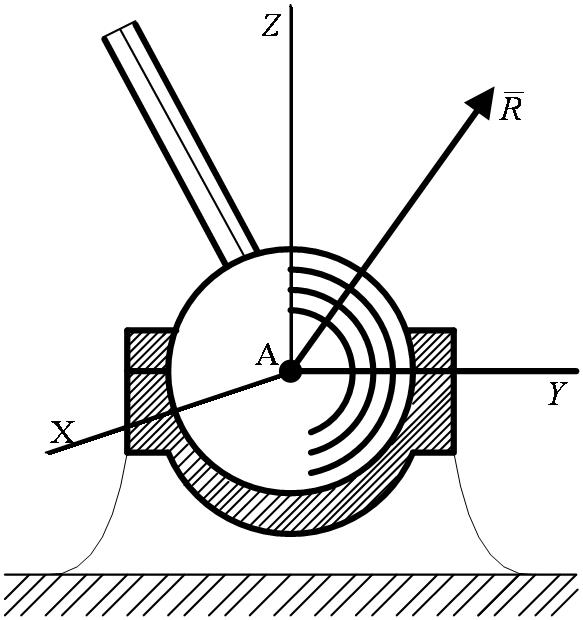
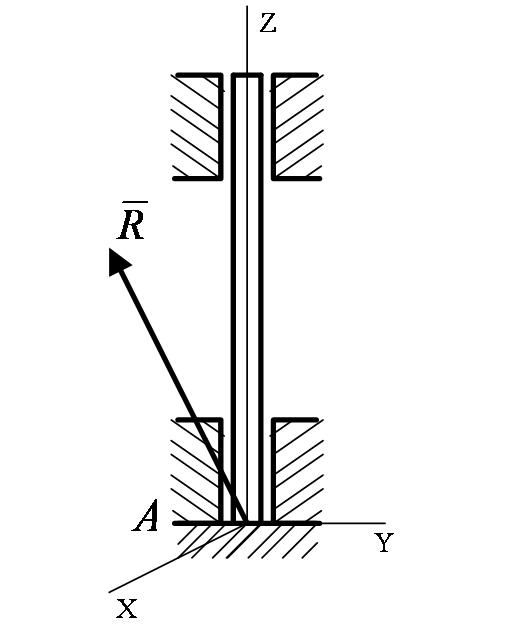
то точка А тела, совпадающая с центром шарнира, не может при этом совершить никакого перемещения в пространстве. Следовательно, реакция 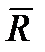сферического шарнира может иметь любое направление в пространстве. Для нее наперед неизвестны ни ее модуль R, ни углы с осями Ахуz.

Произвольное направление в пространстве может иметь и реакция 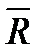подпятника (подшипника с упором), изображенного на рисунке 1_12.

5. Невесомый стержень

Термин невесомый стержень. Пусть для какого-нибудь находящегося в равновесии тела (конструкции) такой стержень, прикрепленный в точках А иВшарнирами, является связью (рисунок 1_13).

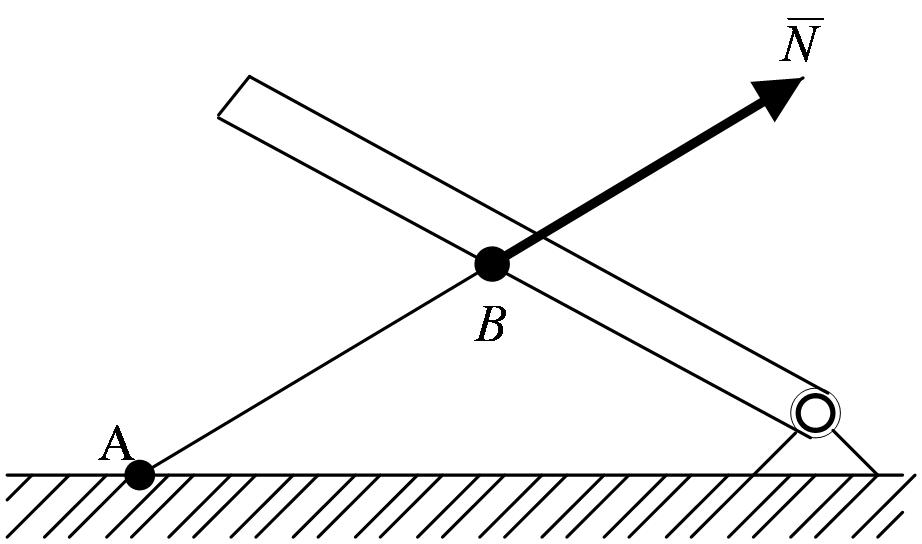
Стержень не дает перемещаться телу (конструкции) в направлении АВ, следовательно, реакция невесомого шарнирно прикрепленного прямолинейного стержня направлена вдоль оси стержня.

Если связью является криволинейный невесомый, стержень (рисунок 1_14),

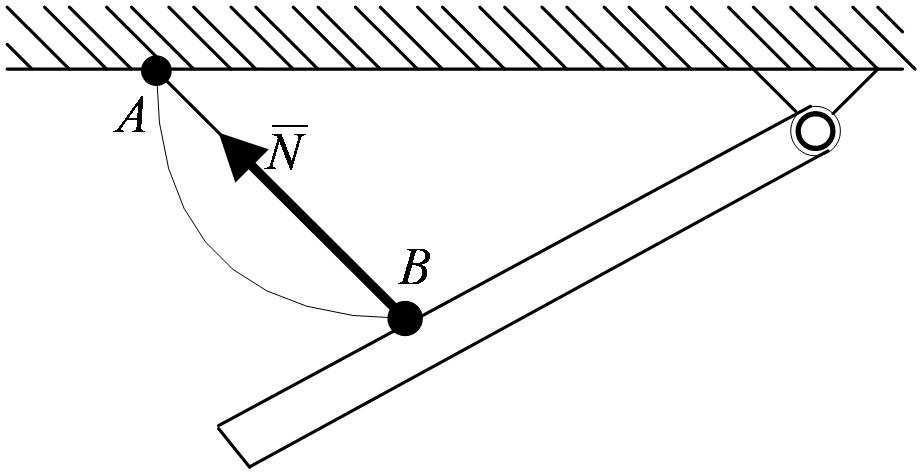
то аналогичные рассуждения приведут к выводу, что его реакция тоже направлена вдоль прямой АВ,соединяющей шарниры А и В.

При решении задач реакции связей обычно являются подлежащими определению неизвестными. Нахождение реакций имеет то практическое значение, что определив их, а тем самым определив по закону о действии и противодействии и силы давления на связи, получают исходные данные, необходимые для расчета прочности соответствующих частей конструкции.