Предмет механики. Значение механики в естествознании и технике. Исторические этапы развития механики.

Наука о механическом движении и механическом взаимодействии материальных тел и называется механикой. Круг проблем, рассматриваемых в механике, очень велик и с развитием этой науки в ней появился целый ряд самостоятельных областей, связанных с изучением механики твёрдых деформируемых тел, жидкостей и газов. К этим областям относятся теория упругости, теория пластичности, гидромеханика, аэромеханика, газовая динамика и ряд разделов так называемой прикладной механики, в частности: сопротивление материалов, статика сооружений, теория механизмов и машин, гидравлика, а также многие специальные инженерные дисциплины. Однако во всех этих областях наряду со специфическими для каждой из них закономерностями и методами исследования опираются на ряд основных законов или принципов и используются многие понятия и методы, общие для всех областей механики. Рассмотрение этих общих понятий, законов и методов и составляет предмет так называемой теоретической (или общей) механики.

В основе механики лежат законы, называемой законами классической механики (или законами Ньютона), которые установлены путем обобщения результатов многочисленных опытов и наблюдений и нашли подтверждение в процессе всей общественно-производствен­ной практики человечества.

По характеру рассматриваемых задач теоретическую механику разделяют на статику, кинематику и динамику. В статике излагается учение о силах и об условиях равновесия материальных тел под действием сил. В кинематике рассматриваются общие геометрические свойства движения тел. Наконец, в динамике изучается движение материальных тел под действием сил.

Возникновение и развитие механики как науки неразрывно связано с историей развития производительных сил общества, с уровнем производства и техники на каждом этапе этого развития.

В древние времена, когда запросы производства сводились главным образом к удовлетворению нужд строительной техники, начинает развиваться учение о так называемых простейших машинах (блок, ворот, рычаг, наклонная плоскость) и общее учение о равновесии тел (статика). Обоснование начал статики содержится уже в сочинениях одного из великих ученых древности Архимеда (287-212 г. до н. э.).

Развитие динамики начинается значительно позже. В XV-XVI столетиях возникновение и рост в странах Западной и Центральной Европы буржуазных отношений послужили толчком к значительному подъему ремесел, торговли, мореплавания и военного дела (появление огнестрельного оружия), а также к важным астрономическим открытиям. Все это способствовало накоплению большого опытного материала, систематизация и обобщение которого привели в XVII столетии к открытию законов динамики. Главные заслуги в создании основ динамики принадлежат гениальным исследователям Галилео Галилею (1564–1642) и Исааку Ньютону (1643–1727). В сочинении Ньютона «Математические начала натуральной философии», изданном в 1687 г., и были изложены в систематическом виде основные законы классической механики (законы Ньютона).

В XVIII в. начинается интенсивное развитие в механике аналитических методов, т. е. методов, основанных на применении дифференциального и интегрального исчислений. Методы решения задач динамики точки и твердого тела путем составления и интегрирования соответствующих дифференциальных уравнений были разработаны великим математиком и механиком Л. Эйлером (1707–1783). Из других исследований в этой области наибольшее значение для развития механики имели труды выдающихся французских ученых Ж. Даламбера (1717–1783), предложившего свой известный принцип решения задач динамики, и Ж. Лагранжа (1736–1813), разработавшего общий аналитический метод решения задач динамики на основе принципа Даламбера и принципа возможных перемещений. В настоящее время аналитические методы решения задач являются в динамике основными.

Кинематика, как отдельный раздел механики, выделилась лишь в XIX в. под влиянием запросов развивающегося машиностроения. В настоящее время кинематика имеет и большое самостоятельное значение для изучения движения механизмов и машин.

Условия равновесия тела существенно зависят от того, является ли это тело твердым, жидким или газообразным. В общем курсе механики рассматриваются обычно только задачи о равновесии твердых тел.

Все встречающиеся в природе твердые тела под влиянием внешних воздействий в той или иной мере изменяют свою форму – деформируются. Для обеспечения прочности различных инженерных сооружений и конструкций материал и размеры их частей подбирают так, чтобы деформации при действующих нагрузках были достаточно малы.

Терминабсолютно твердое тело. В дальнейшем при решении задач статики все тела рассматриваются как абсолютно твёрдые.

Термин сила.

Рассматриваемые в механике величины можно разделить на скалярные,т. е. такие, которые полностью характеризуются их числовым значением, и векторные,т. е. такие, которые помимо числового значения характеризуются еще и направлением в пространстве.

Сила – величина векторная. Ее действие на тело определяется:

1) числовым значением или модулем силы,

2) направлением силы,

3) точкой приложения силы.

Графически сила изображается направленным отрезком (рисунок 1_1).

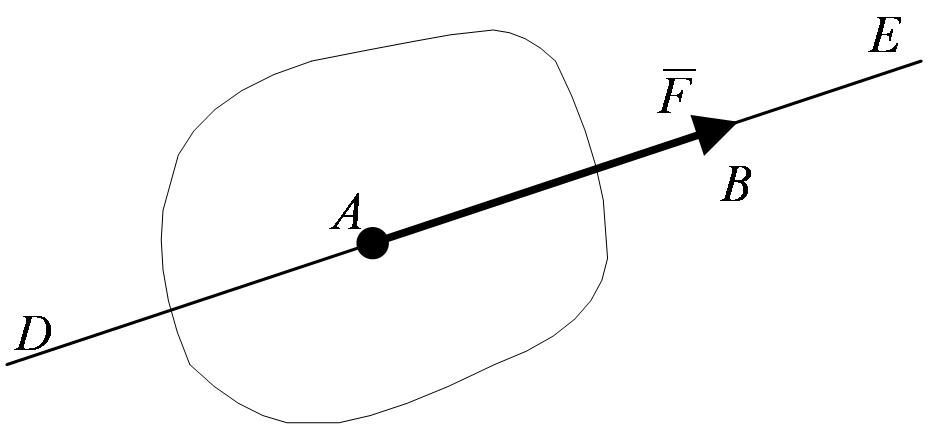
Здесь: А – точка приложения силы; DE – линией действия силы.

Условимся еще о следующих определениях:

1. Термин система сил. В зависимости от взаимного расположения линий действия сил, система сил может быть плоской или пространственной. Термин сходящиеся силы.

2. Термин свободное тело.

3. Термин эквивалентные системы сил.

4. Термин уравновешенная система сил.

5. Термин равнодействующая системы сил.

6. Силы, действующие на данное тело (или систему тел), можно разделить на внешние и внутренние, сосредоточенные и распределенные.

Термин внешние силы.

Термин внутренние силы.

Термин сосредоточенная сила.

Термин распределенные силы.

Задачами статики являются:

1) преобразование систем сил, действующих на твердое тело, в системы им эквивалентные, в частности приведение данной системы сил к простейшему виду;

2) определение условий равновесия систем сил, действующих на твердое тело.

Решать задачи статики можно или путем соответствующих геометрических построений (геометрический и графический методы), или с помощью численных расчетов (аналитический метод).