Лекция №2 Тема 1.2 Основные теоремы статики

Вопросы:

1.2.1. Векторное и графическое условие равновесия системы сходящихся сил. Теорема о трех силах.

1.2.2. Момент силы относительно точки и оси. Зависимость между ними.

1.2.3. Понятие о паре сил. Момент пары сил как вектор. Свойства пар сил. Теоремы о паре сил. Сложение пар сил, расположенных на плоскости и в пространстве. Условия равновесия системы пар сил.

1.2.4. Теоремы о параллельном переносе силы и приведении сил к заданному центру. Главный вектор и главный момент системы сил. Распределенные силы и равнодействующие распределенных сил.

Геометрический способ сложения сил

Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил.

Термин главный вектор. Как уже отмечалось, понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей.

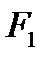Геометрическая сумма двух сил и 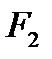находится по правилу параллелограмма (рисунок 1_15)

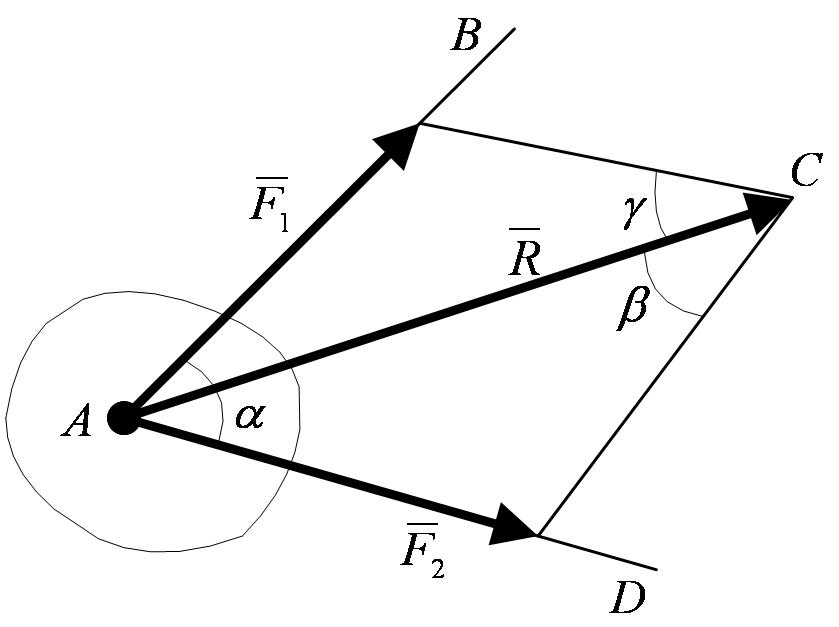
или построением силового треугольника (рисунок 1_16),

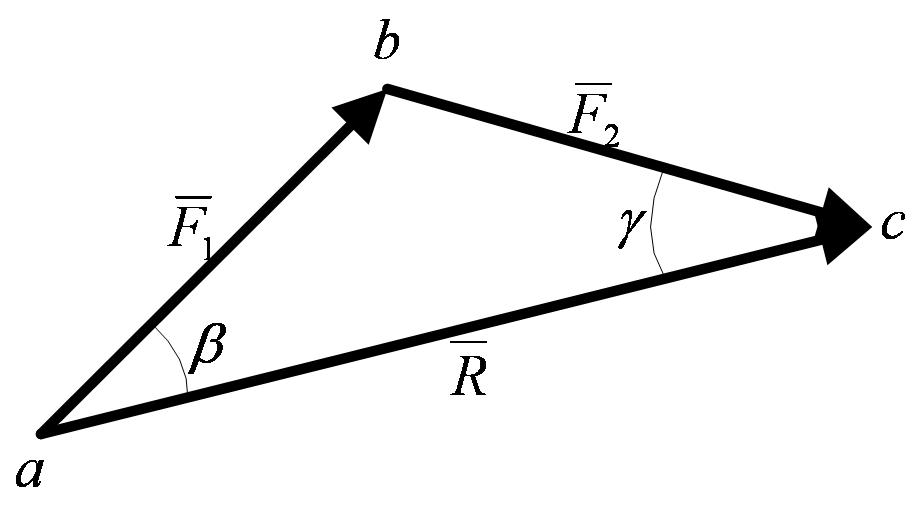
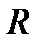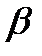изображающего одну из половин этого параллелограмма. Если угол между силами равен α, то модуль иуглы и 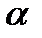, которые сила образует со слагаемыми силами, определяются по формулам:

	(1.1)
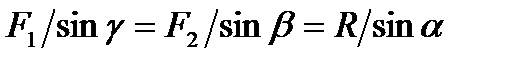
	(1.2)

Геометрическая сумма трех сил 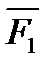, , 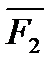, 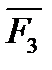не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда).

В справедливости этого убеждаемся, применяя последовательно правило параллелограмма (рисунок 1_17).

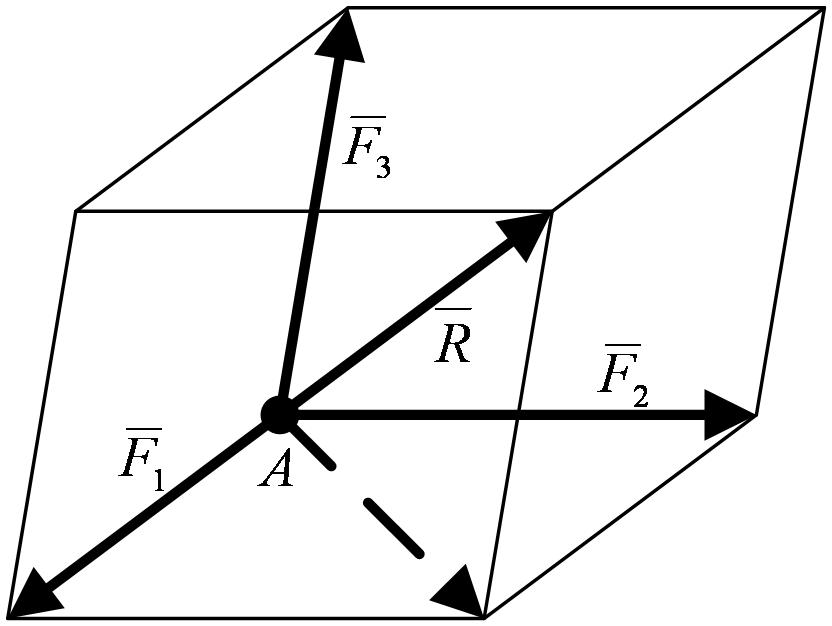
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным.

б)

Равнодействующая сходящихся сил

Рассмотрим систему сходящихся сил, т. е. сил, линии действия которых пересекаются в одной точке (рисунок 1_18).

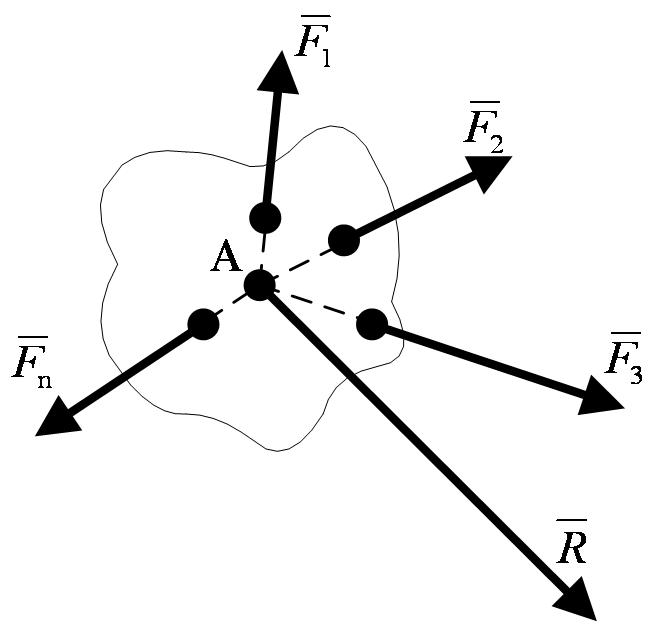
Так как сила, действующая на абсолютно твердое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рисунке 1_18в точке ).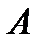

Последовательно применяя закон параллелограмма сил, придем к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия.

Следовательно, система сил 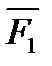, , 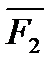. . . , 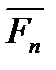, изображенных на рисунке 1_18,имеет равнодействующую, равную их главному вектору , найденному построением силового многоугольника,и приложенную в точке А.

Разложение сил

Разложить данную силу на несколько составляющих – значит найти такую систему нескольких сил, для которой данная сила является равнодействующей. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий. Рассмотрим два частных случая:

Задача о разложении силы по двум заданным направлениям сводится к построению такого параллелограмма, у которого разлагаемая сила является диагональю, а стороны параллельны заданным направлениям.

Задача о разложение силы по трем заданным направлениям является определенной, если заданные направления не лежат в одной плоскости, и сводится к построению такого параллелепипеда, у которого диагональ изображает заданную силу 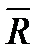, а ребра параллельны заданным направлениям.

Способом разложения можно в простейших случаях пользоваться для определения сил давления на связи. Для этого действующую на тело (конструкцию) заданную силу надо разложить по направлениям реакции связей, так как согласно закону о действии и противодействии сила давления на связь и реакция связи направлены вдоль одной и той же прямой.