Растяжение-сжатие стержней. Свойства материалов

3.1 Определение деформаций и напряжений при растяжении – сжатии

Возьмем стержень длиной 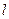, шириной 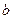и нанесем на его поверхность координатную сетку, т.е. линии вдоль продольной оси и перпендикулярно к ней. К торцам стержня приложим силы, на­правленные вдоль продольной оси. Стержень испытывает деформа­цию растяжения, длина его увеличивается на

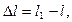
а ширина уменьшается на

,

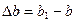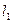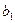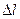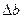здесь , — соответственно длина и ширина стержня после прило­жения сил. Величины и называют абсолютным удлинением (аб­солютной продольной деформацией) стержня и абсолютным сужением (абсолютной поперечной деформацией). Величину

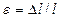
называют относительной линейной деформацией или относительным удлинением.

Соответственно 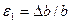называется относительной поперечной деформацией. Абсолютная величина отношения относительной попе­речной деформации 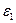к относительной продольной деформации 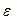называется коэффициентом поперечной деформации или коэффициен­том Пуассона:

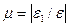
который характеризует упругие свойства материала, его способность к поперечным деформациям. Значение коэффициента Пуассона определяется экспериментально и для различных материалов колеблет­ся от нуля (для пробки) до 0,5 (для резины). Для большинства металли­ческих сплавов коэффициент Пуассона находится в пределах от 0,23 до 0,36 (для стали µ = 0,25 ... 0,33; для чугуна µ= 0,23 ... 0,27; для мед­ных сплавов µ = 0,31 ...0,36;для алюминиевых сплавов µ = 0,32...0,36).

Замечено, что прямые линии, перпендикулярные к продольной оси стержня, остаются прямыми и после деформаций, т.е. подтвер­ждается гипотеза плоских сечений (гипотеза Бернулли). Это позволяет утверждать, что деформации (удлинения) и, в соответствии с законом Гука, напряжения образующих стержня, параллельных оси, в любом поперечном сечении равны, т.е. деформации и напряжения во всех точках поперечного сечения одинаковы.

Определим внутренние силы в поперечном сечении, воспользовавшись методом сечений. Они уравновешивают внешнюю силу 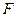, складываясь в равнодействующую внутренних сил 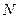. Из урав­нения равновесия в проекциях сил на продольную ось стержня опре­делим, что .

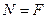Составляющая внутренних 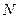сил направлена по нормали к попереч­ному сечению, поэтому в сечении действуют нормальные напряжения, определяемые с учетом равномерного распределения их по сечению:

,

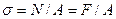где 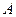— площадь поперечного сечения стержня.

При упругих деформациях справедлив закон Гука, устанавли­вающий линейную зависимость между напряжением и деформацией:

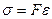
Коэффициент пропорциональности Е называют модулем упруго­сти материала (модулем Юнга). Он является физической постоянной материала, характеризует, как и коэффициент Пуассона, его упругие свойства и определяется опытным путем.

Формула для определения абсолютного удлинения стержня имеет вид:

.

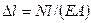Произведение 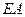характеризует сопротивляемость стержня удли­нению (сжатию) и называется жесткостью стержня при растяжении (сжатии).

Этой формулой можно пользоваться для определения абсолют­ной продольной деформации стержня длиной 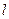при условии, что пло­щадь сечения стержня в пределах всей длины постоянна и продольная сила N во всех поперечных сечениях одинакова. Если параметры 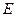, , 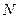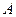по длине не постоянны, формула позволяет определять удли­нение только отдельного i-го участка стержня, а его полное удлинение определяется как алгебраическая сумма изменений длин участков.

Сжатие отличается от растяжения только направлением внешних сил. Принято считать внешние продольные силы, напряжения и де­формации при растяжении положительными, а при сжатии — отри­цательными. Зависимости для определения деформаций и напряже­ний при растяжении имеют место и при сжатии, но при сжатии длина стержня уменьшается, а поперечные размеры увеличиваются.

3.2 Механических свойств материалов. Диаграмма напряжений

При расчетах на прочность, жесткость и устойчивость свойства материалов определяются механическими характеристиками. Меха­нические характеристики могут быть получены в лабораторных усло­виях путем доведения образцов до разрушения или чрезмерной деформации. Испытания могут проводить на деформации растяжения, сжатия, кручения, изгиба при действии статической или переменной нагрузки.

Наибольшее распространение имеют испытания на растяжение статической нагрузкой, так как они наиболее просты и дают достаточ­ную информацию о поведении материала при других видах деформа­ции. На специальных машинах растягивают образцы (рис. 3.1, а), раз­меры которых ограничены стандартом, записывая автоматически зависимость изменения растягивающей силы 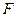от удлинения образца 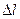, т.е. диаграмму растяжения в координатах .

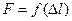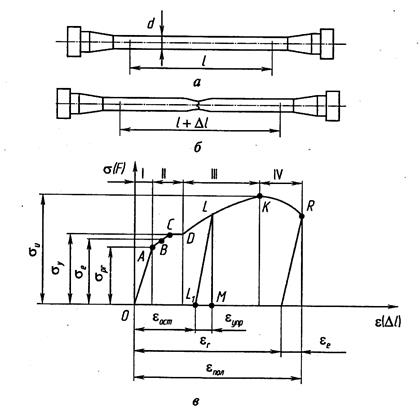
Рис. 3.1

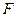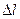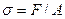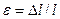Известно, что растягивающая сила и удлинение об­разцов из одного материала зависят от размеров образца. Чтобы мож­но было сравнить результаты испытаний образцов различных размеров, изготовленных из одинаковых материалов, диаграмму растяжения перестраивают в координатах и , где 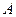— первоначаль­ная площадь сечения образцов; 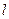— первоначальная длина рабочей части образца. Эту диаграмму 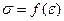называют диаграммой напряже­ний или условной диаграммой растяжения. Вид ее почти не зависит от абсолютных размеров используемых при испытании образцов, а определяется свойствами материала. Типовая диаграмма напряже­ний при растяжении образцов из пластичных материалов (рис. 3.1, в) характеризуется следующими участками. Участок ОА до некоторого напряжения 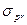называемого пределом пропорциональности, представ­ляет собой прямую линию. На этом участке справедлив закон Гука и абсолютная деформация 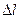прямо пропорциональна растягиваю­щему усилию 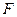, а относительная деформация 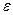— напряжению .

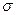После достижения предела пропорциональности 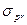деформации е растут не прямо пропорционально напряжениям 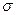, а быстрее. На­чиная с некоторой точки В, лежащей уже на криволинейном участке диаграммы, замечено появление незначительных (0,05 %) остаточных деформаций; до точки В деформации еще упругие. Точке В соответст­вует предел упругости материала 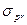— то наибольшее напряжение, до которого в материале появляются только упругие деформации. Пре­дел упругости практически совпадает с пределом пропорционально­сти, и эти величины обычно не разграничиваются. Например, для стали СтЗ предел пропорциональности 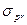≈ 210 МПа, а предел упру­гости 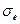= 220 МПа.

При дальнейшем увеличении нагрузки за точкой В появляются остаточные деформации. В точке С начинается процесс деформации металла без увеличения внешней 'нагрузки. Горизонтальный участок диаграммы называется площадкой текучести, а напряжение, соответ­ствующее данной точке, — пределом текучести .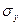

На участке DK (см. рис. 3.1, в) сопротивление деформированию начинает значительно возрастать при увеличении деформации. Уча­сток называется зоной упрочнения. Точка K диаграммы соответствует наибольшей нагрузке, а напряжение, соответствующее этой точке, называется пределом прочности 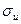или временным сопротивлением и обозначается при растяжении 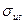. До точки K весь образец удлиняет­ся примерно одинаково, при превышении напряжения аи деформа­ция образца сосредоточивается в одном месте (локализуется). Это вы­зывает местное сужение поперечного сечения образца с образовани­ем так называемой шейки. Площадь сечения образца в шейке быстро уменьшается, и, как следствие, падает усилие и условное напряжение. В точке R происходит разрыв образца по наименьшему сечению шей­ки (см. рис. 3.1, б).

Кроме перечисленных выше прочностных характеристик при ис­пытании на растяжение определяют характеристики пластичности материала, т.е. способности материала получать, не разрушаясь, боль­шие остаточные деформации. Это относительное остаточное удлине­ние при разрыве

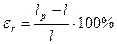
и относительное остаточное сужение при разрыве

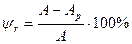
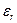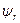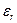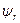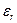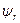Чем пластичнее материал, тем больше и . У пластичных ма­териалов (медь, алюминий, низкоуглеродистая сталь), = 30%, = 50%. Для хрупких материалов и находятся в пре­делах 2...5 %. Если испытываемый образец нагрузить, не доводя до разрушения, до состояния, соответствующего точке L диаграммы (см. рис. 3.1, в), а затем разгрузить, то процесс разгрузки изобразится прямой LL1. Эта прямая всегда параллельна участку ОА диаграммы. При разгрузке деформация полностью не исчезает. Она уменьшает­ся на величину упругой деформации, т.е. на величину отрезка L1M. Отрезок OL1 представляет собой остаточную (пластическую) дефор­мацию.

Противоположным свойству пластичности является хрупкость, т.е. способность материала разрушаться при незначительных оста­точных деформациях. Для хрупких материалов характерно разруше­ние при малых остаточных деформациях, поэтому при их испытании на растяжение определяется только предел прочности 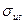. К хрупким материалам относят чугуны, высокоуглеродистые инстру­ментальные стали, стекло и др.

3.3 Твердость материалов

На производстве при необходимости быстрого контроля свойств изготавливаемых деталей, например контроля прочности после тер­мической или термохимической обработки, метод испытания образ­цов на растяжение имеет много неудобств. Применяют сравнитель­ную оценку свойств материала, минуя изготовление и разрушение образцов, путем измерения твердости.

Твердость (H) — способность материала оказывать сопротивле­ние проникновению в него другого, более твердого, тела. При вдавли­вании в материал инородного тела возникают местные пластические деформации, сопровождающиеся при дальнейшем увеличении на­грузки местным разрушением. Показатель твердости непосредствен­но связан с показателями прочности и пластичности. Твердость мате­риала тесно связана также с его обрабатываемостью: чем тверже материал, тем хуже он обрабатывается. От твердости зависит и изно­состойкость.

Испытания по определению твердости характеризуются быстро­той выполнения и не сопровождаются разрушением деталей. Сущест­вует несколько методов определения твердости. Выбор метода зависит от твердости испытуемого материала, толщины, размеров и формы изделия.

Метод Бринелля основан на вдавливании в поверхность ис­пытуемого материала стального закаленного шарика диаметром 2,5; 5 или 10 мм под действием силы F, приложенной перпендикулярно к поверхности изделия в течение определенного времени. Числом твердости по Бринеллю называется отношение нагрузки 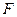к площади сферического отпечатка 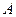, т.е. 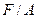. Твердость по Бринеллю при усло­виях испытания, когда диаметр шарика 10 мм, F— 3000 кгс и продол­жительность выдержки под нагрузкой от 10 до 15 с, обозначается цифрами, характеризующими число твердости, и буквами НВ (на­пример, 120 НВ, где 120 — число твердости, кгс/мм2; НВ — твердость по Бринеллю).

Методом Бринелля испытывают материалы с твердостью до 450 НВ, что связано с твердостью закаленных шариков. Этим методом нельзя определить твердость пленок, деталей после химико-термической об­работки из-за незначительной толщины обработанного поверхност­ного слоя.

По методу Роквелла о твердости судят по разности глубин, на которые проникает алмазный конус с углом при вершине 120° или стальной закаленный шарик диаметром 1,588 мм при действии двух последовательно приложенных нагрузок: предварительной, равной 10 кгс, и общей — 60, 100 или 150 кгс, равной сумме предварительной и основной нагрузок. Для определения числа твердости применяют три шкалы. Шкала В соответствует вдавливанию шарика, и число твердости при этом обозначается HRB. Для более твердых материалов применяются шкалы А и С, соответствующие вдавливанию алмазно­го конуса. Вначале индентор вдавливается в поверхность образца под предварительной нагрузкой, которая не снимается до конца испыта­ний, что обеспечивает точность измерений. Затем подается основная нагрузка (для шкалы А — 50 кгс, для шкалы В — 90 кгс, для шкалы С — 140 кгс), после снятия которой число твердости определяют глубиной отпечатка. Твердость по Роквеллу измеряется в условных единицах. За единицу твердости принята величина, соответствующая осевому перемещению индентора на 0,002 мм. По шкалам А, В и С устанавли­ваются следующие пределы измерения твердости: шкала А— 70...85 ед. (твердые сплавы, изделия с высокой поверхностной твердостью); шка­ла С — 20...67 ед. (термообработанная сталь); шкала В — 25...100 ед. (мягкие металлы и сплавы).

Твердость по Роквеллу обозначается цифрами, характеризующи­ми число твердости, и буквами HR с указанием шкалы (например, 60 HRC, где 60 — число твердости; HR — твердость по Роквеллу; С — шкала твердости).

Метод Роквелла получил широкое распространение благодаря высокой производительности (совмещение операций вдавливания индентора и измерения размеров отпечатка), универсальности, неболь­шому размеру отпечатка. В определенном интервале чисел твердости имеет место следующее отношение между твердостью по Бринеллю и Роквеллу: 1 HRC ≈ 10 НВ.

Метод Виккерса заключается во вдавливании в испытуемый материал правильной четырехгранной алмазной пирамиды с углом 136° между противоположными гранями. Число твердости по Виккерсу вычисляется путем деления нагрузки на площадь поверхности пи­рамидального отпечатка. Обычно используют таблицы, с помощью которых по длине диагонали отпечатка находят число твердости. Ес­ли при измерении твердости используется нагрузка F= 30 кгс и вре­мя выдержки 10...15 с, твердость обозначается буквами НV и цифра­ми, характеризующими число твердости (например, HV300, где HV— твердость по Виккерсу; 300 — число твердости, кгс/мм2).

Метод Виккерса широко применяется для определения твердо­сти тонких образцов и тонких поверхностных слоев металла после хи­мико-термической обработки, а также мелких деталей, деталей слож­ной формы.

Экспериментально установлено, что по значению твердости можно оценить предел прочности при растяжении 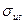, условный пре­дел текучести 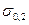, модуль упругости Е материала. Так, для конструк­ционных углеродистых сталей с НВ > 150 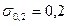НВ и 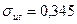НВ; для латуни 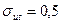НВ; для дюралюминия 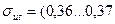) НВ и т.д.

Сдвиг и кручение

4.1. Напряжения и деформации при сдвиге

При простом растяжении две части стержня, разделенные на­клонным сечением, стремятся не только оторваться, но и сдвинуться относительно друг друга. Сдвигу противодействуют касательные на­пряжения в плоскости сечения.

На практике ряд деталей работает в таких условиях, при которых причиной разрушения является сдвиг одной части детали относи­тельно другой. При расчете на прочность таких деталей учитываются касательные напряжения, и расчет на прочность ведется по ним.

Пусть к стержню приложены перпендикулярно к его продольной оси две равные по модулю, но противоположно направленные силы, действующие очень близко друг от друга (рис. 4.1, а). При достаточ­ной величине этих сил произойдет срез — отделение правой части стержня от левой по сечению I—I. Деформации среза в зоне действия сил предшествует перекашивание прямых углов элементарного объе­ма — параллелепипеда с ребрами а, b,d и c (4.1, б). На гранях парал­лелепипеда возникают касательные напряжения, направление кото­рых определяется законом парности касательных напряжений. Если нормальные напряжения вызывают линейные деформации (удлине­ния и укорочения), то касательные напряжения вызывают угловые деформации γ — так называемые углы сдвига. При равенстве касатель­ных напряжений по площадкам элементов деформированного тела (закон парности касательных напряжений) имеем одинаковые угло­вые деформации, углы сдвига.

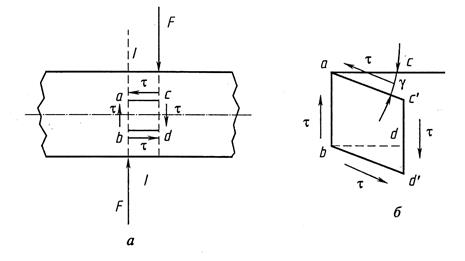
Рис. 4.1

Чистым сдвигом называют такое напряженное состояние, при
котором по граням элемента в виде бесконечно малого кубика дейст­
вуют только касательные напряжения. Например, чистый сдвиг на­блюдается во всех точках скручиваемого стержня с круглым поперечным сечением.

Пользуясь методом сечений, определим, что равнодействующая внутренних сил в плоскости 1-1(плоскости сдвига) (рис. 4.1, а) рав­на внешней силе 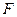, т.е. 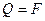. Эта сила может вызвать лишь касатель­ные напряжения, равномерно распределенные по плоскости сече­ния, поэтому

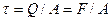
где 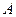- площадь поперечного сечения стержня.

Действительное распределение касательных напряжений по се­чению 1-1 не является равномерным; в узких краевых зонах касатель­ные напряжения приближаются к нулю. Но это обстоятельство при инженерных расчетах не принимается во внимание, так как область указанных отклонений мала по сравнению с размерами сечения.

Опыты показывают, что для большинства материалов до опреде­ленных величин нагружения имеется линейная зависимость между напряжениями и деформациями при сдвиге, которую выражает закон Гука:

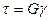
где 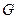— модуль упругости материала при сдвиге, или модуль упругости второго рода. Он связан с модулем упругости Е при растяжении через коэффициент Пуассона μ следующей зависимостью: 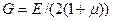. Отметим, что для стали 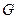≈ 8∙104 МПа, для алюминия 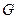≈ 2,7∙104 МПа.

Так как разрушение детали при деформации сдвига называют срезом, расчет на прочность при данной деформации называют расчетом на сдвиг или на срез. Примером соединений, рассчитываемых на срез, являются заклепочные, болтовые, сварные, паяные, клеевые со­единения.

Условие прочности при сдвиге имеет вид:

,

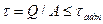где 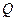— равнодействующая внутренних сил в плоскости сдвига; 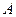— площадь сдвига; 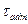— допускаемое касательное напряжение мате­риала детали.

4.2 Статические моменты сечения. Центр масс сечения

При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций за­висит только от площади поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при расчетах сжатых стержней на устойчивость, прочность и жесткость элементов конст­рукции зависят также от формы их поперечного сечения. К числу геометрических характеристик сечения, учитывающих его размеры, форму и влияющих на прочность и жесткость конструкций, относят­ся статические моменты, моменты инерции и моменты сопротивле­ния сечения.

Статическим моментом сечения S относительно любой оси на­зывается взятая по всей площади сечения сумма произведений пло­щадей п элементарных площадок и их расстояний до этой оси. Так, статический момент сечения (рис. 4.2) относительно оси OZ

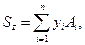
где n — число элементарных площадок сечения; Ai — площадь эле­ментарной i-й площадки сечения, расположенной на расстоянии yi , от оси OZ.

При 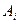→ 0 и n → ∞

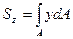
где 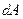— элементарная площадка.

Размерность статических моментов — длина в кубе. Статические моменты могут быть положительными, отрицательными и равными нулю.

Считая, что поверхностная плотность 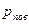сечения постоянна, координаты центра масс сечения 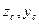, можно выразить через стати­ческие моменты:

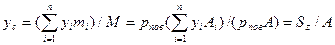
Аналогично

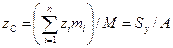
где 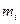— массы элементарных площадок сечения; М — масса сечения; А — площадь сечения; 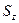, 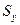—статические моменты сечения относи­тельно координатных осей OZ и OY соответственно.

Из приведенных выражений видно, что при 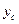=0, 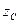=0, т.е. при прохождении координатных осей через центр масс С, статические мо­менты сечения относительно этих осей будут равны нулю, так как 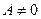. Такие координатные оси называют центральными. Это следст­вие можно выразить еще так: если статические моменты сечения от­носительно координатных осей, например OZ и OY, равны нулю, т.е. 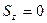, , 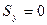то эти оси проходят через центр масс С сечения.

4.3 Моменты инерции сечений

Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных пло­щадок и квадратов расстояний от них до данного полюса (точки). Из рис. 4.2 находим:

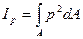
где 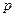— расстояние от площадки 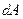до полюса (точки О),

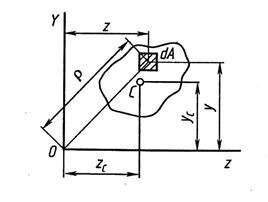
Рис. 4.2

Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных пло­щадок и квадратов расстояний от них до оси. Так, моменты инерции сечения относительно координатных осей OZ и OY Отбудут соответст­венно равны:

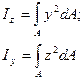
Так как 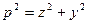, то, сравнив приведенные выражения, по­лучим

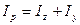
т.е. сумма осевых моментов инерции сечения относительно двух вза­имно перпендикулярных осей равна полярному моменту инерции это­го сечения относительно точки пересечения рассматриваемых осей. Моменты инерции сечений — всегда положительные величины.

4.4 Понятие о крутящем моменте

Деформация кручения происходит при действии на стержень пар внешних сил, плоскости действия которых перпендикулярны к оси стержня. При этом в поперечных сечениях стержня возникает только одна составляющая внутренних сил — крутящий момент 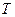. С явлени­ем кручения встречаются при расчете валов, винтовых пружин и дру­гих элементов конструкций.

Если прямые незакрепленные стержни, подвергающиеся дефор­мации кручения, равномерно вращаются или находятся в покое, ал­гебраическая сумма всех внешних скручивающих (вращающих) мо­ментов 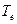равна нулю.

Вращающиеся и испытывающие деформацию кручения стержни называют валами. При расчете валов величины скручивающих мо­ментов можно определить по передаваемой мощности и скорости вращения вала по выражению:

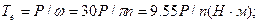
где 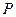— мощность, передаваемая валом, Вт; 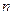— частота вращения вала, об/мин; 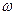— угловая скорость, рад/с.

С помощью метода сечений устанавливаем, что крутящий мо­мент 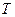в произвольном поперечном сечении стержня численно равен алгебраической сумме внешних скручивающих моментов 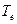, дейст­вующих на стержень по одну сторону от рассматриваемого сечения. Когда к валу приложено несколько внешних скручивающих момен­тов 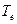, крутящие моменты в сечениях различных участков будут раз­ными. Для наглядности распределения 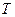по длине скручиваемого стержня и для нахождения опасного сечения с наибольшим крутя­щим моментом 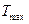строят эпюры (графики) крутящих моментов (рис. 4.3).

При построении эпюры Т проводят ось, параллельную оси стержня. Каждая ордината эпюры в принятом масштабе равна крутя­щему моменту, действующему в том сечении, которому соответствует ордината. При расчетах на прочность и жесткость знак 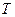не играет роли, но для удобства построения эпюр будем считать крутящий мо­мент 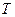положительным, если при взгляде в торец отсеченной части стержня этот момент представляется направленным против хода ча­совой стрелки. Положительные по знаку крутящие моменты откла­дывают на эпюре выше оси, отрицательные — ниже.

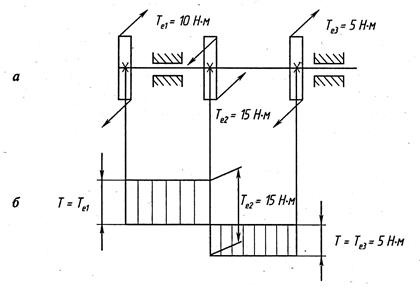
Рис. 4.3

На рис. 4.3, б представлена эпюра крутящих моментов Т для схе­мы нагружения вала тремя внешними моментами 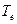(рис. 4.3, а). От­метим, что в сечениях, в которых приложен внешний скручивающий момент Те , ордината эпюры Т меняется скачком на величину, равную значению этого момента. Как видно из рис. 4.3, б, максимальный крутящий момент ( 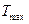= 10 Н·м) не всегда равен наибольшему мо­менту внешних сил ( 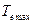= 15 Н·м).

4.5 Определение напряжений при кручении стержней с круглым поперечным сечением

Рассмотрим стержень с круглым поперечным сечением (рис. 4.4, а), один конец которого закреплен, а другой нагружен парой сил с мо­ментом 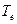. В результате действия момента внешних сил 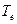возникает деформация кручения. Наблюдая при кручении особенности искаже­ния прямоугольников координатной сетки, нанесенной на боковой поверхности круглого стержня, обнаружили следующее: прямоугольная сетка превратилась в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных, а с учетом закона парности касательных напряжений — и в продоль­ных сечениях. Контуры поперечных сечений в процессе деформации остались плоскими, расстояния между ними не изменились, а первона­чальные прямолинейные образующие, нанесенные на боковую поверх­ность, превратились в винтовые линии; диаметры торцового сечения повернулись на некоторый угол 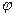относительно своего начального положения, оставаясь прямой линией. Эти наблюдения позволили составить представление о механизме деформации кручения. Посто­янство длины и диаметра деформируемого стержня свидетельствует об отсутствии нормальных напряжений в поперечных и продольных сечениях. Так как в поперечных и продольных сечениях действуют только касательные напряжения, напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг. Попереч­ные сечения, оставаясь плоскими, поворачиваются вокруг оси стерж­ня относительно друг друга на некоторый угол, сохраняя длину и пря­молинейность своих радиусов.

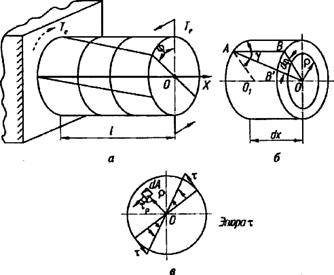
Рис. 4.4

Выделим двумя поперечными сечениями элемент скручиваемого стержня длиной 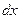(рис. 4.4, б). В результате деформации одно сече­ние повернется относительно другого на угол 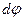. Будем считать левое сечение элемента 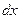неподвижно закрепленным. Тогда 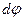— угол по­ворота правого торцового сечения вокруг продольной оси. Обра­зующую АВОО 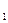можно представить как параллелепипед длиной 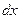с бесконечно малыми основаниями АО 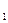и ВО. В результате деформа­ции этот параллелепипед займет положение AВ'ОО 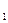. Величина BB'= 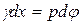представляет собой абсолютный сдвиг грани В на по­верхности стержня относительно грани А в направлении, перпенди­кулярном к радиусу стержня. Величина абсолютного сдвига точек ос­нования ВО параллелепипеда зависит от их расстояния ρ до оси стержня. Сдвиг равен нулю на оси стержня и максимален, т.е. равен ВВ', на поверхности. Угол сдвига

,

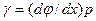где 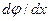— относительный угол закручивания.

На основании закона Гука для сдвига можно записать:

,

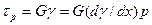где 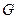— модуль упругости материала стержня при сдвиге.

Как видно из последнего выражения, касательные напряжения в каж­дой точке сечения прямо пропорциональны расстоянию ρ от точки до центра масс сечения. На оси стержня при 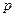= 0 напряжение 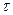= 0; в точках, расположенных в непосредственной близости от поверхно­сти стержня, напряжения максимальны. Эпюра изменения 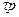вдоль диаметра сечения показана на рис. 4.4, е. Так как величина относи­тельного угла закручивания 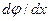неизвестна, последней зависимостью для определения касательных напряжений в сечении не пользуются.

Действующая в плоскости сечения на площадку 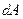с напряжени­ем 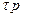элементарная внутренняя сила 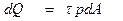. Элементарный мо­мент внутренних сил, действующий в плоскости сечения, т.е. элемен­тарный крутящий момент, создаваемый силой 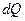относительно центра сечения, 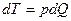. Сумма этих моментов внутренних сил по всей пло­щади поперечного сечения стержня равна крутящему моменту

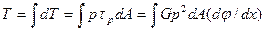
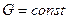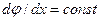Так как и , то

,

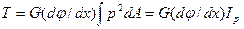где 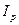— полярный момент инерции сечения.

Выразим из последнего равенства величину угла закручивания, отне­сенного к единице длины стержня:

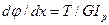
Выражение для 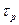с учетом последней формулы примет вид

.

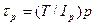При инженерных расчетах интерес представляют наибольшие напряжения в сечении, т.е. напряжения на поверхности стержня при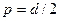

,

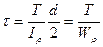где 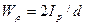— полярный момент сопротивления (отношение по­лярного момента инерции 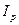сечения к расстоянию от наиболее уда­ленной точки сечения до центра масс).

Полярный момент сопротив­ления для стержня круглого сечения диаметром 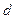равен 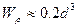, а для стержня кольцевого сечения с внутренним диаметром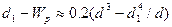

Условие прочности стержня при кручении с постоянным по дли­не поперечным сечением имеет вид

,

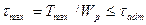где 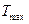— максимальный крутящий момент по длине деформируемо­го стержня; τadm — допускаемое напряжение при кручении; для стали оно обычно равно 0,5...0,6 допускаемого напряжения 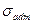при растя­жении. Предельный из условия прочности крутящий момент опреде­ляют по формуле:

,

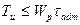а минимальный диаметр скручиваемого стержня (учитывая, что

)

.

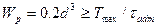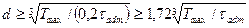При сравнении стержней, выдерживающих одинаковый крутя­щий момент, т.е. имеющих поперечное сечение с равным полярным моментом сопротивления 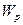, стержень с наименьшей площадью A поперечного сечения будет обладать меньшей массой. Для сравнения различных сечений применяют безразмерную величину, равную от­ношению 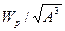. Чем больше эта величина, тем рациональнее по затратам материала сечение. Так, для швеллера, двутавра она равна 0,04...0,07, а для круглого кольца с отношением внутреннего диаметра к внешнему 0,9 она равна 1,16. При кручении рационально использо­вать стержни с круглым кольцеобразным сечением.

4.6 Определение деформаций при кручении стержней с круглым поперечным сечением

Деформация при кручении стержней определяется углом пово­рота поперечных сечений относительно начального положения. Вос­пользуемся формулой для выражения угла поворота сечения скручиваемого стержня на участке длиной :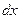

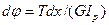
На участке длиной l полный угол закручивания

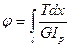
Если крутящий момент Т и величина 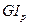, называемая жесткостью при кручении, постоянны на всей длине l, то полный угол закру­чивания φ (в радианах)

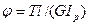
Расчет стержней на прочность при кручении не исключает воз­можности возникновения недопустимых деформаций (углов пово­рота поперечных сечений) при целостности длинных стержней (де­талей). Поэтому часто детали, испытывающие деформацию круче­ния, рассчитывают не только на прочность, но и на жесткость. Для обеспечения требуемой жесткости необходи