Машины и механизмы, их структура и классификация

Для облегчения труда человека, повышения производительности используют машины — устройства для обработки, преобразования материалов, энергии и информации с помощью определенных целе­сообразных механических движений. В технологических машинах изменяются размеры, форма и состояние (твердое, жидкое и др.) об­рабатываемых объектов. В транспортных машинах происходит пере­мещение различных объектов с требуемой скоростью, в энергетиче­ских и информационных машинах — преобразование соответственно энергии или вводимой информации для контроля, регулирования и управления движением.

Машина выполняет свои функции с помощью определенных механических движений, носителем которых является механизм. Ме­ханизмом называют искусственно созданную систему подвижно со­единенных тел (звеньев), предназначенную для преобразования заданного движения одного или нескольких из них в требуемое дви­жение остальных. Машина состоит из сочетания механизмов.

1.1 Звенья и кинематические пары механизмов

Подвижно соединенные между собой части механизма называют звеньями. Звеном может быть одна или несколько неподвижно соеди­ненных между собой деталей.

В состав любого механизма входят как неподвижное звено (стой­ка), так и подвижные звенья. К стойке относят элементы неподвиж­ной системы механизма, например корпус и детали, жестко связан­ные с ним. Подвижное звено независимо от количества входящих в него деталей образует жесткую систему, для которой характерен одинаковый вид движения.

В механизме различают ведущие звенья, которые получают движе­ние от внешних источников энергии, и ведомые — все остальные под­вижные звенья, получающие определенное движение от ведущих звеньев. Закон движения ведущих звеньев обычно задан. Движение ведомых звеньев исследуется по отношению к неподвижной системе жестко связанных тел — к стойке. В принтере, например, к стойке следует отнести корпус печатающего устройства, все детали и платы, жестко связанные с ним. Ведомое звено, совершающее требуемое движение, которое получают с помощью механизма, называют рабочим.

Звенья механизмов могут обладать различными физическими свойствами. Наряду с абсолютно твердыми звеньями в механизмах используются упругие и гибкие звенья, характеризующиеся возмож­ностью изменения своей формы, размеров. В качестве упругих звень­ев применяют различного вида пружины, мембраны, металлорезиновые соединения. К гибким звеньям относятся ремни, ленты, пассики, нерастяжимые нити и т.д.

При изучении движения механизма звенья изображают упрощен­но, без учета многих особенностей конструкции (ГОСТ 2.770—74). Так, на рис. 1.1, а изображены звенья типа вала, стержня, ползуна. Для указания неподвижности любого звена часть его контура покрывают штриховкой (рис. 1.1,6). Неподвижное соединение частей звена и не­подвижное соединение детали с валом показаны на рис. 1.1, в и г соот­ветственно.

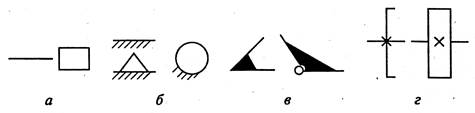
Рис. 1.1

Основными признаками механизма являются подвижность звеньев и определенность в преобразовании их движений. Подвижные звенья входят в соединение друг с другом или с не­подвижным звеном так, что имеется возможность движения одного звена относительно другого. Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кине­матической парой.

Поверхности, линии, точки, по которым одно звено соприкасается с другим, образуя кинематическую пару, называют элементами пары.

Кинематические пары налагают на относительные движения звеньев ограничения, зависящие от способа соединения звеньев пары. Из­вестно, что всякое свободное твердое тело имеет шесть степеней сво­боды, которые можно представить в виде простейших движений: три вращения вокруг координатных осей и три поступательных переме­щения вдоль этих осей (рис. 1.2, а). Присоединением звеньев меха­низма друг к другу ограничиваются некоторые из указанных движе­ний. Ограничения, налагаемые на относительные движения звеньев 1 и 2, входящих в кинематическую пару (рис. 1.2, б, г—е), называются условиями связи. Очевидно, что число ограничений может быть только целым и должно быть меньше шести, так как в противном случае зве­нья теряют относительную подвижность и кинематическая пара пере­ходит в неподвижное соединение звеньев. Число условий связи не может быть меньше единицы, иначе звенья не соприкасаются и кине­матическая пара перестает существовать.

Для удобства анализа структуры механизмов кинематические пары классифицируют по различным признакам.

В зависимости от числа отнятых кинематической парой независимых возможных перемещений звеньев, т.е. от числа отнятых степеней свободы, пары делятся на пять классов; порядок класса соответствует числу ограничений дви­жения. На рис. 1.2, б, в показаны пары соответственно 3-го и 4-го классов, на рис. 1.2, г—е — пары 5-го класса (поступательная, враща­тельная, винтовая). Кинематические пары 5-го класса имеют наи­большее распространение, поскольку являются основой направляю­щих поступательного и вращательного движений.

По характеру относительного движения звеньев кинематические пары делят на плоские и пространственные. Точки звеньев, входящих в плоские пары, могут двигаться в одной или парал­лельных плоскостях. К плоским кинематическим парам относятся пары только 5-го и 4-го классов, так как свободное тело, совершаю­щее плоское движение, имеет только три степени свободы, три возможных простейших движения: два поступательных вдоль коорди­натных осей плоскости и вращательное в плоскости движения. Точки звеньев пространственных пар при движении описывают пространст­венные кривые.

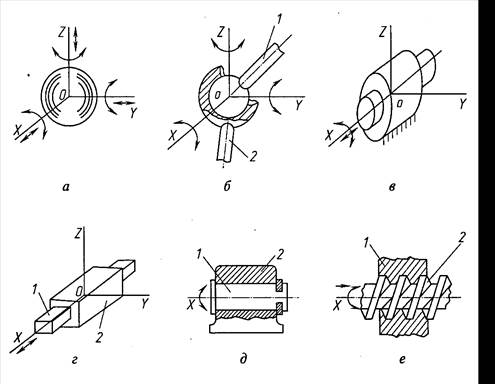
Рис. 1.2

По характеру соприкосновения звеньев в кинемати­ческой паре последние делят на низшие и высшие. Низшими называ­ют такие пары, в которых соприкосновение звеньев происходит по поверхности (рис. 1.3). В высших кинематических парах соприкоснове­ние звеньев происходит по линии или в точке. Преимущество высших пар - возможность воспроизводить достаточно сложные относитель­ные движения, меньшие потери на трение. Достоинством низших пар является способность их элементов воспринимать и передавать зна­чительные нагрузки при меньшем износе. Высшие пары образуются боковыми поверхностями зубьев колес, находящихся в зацеплении, роликами фрикционных передач, кулачком и толкателем. В плоских механизмах высшая пара относится к 4-му классу, ее называют парой качения со скольжением.

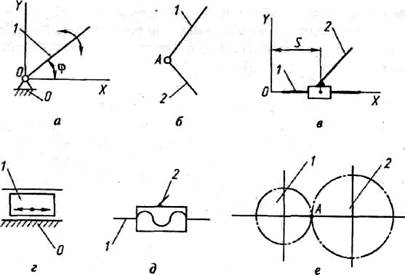
Рис. 1.3

По способам замыкания, т.е. обеспечения постоянного соприкосновения элементов, кинематические пары классифицируют на геометрически незамкнутые (силовые) и замкнутые. В первых пара существует за счет прижатия одного звена к другому силами тяжести, упругости пружин, электромагнитного притяжения, во вторых со­прикосновение звеньев обеспечивается геометрическими формами элементов (см. рис. 1.2, б - е).

1.2 Кинематические цепи. Степень подвижности механизмов

При изучении движения механизма все звенья и кинематические пары изображают на схемах упрощенно. Условные изображения наиболее часто используемых кинематиче­ских пар 5-го и 4-го классов показаны на рис. 1.3: д, б – вращательные пары с подвижными 1, 2 и неподвижным 0 звеньями; в, г — поступа­тельная; д — винтовая; е — пара 4-го класса в месте зацепления А зуб­чатых колес 1 и 2.

Звенья соединяются с помощью кинематических пар в кинема­тические цепи. В зависимости от характера движения звеньев различают плоские и пространственные кинематические цепи. Плоские цепи образуются звеньями, совершающими плоское движение; точки звеньев пространственных цепей описывают про­странственные траектории.

Кинематические цепи делятся на простые и сложные. В простой цепи каждое звено входит не более чем в две кинематические пары (рис. 1.4, а). Различают незамкнутые (открытые) и замкнутые кине­матические цепи. В незамкнутой кинематической цепи есть звенья, входящие только в одну кинематическую пару (рис. 1.4, б); в замкну­той цепивсе звенья входят не менее чем в две кинематические пары.

Механизм можно представить в виде кинематической цепи, обя­зательно имеющей одно неподвижное звено — стойку. Но не любая кинематическая цепь может быть механизмом. Известно, что важ­нейшим свойством любого механизма является его подвижность, ко­торая оценивается степенью подвижности (свободы) механизма. Она равна числу независимых движений, которые нужно задать ведущему (ведущим) звену механизма, чтобы получить вполне определенное движение всех остальных подвижных звеньев. Степень подвижности механизма должна быть не менее единицы и равна числу независимых кинематических параметров (перемещений). В плоских механизмах ведущие звенья совершают обычно одно простое движение — вращательное или по­ступательное, поэтому для таких механизмов степень подвижности равна числу ведущих звеньев. Может быть одно или несколько веду­щих звеньев. Если ведущее звено совершает вращение вокруг непо­движной оси, его положение определяется углом поворота звена. Если же ведущее звено совершает поступатель­ное движение, его положение определяется координатой линейного перемещения звена.

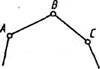
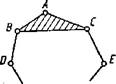
а б

Рис. 1.4

Степень подвижности механизма можно определить из его струк­турной формулы, связывающей подвижность с числом звеньев, числом и классом кинематических пар. Пусть механизм состоит из к звеньев. Так как одно из звеньев (стойка) является неподвижным, количество подвижных звеньев механизма п = к -1.

Рассмотрим пространственный механизм. Если бы звенья меха­низма не были связаны кинематическими парами, то общее количе­ство простейших движений всех его подвижных звеньев равнялось бы 6п. Пусть в механизм входит: р_х пар 1-го класса; р₂ пар 2-го класса; р₃ пар 3-го класса; р₄ пар 4-го класса и р₅ пар 5-го класса. Каждая кине­матическая пара 1-го класса ограничивает одно простейшее движение, а все пары 1-го класса делают невозможными р_х движений. Каждая пара 2-го класса ограничивает два простейших движения, а все пары 2-го класса — 2р₂ движений. Аналогично рассуждая, видим, что ки­нематические пары 3, 4 и 5-го классов исключают соответственно 3p₃ ,4р₄ и 5р₅ простейших движений подвижных звеньев механизма. Число независимых возможных движений пространственного меха­низма, состоящего из п подвижных звеньев,

W=6n - 1p₁ - 2р₂ – 3p₃ -4р₄ - 5р₅. (1.1)

Определим степень подвижности плоских механизмов (как наи­более распространенных). В плоском движении подвижные звенья, не связанные кинематическими парами, имели бы 3п степеней свобо­ды (подвижности). Каждая кинематическая пара 5-го класса отнима­ет у звена два простейших движения, а каждая кинематическая пара 4-го класса — одно. Следовательно, кинематические пары 5-го класса отнимают у плоской кинематической цепи 2р₅, а 4-го класса — 1р₄ степеней свободы. Степень подвижности плоского механизма в этом случае определяется по формуле

W=3n - 2p₅ - p₄. (1.2)

Зависимости (1.1) и (1.2) по имени их авторов называют формула­ми Малышева и Чебышева соответственно. Они помогают оценить, можно ли использовать ту или иную кинематическую цепь в качестве структурной схемы механизма, а также число ведущих звеньев меха­низма. Так, для схем, приведенных на рис. 1.5, а—в, степень подвиж­ности равна соответственно 0, 1 и 2. Кинематическая цепь, представ­ленная на рис. 1.5, а, не может использоваться для преобразования движения, а число ведущих звеньев механизмов, приведенных на рис. 1.5, б, в, должно быть равно соответственно 1 и 2.

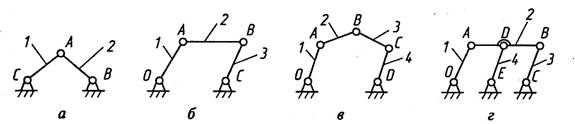
Рис. 1.5

Преимущественное распространение получили механизмы с од­ной или двумя степенями подвижности. Встречаются механизмы, число степеней подвижности которых не соответствует условию (1.2). В общее число наложенных ограничений может войти некоторое чис­ло повторных (лишних) связей, введенных в механизм по различным причинам. В механизме шарнирного параллелограмма (рис. 1.5, б), имеющего W = 1, для увеличения жесткости к звену 2 и стойке при­соединили дополнительно звено 4 (рис. 1.5, г). Это звено и кинемати­ческие пары D и Е вдействительности не изменили кинематики меха­низма, но, согласно формуле (1.2), «уменьшили» степень подвижности до нуля. Связи, не влияющие на кинематику механизма, а формально уменьшающие степень его подвижности, называют пассивными. В неко­торых механизмах есть звенья, относительные движения которых не влияют на кинематику механизма. Такие механизмы имеют «лиш­ние» степени свободы. Например, вращение круглого ролика на кон­це ведомого звена кулачкового механизма не влияет ни на движения кулачка, ни на движение этого звена, но формально создает лишнюю степень свободы.

1.3 Классификация механизмов

Механизмы, входящие в состав любой машины или прибора, весьма разнообразны. По функциональному назначению они делятся на следующие виды: механизмы двигателей и преобразо­вателей; передаточные механизмы; исполнительные механизмы; ме­ханизмы настройки, подачи, транспортирования; механизмы управ­ления, контроля и регулирования.

Механизмы решают задачи преобразования одних видов движений в другие, например вращательного в поступательное, и задачи изме­нения скорости при сохранении вида движения, например уменьше­ние числа оборотов двигателя до числа оборотов основного ведомого (рабочего) звена. В последнем случае одним из основных параметров механизма является передаточное отношение i, которое определяется как отношение угловых скоростей ведущего и ведомого звеньев механизма. Если механизм служит для понижения угловой скоро­сти, его называют редуктором, если для повышения, — мультипли­катором.

Механизмы, служащие для передачи вращательного движения с преобразованием скорости (фрикционные, зубчатые), называют передачами.

В зависимости от конструктивных особенностей и способа передачи движения между подвижными звенья­ми механизмы делят на шарнирно-рычажные, фрикционные, зубча­тые, кулачковые, винтовые, с гибкими звеньями. Рассмотрим под­робнее механизмы названных видов, учитывая их кинематические свойства и конструктивные особенности.

В шарнирно-рычажных механизмах жесткие звенья типа стержней, рычагов соединяются вращательными и поступательными кинемати­ческими парами. Шарнирно-рычажные механизмы применяются для преобразования вращательного или поступательного движения в лю­бое движение с требуемыми параметрами. Наибольшее распростра­нение получили плоские четырехзвенные механизмы с тремя по­движными и одним неподвижным звеньями. «Родоначальником» этой группы является шарнирный четырехзвенник (рис. 1.6), служа­щий для преобразования равномерного вращения ведущего звена 1 в неравномерное вращение звена 3. Звенья 1 и 3 называются кривоши­пами, если они поворачиваются на угол более 2π, и коромыслами, если совершают качательное движение. Звено 2, совершающее плоское движение, называют шатуном. В зависимости от соотношения длин звеньев механизма рабочее звено 3 может быть кривошипом или ко­ромыслом.

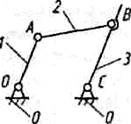
Рис. 1.6

Фрикционные механизмы используются в приводах систем, устрой­ствах транспортирования различных носителей информации. Передача движения в них осуществляется за счет сил трения между звеньями.

Фрикционные механизмы разнообразны по конструкции. Разли­чают фрикционные передачи с постоянным (рис. 1.7, а, б) и перемен­ным передаточным отношением (вариаторы) (рис. 1.7, в), твердыми (жесткими) звеньями и гибкой связью (рис. 1.7, г).

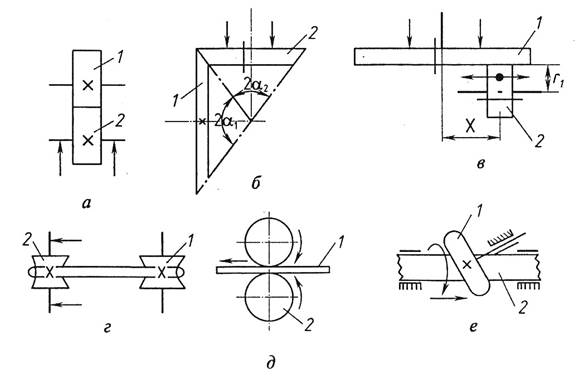
Рис. 1.7

По относительному расположению осей звеньев различают пере­дачи с параллельными (рис. 1.7, а) и пересекающимися (рис. 1.7, б) осями. Фрикционные передачи служат для преобразования вращательного движения ведущего звена во вращательное с другой скоро­стью (рис. 1.7, а - в), прямолинейное (рис. 1.7, д) или винтовое движение ведомого звена (рис. 1.7, е).

Кроме бесступенчатого изменения скорости ведомого звена к достоинствам фрикционных механизмов относятся простота конст­рукции, автоматическое предохранение от поломок при перегрузках, плавность передачи движения. К недостаткам рассматриваемых ме­ханизмов следует отнести непостоянство передаточного отношения из-за проскальзывания, наличие усилия, сжимающего катки, и уси­ленный в связи с этим износ звеньев.

Зубчатые механизмы получили наибольшее распространение благодаря ряду достоинств — компактности, высокому КПД, надеж­ности работы, простоте ухода, возможности применения в широком диапазоне скоростей и передаточных отношений, сохранению с боль­шой точностью заданного передаточного отношения. Передача дви­жения в них осуществляется зацеплением зубьев подвижных звень­ев — зубчатых колес. Недостатки зубчатых механизмов — сложность и высокая точность изготовления и сборки звеньев, шум при больших окружных скоростях колес.

Зубчатые передачи служат для изменения скорости вращательного движения (рис. 1.8, а—д), преобразования возвратно-вращательного движения в возвратно-поступательное, и наоборот (рис. 1.8, е).

Простейший одноступенчатый зубчатый механизм состоит из стойки и двух подвижных звеньев — зубчатых колес. Колеса образуют со стойкой вращательные пары 5-го класса, а друг с другом — высшую кинематическую пару 4-го класса, называемую зубчатым зацеплением.

По характеру относительного расположения осей вращения зубчатых колес различают передачи с параллельны­ми (рис. 1.8, а), пересекающимися (рис. 1.8, б) и перекрещивающи­мися в пространстве осями (рис. 1.8, в).

По виду зацепления или характеру расположения зубьев на теле зубчатых колес различают передачи с внешним (рис. 1.8, а) и внутренним (рис. 1.8, д) зацеплением. При внешнем зацеплении колеса с параллельными осями вращаются в разные сто­роны, при внутреннем — в одну.

Зубчатые передачи могут быть с постоянным и переменным пе­редаточным отношением. Применяют их для понижения и повыше­ния угловой скорости. В зависимости от назначения передачи и спе­цифических требований (износостойкость, бесшумность) зубья колес могут быть прямыми, косыми, шевронными и криволинейными. Зубчатые механизмы можно классифицировать еще по числу под­вижных звеньев, профилю боковых поверхностей зубьев и другим признакам. По профилю зуба различают эвольвентные, циклоидные, часовые, цевочные передачи, передачи Новикова и др. Наиболее ши­рокое применение получили эвольвентные передачи благодаря про­стоте технологии изготовления, большой кинематической точности, малой чувствительности к изменению межосевого расстояния.

В особую группу зубчатых передач можно выделить эпицикличе­ские передачи, основным признаком которых является наличие колес с подвижными геометрическими осями (рис. 1.8, г). Колеса 1, 3, имеющие неподвижные геометрические оси, называют центральны­ми, колесо 2 сподвижной геометрической осью — сателлитом; звено Н, вращающее оси сателлитов, — водилом. Эпициклические переда­чи, имеющие одну степень подвижности, называются планетарными, а две — дифференциальными. Рассматриваемые передачи позволяют «снимать» с одного вала движения с различными скоростями, что ши­роко используется в шкальных механизмах. Эпициклические переда­чи при малых габаритах позволяют получать большие передаточные отношения.

Кулачковые механизмышироко применяются в устройствах управления, прерывистого движения. Простейший кулачковый меха­низм (рис. 1.9, а) состоит из кулачка 1, толкателя 2, стойки и образует в точке А высшую кинематическую пару 4-го класса. Ведущее звено 1 называется кулачком или эксцентриком. Форма профиля кулачка определяется законом движения толкателя и может быть самой раз­нообразной, как и закон движения ведомого звена. Кулачковые меха­низмы позволяют получать любой закон движения ведомого звена, отличаются простотой, компактностью, малыми габаритами.

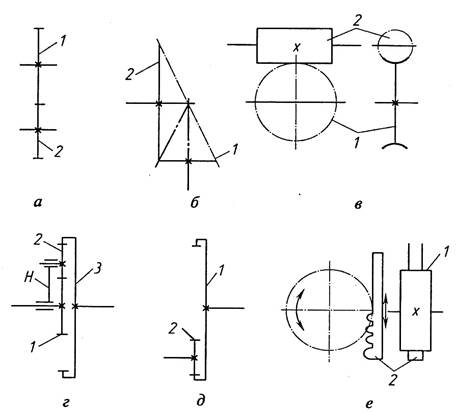
Рис. 1.8

К недостаткам кулачковых механизмов следует отнести боль­шие удельные давления в высшей паре и, следовательно, недолговеч­ность механизма, а

также необходимость в силовом замыкании звень­ев. Возможно геометрическое замыкание с помощью пазов в кулачке, который направляет движение ведомого звена.

Величина перемещений и закон движения рабочего звена меха­низма определяются профилем кулачка.

По виду преобразуемых движений кулачковые меха­низмы можно разделить на следующие группы: механизмы, в которых вращательное движение кулачка 1 преобразуется в возвратно-поступа­тельное или качательное движение толкателя 2 (рис. 1.9, а и б соответ­ственно); механизмы, в которых возвратно-поступательное движение кулачка 1 преобразуется в возвратно-поступательное или качательное движение толкателя 2 (рис. 1.9, виг соответственно); пространст­венные, или коноидные, кулачковые механизмы, решающие функ­ции двух переменных, например 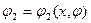(рис. 1.9, д). Эти меха­низмы имеют две степени свободы. Применяются они в передающих устройствах.

Толкатели кулачковых механизмов в зависимости от вида кинема­тического элемента толкателя подразделяются на точечные (рис. 1.9, д), плоские и тарельчатые (рис. 1.9, а), с профилем, очерченным по радиу­су или сфере, роликовые и шариковые (рис. 1.9, в и г соответственно).

Винтовые механизмысостоят из винта и гайки и предназначены для преобразования вращательного движения в прямолинейное, и наобо­рот. Они обеспечивают высокую точность поступательных перемеще­ний, большой выигрыш в силе. Недостатки — большие потери на трение в паре винт — гайка, низкий КПД. Применяются винтовые механизмы в измерительных приборах, механизмах точных перемещений, регули­рования и настройки, в подъемно-транспортных устройствах.

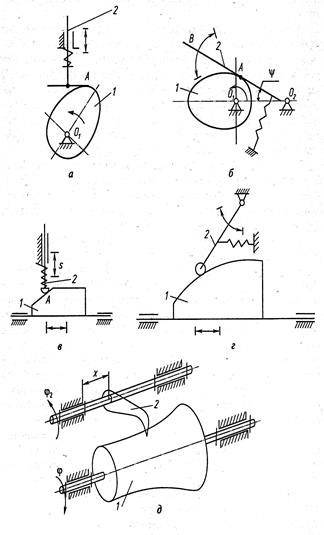
Рис. 1.9

При вращении винта 1 (рис. 1.10) гайка 2 поступательно переме­щается в направляющих стойки 3. Возможно использование схемы, в которой ведущим звеном является зафиксированная в осевом на­правлении вращающаяся гайка, а ведомым — винт, движущийся по­ступательно в направляющих стойки.

Имеются конструкции кинематической пары винт — гайка с тре­нием скольжения и трением качения.

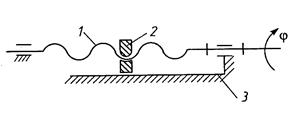
Рис. 1.10

Механизмы с гибкими звеньямиприменяют для передачи враща­тельного движения между валами при больших межосевых расстоя­ниях и для преобразования вращательного движения в поступатель­ное, и наоборот. Ведущее и ведомое жесткие звенья таких механизмов непосредственно не контактируют друг с другом, а передача движе­ния осуществляется посредством гибкого звена, которое может быть как замкнутым, так и разомкнутым.

По характеру соединения гибкого звена с ведущим и ведомым звеньями рассматриваемые механизмы подразделяют на передачи трением, передачи зацепления ипередачи с жестким креплением гибкого звена к другим звеньям.

В передачах трениемв качестве гибкого звена используют пло­ские и клиновидные ремни, пассики, круглые шнуры и ремни, нити (рис. 1.11, а). Передача состоит из ведущего 1 и ведомого 2 шкивов, а также замкнутого звена 3, надетого на шкивы с натяжением. Таким передачам присущи все достоинства и недостатки фрикционных ме­ханизмов непосредственного касания. Необходимым условием нор­мальной работы передачи трением является натяжение гибкого зве­на, что достигается обычно с помощью натяжного ролика 4.

В передачах зацепления гибким звеном служит зубчатый ремень, перфорированная лента, цепь (рис. 1.11, б). Преимущества этих пере­дач перед передачами трением соответствуют преимуществам зубча­тых передач по отношению к фрикционным.

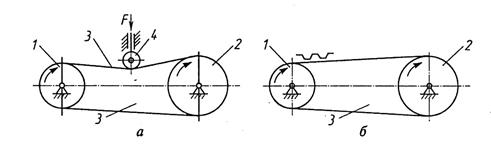
Рис. 1.11