Основы расчетов деталей механизмов и машин на прочность

2.1 Деформации и напряжения. Метод сечений

Любой механизм или машина помимо других свойств должен обладать проч­ностью, т.е. способностью его деталей, соединений выдерживать, не разрушаясь, действие внешних сил (нагрузок).

Способность элемента конструкции сопротивляться изменению своих первона­чальных размеров и формы называется жесткостью.

Помимо расчетов на прочность и жесткость в ряде задач серьез­ное внимание уделяется вопросам устойчивости. Под устойчивостью понимают способность звена сохранять определенную начальную форму равновесия. Равновесие устойчиво, если малому изменению нагрузки соответствует малое изменение деформаций. И, естествен­но, равновесие неустойчиво, если ограниченный рост нагрузки со­провождается неограниченным ростом деформаций.

Деформация — это изменение формы и размеров тел (звеньев ме­ханизма) под действием внешних сил. Деформация, исчезающая по­сле снятия вызвавших ее нагрузок, называется упругой, а свойство тела восстанавливать свои первоначальные размеры — упругостью. Если деформация после снятия нагрузки не исчезает, она называется остаточной. Остаточная деформация, не сопровождающаяся разру­шением, называется пластической, а остаточная деформация, завися­щая от времени деформирования, — вязкой.

Смещение частиц материала детали при деформации сопровож­дается изменением сил их взаимодействия (притяжения и отталкивания). Возникают внутренние силы — силы противодействия деформации (силы упругости). Интенсивность внутренних сил характеризуется напряжением. Напряжение связывают не только с точкой тела, но и с сечением, проходящим через данную точку. В одной и той же точ­ке напряжение в разных сечениях, проходящих через нее, может быть различным.

Напряжением в точке называют внутреннюю силу, кото­рая приходится на единицу площади, выделенную у точки по прове­денному сечению. При определении напряжений нужно прежде всего уметь вычислять внутренние силы в требуемых сечениях, естествен­но, через известные величины, т.е. через внешние силы, действую­щие на тело.

Внутренние силы определяют с помощью метода сечений. Согласно этому методу, тело, на которое действует какая-либо внеш­няя нагрузка, рассекается (мысленно) на две части плоскостью, про­ходящей через интересующую точку (рис. 2.1, а), в которой хотят определить напряжение. Затем отбрасывается (условно) одна из час­тей, например правая относительно плоскости. Действие отброшен­ной части тела на оставшуюся заменяется действием внутренних сил, которые сводятся к внешним силам.

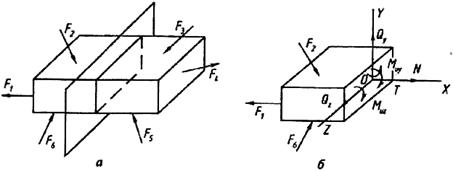
Рис. 2.1

Так как рассматриваемая часть тела свободна, не ограничена в движении связями и находится в состоянии покоя, к системе дейст­вующих на нее сил применимы условия равновесия. Для равновесия системы сил необходимо и достаточно, чтобы суммы проекций всех сил на координатные оси и суммы моментов всех сил относительно осей координат были равны нулю.

Со стороны отброшенной части тела на оставшуюся действуют распределенные по сечению внутренние силы. В общем случае сис­тему внутренних сил можно привести в точку к одной силе (главному вектору) и к одной паре сил (главному моменту). Вы­берем систему координат осей OX, OY, OZ c началом в центре масс се­чения (рис. 2.1,6). Ось ОХ направим по нормали к сечению, а оси OY и OZ расположим в его плоскости.

Составляющая внутренних сил, действующая вдоль нормали к сечению, называется нормальной силой в сечении. Она вызывает деформацию растяжения или сжатия. Со­ставляющие, действующие в плоскости сече­ния и стремящиеся сдвинуть одну часть тела относительно другой, называются поперечными силами. Момент внутренних сил 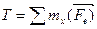, действующий в плоскости сечения, скручивает тело и называется кру­тящим моментом (T). Моменты 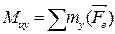и и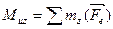згибают тело соответственно в плоскостях XOZ и XOY и называются изгибающими моментами. Определяют эти составляющие (рис. 2.1, б) через внешние силы.

Закон распределения внутренних сил по сечению можно охарак­теризовать с помощью напряжений, которые рассматривают как ко­личественную меру внутренних сил.

Рассмотрим сечение некоторого тела (рис. 2.2, а). В окрестности точки К выделим элементарную площадку 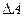, в пределах которой определена внутренняя сила 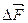. Отношение 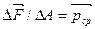называют средним напряжением на площадке 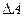. Уменьшая площадку, в пределе получаем полное напряжение в точке К по рассматриваемому сечению:

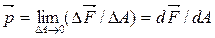
которое по наравлению совпадает с внутренними силами, имеет раз­мерность силы, распределенной по площади, и измеряется в паска­лях, мегопаскалях.

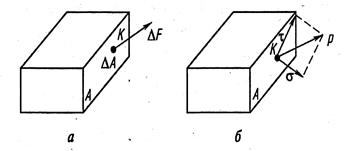
Рис. 2.2

Разложим вектор 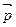полного напряжения (рис. 2.2, б) на две со­ставляющие: по нормали к плоскости сечения и в плоскости сечения. Составляющая полного напряжения, направленная по нормали к плос­кости сечения, называется нормальным напряжением и обозначается σ. Составляющую полного напряжения, лежащую в плоскости сече­ния, называют касательным напряжением и обозначают τ.

Различать нормальные и касательные напряжения необходимо, так как конструкционные материалы по-разному сопротивляются их действию (разные значения допускаемых напряжений, модуля упру­гости и т.д.).

Совокупность напряжений, возникающих в множестве сечений (площадок), проходящих через рассматриваемую точку, называется напряженным состоянием в точке. Напряженное состояние можно охарактеризовать, зная напряжения на любых трех взаимно перпен­дикулярных площадках, проходящих через эту точку.

2.2 Простейшие типы деформации стержней

В зависимости от геометрических признаков конструкции, осо­бенностей формы детали механизмов и машин можно разбить на элементы типа стержней, пластин и оболочек. К стержням относят тела, длина которых значительно больше линейных размеров поперечного сече­ния, а к пластинам — тела (например, мембраны), линейные размеры которых вдоль одной координатной оси намного меньше размеров вдоль остальных осей. Тела с размерами, соизмеримыми вдоль всех координатных осей (корпуса), относят к оболочкам. Большинство де­талей механизмов можно отнести к телам типа стержней. Это валы, оси, пружины, болты, штифты, шпонки, заклепки и другие элементы конструкций. В дальнейшем будем изучать поведение нагруженных внешними силами стержней, закономерности распределений напря­жений и деформаций в сечениях с наибольшей интенсивностью внут­ренних сил, т.е. в их поперечных сечениях.

В зависимости от схемы приложения внешних нагрузок или от вида составляющих внутренних сил, действующих в поперечных се­чениях стержней, различают следующие простейшие типы их дефор­маций: растяжение, сжатие, сдвиг, кручение и изгиб.

При растяжении или сжатии к концам стержня приложены силы, направ­ленные вдоль его оси. Они пытаются соответственно увеличить или уменьшить длину стержня. Иногда растяжение (сжатие) называют осевым или центральным.

При сдвиге силы направлены по нормали к продольной оси на очень близком друг от друга расстоянии и пытаются сдвинуть в плоскости поперечного сечения одну часть стержня относительно другой.

При кручении в торцовых сечениях стержня действуют противо­положно направленные моменты внешних сил, а при изгибе нагрузки должны действовать в плоскости, проходящей через продольную ось стержня.

Часто детали могут испытывать одновременно несколько дефор­маций, например валы одновременно подвергаются изгибу и круче­нию. Такое нагружение называется сложным сопротивлением.

2.3 Допущения, принимаемые при расчетах на прочность

Из-за сложности расчетов звеньев на прочность принимаются некоторые упрощающие расчет допущения относительно свойств ма­териалов и характера взаимодействия звеньев и нагрузок. Экспери­ментальная проверка расчетных зависимостей, полученных с учетом принимаемых допущений, показала возможность их использования для практических расчетов.

Детали механизмов перестают выполнять свои функции не толь­ко при разрушении, но и при изменении размеров, формы, т.е. при­обретая заметные остаточные деформации. Поэтому определение на­пряжений и деформаций проводят в области упругих деформаций, считая, что материал деталей обладает способностью полностью вос­станавливать первоначальные форму и размеры тела после устране­ния причин, вызвавших его деформацию, т.е. обладает свойством идеальной упругости.

Материал деталей является однородным и сплошным, т.е. свойства материала не зависят от размера и формы детали и оди­наковы во всех ее точках, будь это композиционный материал, пласт­масса или сплав.

Материал детали изотропен, т.е. обладает во всех направле­ниях одинаковыми свойствами. Различие свойств в разных направле­ниях (анизотропия) учитывают при расчете деревянных деталей.

В теле до приложения нагрузки нет начальных внутрен­них сил, т.е. отсутствуют напряжения.

Деформации тела очень малы по сравнению с его размерами и не влияют на взаимное расположение нагрузок.

Деформации материала в каждой его точке прямо про­порциональны напряжениям в этой точке (закон Гука).

Принцип независимости действия сил (принцип наложения): ре­зультат воздействия на тело системы сил равен сумме результатов воз­действия этих же сил, прилагаемых к телу отдельно в любом порядке.

Гипотеза плоских сечений (гипотеза Бернулли): поперечные сече­ния стержней, плоские до приложения нагрузки, остаются плоскими и нормальными к продольной оси стержня при действии нагрузки.