Ортогональное проецирование

При вспомогательном ортогональном про­ецировании вводится одна или большее число дополнительных плоскостей проекций. Каждая из них должна быть перпенди­кулярна к одной из данных или к вновь введенной и располагаться так, чтобы интересующая нас фигура (прямая, плоскость и др.) занимала по отношению к ней частное положение.

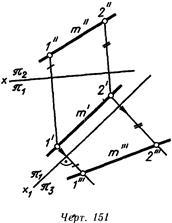
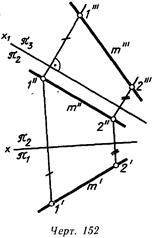
1. Прямая линия общего положения от­носительно плоскостей окажется в новой системе плоскостей проекций линией уровня, если новая плоскость проекций лз будет располагаться параллель­но ей (черт. 151 и 152).

На черт. 151 введена дополнительная плоскость лз параллельная прямой т и перпендикулярная к плоскости и с помощью точек / и 2 построе­на третья проекция прямой т — линия т'". Легко видеть, что в образовавшейся систе­ме плоскостей проекций ж/яз прямая т является линией уровня.

На черт. 152 дополнительная плоскость яз параллельна прямой - т и перпендику­лярна к плоскости . Теперь прямая т является линией уровня в систе­ме V/W.

Дополнительная плоскость проекций мо­жет быть расположена не только парал­лельно данной прямой, но и проходить через нее (черт. 153).

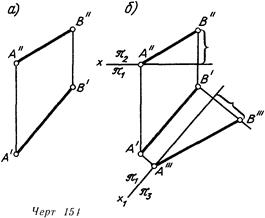
В случае, если ось проекции х в система , плоскостей проекций H/V. не зафиксирована (черт 154, а) для построения третьей проекции данной фигуры ее следует задать Ось можно провести произвольно (конеч­но, перпендикулярно к линии проекционной связи), но желательно, чтобы она была между данными проекциями объекта (см черт 151—153) .

Для того чтобы прямая линия была проецирующей прямой (т е проецировалась бы на какую либо плоскость точкой), должна быть плоскость проекций, перпендикулярная к ней

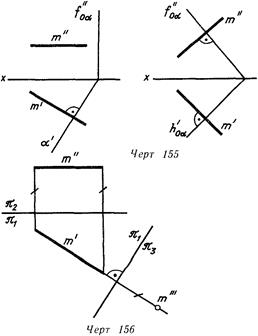
Плоскость проекций, перпендикулярная к одной из данных , может быть перпендикулярна только к пря мой частного положения (плоскость, перпендикулярная к прямой общего положения, является плоскостью общего положения, черт 155).

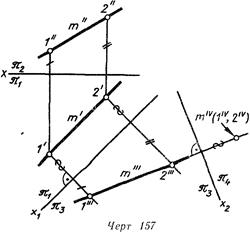
Для прямой же общего положения требуется введение двух дополнительных плоскостей проекций На черт 157 прямая т спроецирована с помощью точек / и 2 нa параллельную ей плоскость. В системе плоскостей она является уже линией уровня. Затем введена четвер­тая плоскость проекций . В систе­ме плоскостей проекций прямая является проецирующей и четвертое ее изображение представляет собой точку.

Итак, чтобы прямая общего положения оказалась на чертеже в новой системе плоскостей проекций проецирующей, необ­ходимо ввести две дополнительные плоскос­ти проекций: 3, параллельную прямой, и 4, перпендикулярную ей.

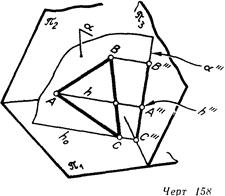
3. Плоскость общего положения относи­тельно плоскостей H и V окажется в новой системе плоскостей проекций, проецирую­щей, если новая плоскость проекций будет располагаться ' перпендикулярно к ней (черт. 158). Плоскость 3 будет перпенди­кулярна к плоскости а в том случае, когда она перпендикулярна к какой-нибудь линии этой плоскости. Прямая общего положения, лежащая в плоскости а, не может быть такой линией, так как тогда и плоскость 3 будет плоскостью общего положения (см. черт 155). Но плоскость 3 должна быть перпендикулярна либо плоскости H, либо плоскости V. Поэтому плоскость 3 должна быть перпендикулярна либо к гори­зонтали, либо к фронтали плоскости а.

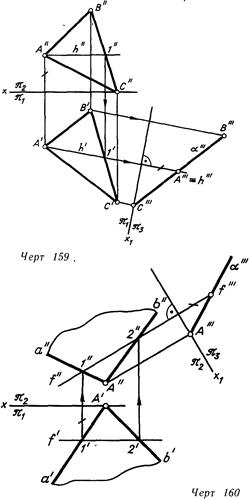
На черт. 158 и 159 введена дополни­тельная плоскость яз, перпендикулярная к горизонтали h плоскости а (ЛВС) и к пло­скости H|, и с помощью точек А и В построе­на проекция плоскости а — прямая а'"'. Очевидно, в образовавшейся системе пло­скостей проекций H/W плоскость а являет­ся проецирующей.

На черт. 160 введена плоскость проекций , перпендикулярная к фронтали данной плоскости а(а("|&), которая становится по­этому проецирующей в системе . В этом примере линия а'" найдена с помощью точек A и l.

Заметим, что в первом случае горизон­таль h, а во втором фронталь / проецируют­ся на плоскости 3 в виде точек.

В случаях, когда данные плоскости оп­ределены следами, плоскость 3 проводится перпендикулярно к одному из следов.

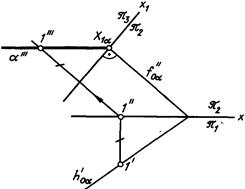
На черт. 161 проекция а.'" плоскости а определена точкой схода следов Xia и точкой /, взятой на ее горизон­тальном следе.

4. Для того чтобы данная плоскость ока­залась плоскостью уровня, необходимо ввести параллельную ей плоскость проекций

(плоскостью уровня называют плоскость, параллельную плоскости проекций). Оче­видно, этого нельзя сделать сразу при дан­ной плоскости общего положения, но воз­можно для проецирующей плоскости.

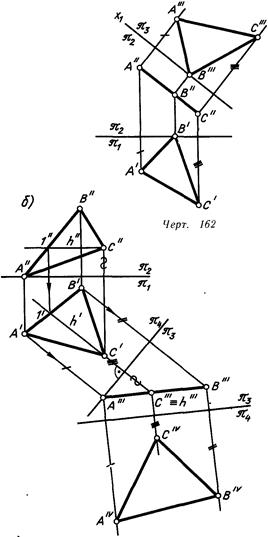
На черт. 162 задана фронтально проеци­рующая плоскость а (ЛВС) и введена допол­нительная, параллельная ей, плоскость проекций лз. В образовавшейся системе плоскостей проекций V/W плоскость а является плоскостью уровня.

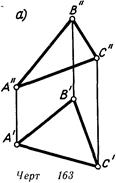
Чтобы плоскость общего положения ока­залась плоскостью уровня, требуется сна­чала ввести такую плоскость проекций Л3, чтобы образовалась система, в которой плоскость а будет проецирующей. Затем вводится дополнительная плоскость Л4, перпендикулярная к плоскости лз и парал­лельная плоскости а. На черт. 163, а показана заданная плоскость а, а на чер­теже 163, б выполнены указанные пре­образования.

ВЗАИМНОЕ ПОЛОЖЕНИЕ прямой ЛИНИИ, ПЛОСКОСТИ И КРИВЫХ ПОВЕРХНОСТЕЙ

ВЗАИМНОЕ ПОЛОЖЕНИЕ КРИВОЙ ПОВЕРХНОСТИ И ПЛОСКОСТИ

Плоскость может пересекать кривую поверхность (в частном случае — касается ее) При этом она имеет с поверхностью общую линию — линию пересечения поверх­ностей, представляющую собой в общем случае кривую линию

Если плоскость не имеет общих точек с кривой поверхностью, то говорят, что она не пересекает данной кривой поверхности

(В этом случае считают линию пересече­ния поверхностей мнимой )

Из чертежа взаимное положение пло­скости и кривой поверхности очевидно только в некоторых частных случаях, например, когда одна из этих поверхностей является проецирующей

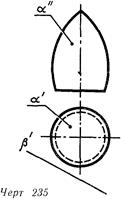
На черт 235 ясно, что поверхность тора а не пересекается с плоскостью р

На черт 236 цилиндрическая поверх­ность а пересекается с плоскостью |3 При этом линия пересечения поверхностей проецируется на горизонтальную плоскость окружностью, совпадающей с той, в которую проецируется поверхность цилиндра (а') Фронтальные проекции точек кривой опре­деляются с помощью линий плоскости р, проходящих через эти точки. Например, точка М" построена с помощью фронтали f .Фронтальные проекции точек соединены с помощью лекал

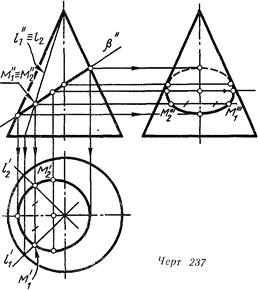
На черт.237 коническая поверхность а пересечена фронтально проецирующей пло­скостью ft Фронтальная проекция линии пересечения совпадает с проекцией плоскости т"==у Горизонтальная проекция строится по точкам, каждая из которых

определяется с помощью образующей, на которой она находится .

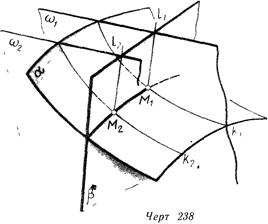
В общем случае для определения линии 'пересечения кривой поверхности с плоскостью применяют метод вспомогательных секущих плоскостей. Проводится ряд (семейство) секущих плоскостей. Каж­дая из них пересекает кривую поверхность а по линии k, a плоскость р — по прямой линии / (черт 238).

Определяются точки пересечения соответствующих пар линий (если никакие пары линий не пересекаются, то и поверхности а и р не имеют общих точек, т. е. не пересекаются). Линия пересечения поверхностей проходит через полученные точки..

Две плоскости пересекаются по прямой линии. Поверхность 2-го порядка пересекается плоскостью по кривой 2-го порядка Поверхность 4-го порядка (поверхность то­ра) пересекается плоскостью по линии 4-го порядка и т. д.

Заметим еще, что параллельные плоскос­ти пересекают поверхности 2-го порядка по подобным кривым.

Конические сечения

Коническими сечениями называют линии, получающиеся в результате пересечения конической поверхности 2-го порядка (в частном случае конической поверхности вра­щения) плоскостью.

Заданная на черт. 239, а фронтально проецирующая плоскость р пересекает коническую поверхность вращения а по эл­липсу (см. также черт 237).

Действительно, кривая 2-го порядка, по­лучающаяся при этом, не имеет несоб­ственных точек, так как все образующие поверхности а пересекаются с плоскостью Р (что очевидно из чертежа). В результате пересечения поверхности а с плоскостью у, перпендикулярной к оси вращения поверх­ности, получается окружность—част­ный вид эллипса.

На черт. 239, б фронтально проецирую­щая плоскость р параллельна левой очер­ковой образующей конуса Со всеми осталь­ными образующими поверхности а эта плоскость пересекается (с некоторыми за пределами чертежа). В сечении получается кривая 2-го порядка, имеющая одну несобственную точку е. парабола, т.

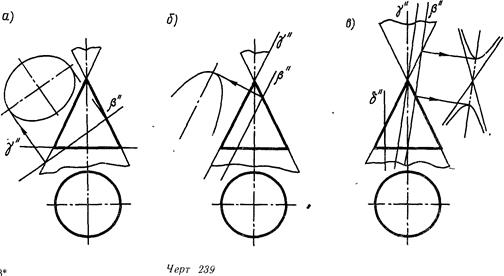
Плоскость -у касается поверхности конуса Касание происходит по образующей, кото­рую можно рассматривать как пару парал­лельных совпадающих прямых. Пара парал­лельных прямых является частным видом параболы.

На черт. 239, в плоскость р параллельна двум образующим конуса, расположенным в плоскости у. Остальные образующие его пересекаются с плоскостью (3, причем, неко­торые в точках, расположенных выше вер­шины конуса, т. е. на верхней его поле. Кривая 2-го порядка, получающаяся в этом случае, имеет две несобственные точки и является поэтому гиперболой. Легко видеть, что эта кривая имеет две части (ветви), одна из которых расположена на нижней части конической поверхности, дру­гая — на верхней. Плоскость "у, проходящая через вершину конуса, пересекает поверх­ность по паре образующих, являю­щихся частным видом гиперболы

Плоскость 6,параллельная оси конуса, а следовательно, и двум образующим по­верхности, пересекает коническую поверх­ность тоже по гиперболе.