Ортогональное дополнение. Ортогональная проекция и составляющая.
Пусть V – евклидово пространство со скалярным произведением (x,y), W – подпространство V.
Множество всех векторов x, ортогональных всем векторам из W, которое обозначим 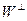 , называется ортогональным дополнением к подпространству W. Опишем свойства ортогонального дополнения.
, называется ортогональным дополнением к подпространству W. Опишем свойства ортогонального дополнения.
Свойство 2.3. 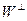 - линейное подпространство V.
- линейное подпространство V.
Доказательство. Пусть 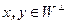 , тогда
, тогда 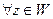 справедливы равенства
справедливы равенства 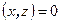 и
и 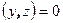 . Из этих равенств выводим равенства
. Из этих равенств выводим равенства 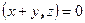 и
и 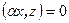 , то есть
, то есть 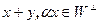 . Тем самым свойство доказано.
. Тем самым свойство доказано.
Свойство 2.4 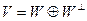 .
.
Доказательство. Построим ортогональный базис 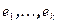 подпространства W и дополним его до ортогонального базиса
подпространства W и дополним его до ортогонального базиса 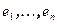 всего пространства V. Векторы
всего пространства V. Векторы 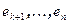 ортогональны векторам
ортогональны векторам 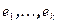 , а, значит и любому вектору из W. Следовательно, векторы
, а, значит и любому вектору из W. Следовательно, векторы 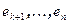 принадлежат ортогональному дополнению к W. Разложим произвольный вектор x по базису
принадлежат ортогональному дополнению к W. Разложим произвольный вектор x по базису 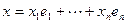 и положим
и положим 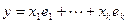 ,
, 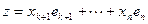 . Поскольку x=y+z и
. Поскольку x=y+z и 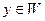 ,
, 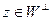 , то установлено равенство
, то установлено равенство 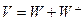 .
.
Покажем, что сумма прямая. Пусть 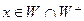 , тогда (x,x)=0 как скалярное произведение вектора из W на вектор из ортогонального дополнения к W. Единственный вектор нулевой длины равен 0, и, значит, пересечение содержит только нулевой вектор и сумма прямая.
, тогда (x,x)=0 как скалярное произведение вектора из W на вектор из ортогонального дополнения к W. Единственный вектор нулевой длины равен 0, и, значит, пересечение содержит только нулевой вектор и сумма прямая.
Следствие 2.4 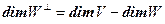 .
.
Доказательство вытекает из свойства прямой суммы подпространств.
Любой вектор x пространства V можно представить в виде суммы вектора y из подпространства W и вектора z из 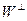 , причем векторы y и z определяются единственным образом. Вектор y называется ортогональной проекцией x на W и обозначается
, причем векторы y и z определяются единственным образом. Вектор y называется ортогональной проекцией x на W и обозначается 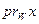 , а вектор z – ортогональной составляющей вектора x и обозначается
, а вектор z – ортогональной составляющей вектора x и обозначается 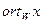 . О способах построения ортогональной проекции и ортогональной составляющей будет разговор в п.2.6.
. О способах построения ортогональной проекции и ортогональной составляющей будет разговор в п.2.6.
Свойство 2.5. 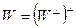 .
.
Доказательство. Применив Следствие 2.4, получим 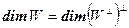 . Пусть x – произвольный вектор из W. Поскольку для произвольного вектора
. Пусть x – произвольный вектор из W. Поскольку для произвольного вектора 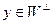 скалярное произведение (x,y)=0, то
скалярное произведение (x,y)=0, то 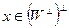 . Тем самым показано включение
. Тем самым показано включение 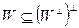 , из которого, в силу совпадения размерностей, выводим равенство
, из которого, в силу совпадения размерностей, выводим равенство 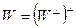 .
.
Пусть 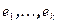 базис W. Вектор z принадлежит ортогональному дополнению к W тогда и только тогда, когда
базис W. Вектор z принадлежит ортогональному дополнению к W тогда и только тогда, когда 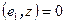 ,
, 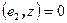 , …,
, …, 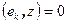 . Пусть
. Пусть 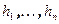 базис пространства V. В координатах, эти равенства превращаются в систему линейных уравнений
базис пространства V. В координатах, эти равенства превращаются в систему линейных уравнений 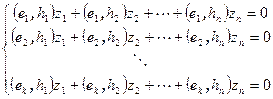 . Взяв в качестве W ортогональное дополнение к нему, получим следующее утверждение.
. Взяв в качестве W ортогональное дополнение к нему, получим следующее утверждение.
Свойство 2.6. Любое подпространство может быть задано системой линейных однородных уравнений.
В случае, если базис 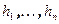 ортонормированный, коэффициентами при неизвестных в системе линейных уравнений являются координаты базисных векторов ортогонального дополнения.
ортонормированный, коэффициентами при неизвестных в системе линейных уравнений являются координаты базисных векторов ортогонального дополнения.
Дата добавления: 2016-07-27; просмотров: 2462;











