ОБЩИЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
При построении эпюра предмета* последний обычно располагают так, чтобы направления трех главных измерений его были параллельны плоскостям проекций (черт. 349): направление длины — параллельно оси х, ширины — оси у и высоты — оси z. Тогда длина и высота проецируются в натуральную величину на фронтальную плоскость проекций, длина и ширина не искажаются на горизонтальной проекции, а ширина и высота — на профильной. Такой чертеж нетрудно строить, по , нему просто производить измерения, судить о размерах изображенного, предмета. Однако он недос1аточно нагляден. На каждой из проекций отсутствует одно из трех измерений. Чтобы воспроизвести форму предмета, надо мысленно воссоздать ее по двум, трем, а иногда и большему числу проекций.
Более наглядный чертеж можно получить, проецируя предмет на одну плоскость проекций и располагая его так, чтобы ни одно из направлений главных измерений не проецировалось точкой.
На черт. 350 изображен такой же параллелепипед, как и на черт. 349, однако длина, ширина и высота его воспринимаются по одной проекции, так как взгляд «охватывает» сразу три стороны предмета По такому чертежу легко представить себе его форму.
Но второй чертеж обладает двумя существенными недостатками: во-первых, он необратим, так как представлена только одна проекция предмета; во-вторых, по чертежу нельзя произвести измерения предмета.
Чтобы ликвидировать первый "недостаток, чертеж дополняют второй проекцией, называемой вторичной.
Чтобы чертеж стал измеримым, на нем строят изображение системы координат Oxyz, оси которой параллельны соответственно
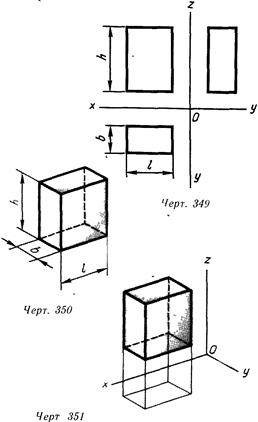
направлениям длины, ширины и высоты изображаемого предмета (черт. 351). Если известно, как искажаются размеры по осям х, у и z, то по чертежу можно судить о размерах предмета. Построенный таким образом чертеж называют аксонометрическим или аксонометрией.
Аксонометрические оси и показатели искажения. Для построения аксонометрических чертежей необходимо знать, как проецируются оси системы координат хугО (т. е. три взаимно перпендикулярные линии, проходящие через одну точку) и единичные отрезки, взятые на них.
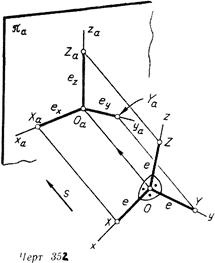
Рассмотрим черт. 352. Координатные оси системы Oxyz и отрезки на них [Х—0], [У—О] и [Z—0], равные натуральной единице е, спроецированы по направлению s на плоскость проекций Ла. В результате получены аксонометрические оси Xa. ya, Za, On и аксонометрические единицы вг, ёу, вг (в дальнейшем индекс «а» у аксонометрических проекций опускается).
Отношения
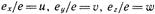
называют показателями искажения соответственно по осям Xa, Уа и Z„ аксонометрии. Показатели искажения связаны соотношением
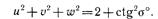
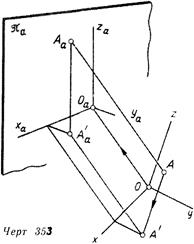
Вторичные проекции. Для получения второй проекции на плоскости Ла изображаемый объект предварительно проецируют на одну из координатных плоскостей. Затем полученную проекцию (вместе с осями координат) проецируют на плоскость Ли. Сказанное поясняет черт. 353. Точка А (объект) спроецирована сначала на плоскость хОу. Полученную проекцию А' проецируют затем на плоскость Л.. В конечном результате на аксонометрическом чертеже получаются два изображения точки А: Аа и А'а (вторичная), которые вполне определяют ее положение относительно системы координат Oxyz.
Виды аксонометрических проекций. Аксонометрическая проекция называется косоугольной, если направление проецирования s не перпендикулярно к плоскости проекций (о=т'=90°).
Аксонометрическая проекция называется прямоугольной, если направление проецирования s перпендикулярно к плоскости Ла(о=90°).
Кроме того, различают:
1. Триметрические проекции. Все показатели искажения здесь различны
2. Диметрические проекции Два показателя искажения равны, третий — не равен им. При этом возможны три случая: a) u=v^=w, б) и=/=и=гр и в) u=^-v^=w=u..
1. Изометрические проекции. Все показатели равны:
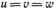
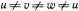
Дата добавления: 2017-02-13; просмотров: 1553;











