ПЕРЕСЕЧЕНИЕ ПРЯМОЙ ЛИНИИ С ПЛОСКОСТЬЮ

Точка пересечения прямой линии и плос­кости определяется на чертеже также с помощью секущей плоскости. Искомая точка М должна находиться на данной прямой т и в данной плоскости а, т. е. лежать на какой-либо линии / плоскости а (черт. 141). Прямую / получают сече­нием данной плоскости а вспомогательной плоскостью о), проходящей через прямую т. Тогда линии т и / пересекаются и образуют искомую точку М. Ход решения задачи:

1. Через прямую проводят некото­рую секущую плоскость .

2. Строят линию пересечения этой плоскости с заданной плоскостью

3. Определяют точку пересечения пря­мых т и I, являющуюся искомой: т{\1=М.

Из бесчисленного множества плоско­стей, которые можно провести через прямую т, выбирается такая, которая пересека­ется с плоскостью а по линии, легко опре­деляемой на чертеже. Обычно используют проецирующие плоскости, линии пересече­ния которых с плоскостью а. очевидны

На черт. 142 плоскость а задана пере­секающимися прямыми а и Ь. Через пря­мую т проведена фронтально проецирую­щая плоскость. Построена линия / пересечения плоскостей w и а. Фронтальная проекция ее совпадает с изображением плоскости -гори­зонтальная построена с помощью точек / и 2, лежащих на прямых а и Ь. Опре­делена точка пересечения М прямых т и /. Горизонтальная проекция этой точки полу­чена в пересечении л1тний т' и /', фрон­тальная определена с помощью линии проекционной связи М'—М"

Для определения видимости прямой линии т относительно плоскости а рас­смотрены конкурирующие точки 1 к 3. Их фронтальные проекции совпадают, а горизонтальные показывают, что точка /, при­надлежащая плоскости а, находится даль­ше точки 3, принадлежащей прямой от. Из этого следует, что на фронтальной проек­ции прямая слева от точки М видна, так как находится перед плоскостью. Пра­вая часть прямой находится за плос­костью. Для определения видимости на горизонтальной проекции можно восполь­зоваться другой парой конкурирующих то­чек, либо, определив, что данная плос­кость а — «тупоугольная», заключить, что слева от точки М прямая т не видна, а справа — видна. (Видимость на фронталь­ной проекции обратна видимости на гори­зонтальной).

При определении видимости прямой линии относительно плоскости, заданной следами, можно руководствоваться еще тем, что след плоскости всегда находит­ся за (под) прямой линией, если последняя расположена в I четверти пространства.

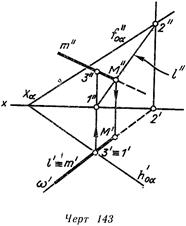
На черт. 143 плоскость а задана сле­дами. Через прямую линию от проведена горизонтально проецирующая плоскость w(w'=m'). Построена линия I пересе­чения плоскостей а и w. Горизонтальная проекция линии / совпадает с горизон­тальной проекцией плоскости w (l=w'), a фронтальная построена с помощью точек / и 2, лежащих соответственно на гори­зонтальном и фронтальном следах плоскости а.

Для определения видимости прямой относительно плоскости рассмотрены конку­рирующие точки 1 и 3. расположенные на горизонтальном следе и прямой т. Горизонтальные проекции точек совпадают, а фронтальная проекция точки 3 нахо­дится выше фронтальной проекции точки /. Следовательно, на горизонтальном изображении прямая m слева от точки М видна. Видимость на фронтальной проекции может быть определена также с помощью пары конкурирующих точек. ­

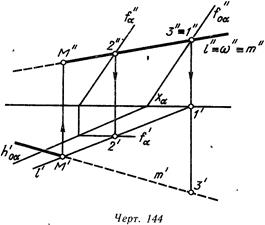
На черт. 144' приведен еще один пример построения точки пересечения пря­мой линии с плоскостью.

Через прямую от проведена фронтально проецирующая плоскость w (w'= m"). Линия пересечения l плоскостей а и w получена с помощью точки 1, лежа­щей на фронтальном следе плоскости и точки 2 пересечения плос­кости w с дополнительной фронталью f„ плоскости a. Точка М получена в пересечении линий mи l(l—2). На фрон­тальной проекции прямая от видна справа от точки М, так как она справа «перекры­вает» линию foa- На горизонтальной проек­ции по аналогичной причине прямая от видна слева от точки М.

СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА

Фигура, изображенная на чертеже, мо­жет быть так расположена относительно плоскостей проекций, что решение задач, связанных с нею или ее элементами (ли­ниями, поверхностями), может оказаться затрудненным. В предыдущих главах мы имели возможность убедиться в том, что построение изображений, а также опреде­ление по чертежу взаимного расположе­ния заданных геометрических элементов значительно проще при частном их располо­жении относительно плоскостей проекций. Поэтому необходимо уметь при отсутствии соответствующих условий искусственно со­здавать их на чертежах, т. е. произво­дить преобразование чертежа.

В первую очередь необходимо осуществ­лять:

1. Преобразование, при котором прямая линия общего положения становится прямой уровня.

2. Преобразование, при котором прямая линия общего положения или прямая уровня становится проецирующей прямой.

3. Преобразование, при котором пло­скость общего положения становится прое­цирующей плоскостью.

4. Преобразование, при котором пло­скость общего положения или проецирую­щая плоскость становится плоскостью уровня.