РАЗВЕРТЫВАНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ

<5 6 7 8910 11 >

Кривые поверхности, которые полностью, без растяжения или сжатия, без разрывов и складок можно совместить с плоскостью, называют развертываемыми. К этим поверхностям относятся лишь линейчатые и только такие, у которых смежные образующие пересекаются между собой или параллельны. Этим свойством обладают торсы (поверхности, образованные прямыми, касательными к направляющей пространственной кривой), конические и цилиндрические поверхности.

Остальные линейчатые поверхности, а также все нелинейчатые являются не развертываемыми.

Развертки развертываемых кривых поверхностей f

Цилиндрические поверхности в общем случае развертываются теми же способами, что и призматические. На черт. 342 способом «нормального сечения» построена развертка боковой поверхности наклонного цилиндра вращения. Для этого цилиндр пересечен плоскостью а, перпендикулярной к его образующим, которая делит поверхность цилиндра на две части

Нормальным сечением является окружность, проецирующаяся без искажения на вспомогательную плоскости яз. Разделив эту окружность, например, на восемь равных частей, проведем через точки деления образующие цилиндра, которые проецируются в натуральную величину на плоскость па- Взяв на горизонтальной прямой т отрезок, равный длине окружности нормального сечения, и разделив его на восемь равных частей, проведем через точки /о, 2о, За, ... деления прямые, перпендикулярные к линии т. На них вверх и вниз от линии т отложим длину соответствующих отрезков образующих цилиндра, которые берем с фронтальной проекции. Соединив концы

* При решении практических задач число делепий должно быть 12 — 16 и более построенных образующих плавной линией, получим развертку боковой поверхности цилиндра.

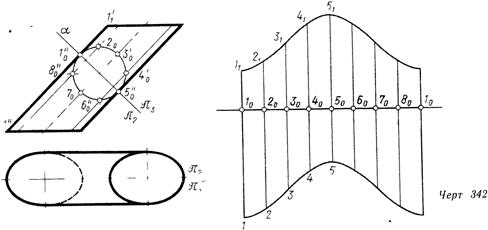
Поскольку количество точек для построения лекальных кривых определяется количеством частей, на которые делится нормальное сечение цилиндра, оно зависит от необходимой степени точности выполнения развертки. Отметим, не приводя доказательств, что кривые, ограничивающие построенную развертку, являются синусоидами.

Нижнее и верхнее основания цилиндра ограничены одинаковыми эллипсами, натуральный вид которых определяется их горизонтальными проекциями. Для получения полной развертки к изображенной на черт. 342 развертке боковой поверхности добавляют два основания цилиндра.

В рассмотренном примере, допуская некоторую ошибку, можно было бы откладывать на прямой т вместо длин дуг 'окружности длины стягивающих их хорд. При такой замене цилиндрическая поверхность была бы приближенно заменена поверхностью восьмигранной призмы.

Именно так было бы целесообразно поступить, если нормальным сечением была бы не окружность, а другая кривая (например, эллипс), которую трудно делить на равные части

Построение приближенной развертки боковой поверхности конуса дано на черт 343. Поверхность конуса заменена поверхностью вписанной в него пирамиды со стороной основания, равной хорде, полученной от деления окружности на восемь равных частей. Каждая грань пирамиды — треугольник. Одна сторона его равна

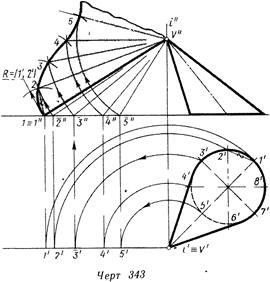
хорде, стягивающей 1/8 часть окружности основания конуса, а две другие стороны равны длинам соответствующих образующих конуса. Их натуральные величины определены способом вращения вокруг вертикальной оси I, проходящей через вершину конуса. Коническая поверхность рассечена по образующей V—/. После поворота до положения фронтали получена ее натуральная величина | V"—1"\ и от этой линии начато построение развертки. Последовательно найдены точки 2, 3, 4, .., которые затем соединены плавной лекальной кривой.

Развертка боковой поверхности прямого кругового цилиндра радиуса R и высотой h (черт. 344) представляет собой прямоугольник, одна из сторон которого

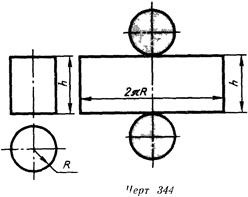
равна длине 2nR окружности основания а другая — высоте А цилиндра

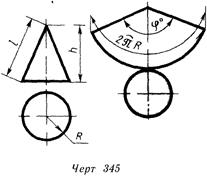
Развертка поверхности конуса вращения (черт 345) с радиусом основания R и высотой h представляет собой круговой сектор, радиус которого равен длине / образующей конуса, а центральный угол ц°=2пР/1

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

<5 6 7 8910 11 >

Дата добавления: 2017-02-13; просмотров: 3437;