ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
Центральное проецирование является наиболее общим случаем получения проекций геометрических фигур.
Сущность метода:
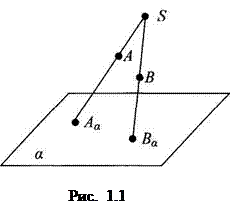 Дано: плоскость α;
Дано: плоскость α;
точка S, не принадлежащая плоскости α.
Возьмем произвольную точку А, не принадлежащую плоскости α (рис. 1.1). Проведем луч SA. SA  α = Аα. Аналогично, выбрав произвольную точку В и построив луч SВ, получим Вα.
α = Аα. Аналогично, выбрав произвольную точку В и построив луч SВ, получим Вα.
Здесь: α- плоскость проекций;
S - центр проекций;
SA, SВ – проецирующие лучи;
Аα, Вα - центральные проекции точек А и В
на плоскость α.
Аппарат центрального проецирования: плоскость α, точка S.
Утверждение: любой точке соответствует одна и только одна центральная проекция. Обратное утверждение не имеет смысла.
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Параллельное проецирование- частный случай центрального проецирования, при котором центр проекций удален в бесконечность.
Сущность метода:
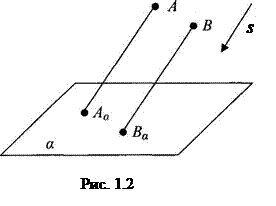
Дано: плоскость α,
точка S - бесконечно удалена от α.
Очевидно, что при таком положении центра проекций проецирующие лучи s будут параллельны друг другу (рис. 1.2).
Аппарат параллельного проецирования: плоскость проекций α, направление проецирования s.
Основные свойства параллельного проецирования:
1. Проекция точки есть точка.
2. Проекция прямой на плоскость есть прямая.
3. Если в пространстве точка принадлежит линии, то проекция этой точки принадлежит проекции линии.
4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
5. Точка пересечения проекций пересекающихся прямых является точкой пересечения этих прямых.
6. Плоская фигура, параллельная плоскости проекций, проецируется на эту плоскость в конгруэнтную фигуру.
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
8. Параллельный перенос оригинала или плоскости проекций не изменяет вида и размеров проекции оригинала.
Дата добавления: 2016-11-04; просмотров: 1489;











