ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ. ПРОЕЦИРОВАНИЕ ТОЧКИ

Любой предмет пространства может рассматриваться как определенная совокупность отдельных точек этого пространства. Поэтому для изображения различных предметов пространства необходимо научиться строить изображения отдельной точки пространства.

Таким образом, изучение метода построения ортогонального чертежа начнем с изучения проецирования точки.

Представим в пространстве три взаимно перпендикулярные плоскости (рис. 6, а):

p₁ - горизонтальную плоскость проекций;

p₂ - фронтальную плоскость проекций;

p₃ - профильную плоскость проекций.

Для наглядного изображения плоскостей проекций взята так называемая кабинетная проекция[1], известная из курсов геометрии и черчения средней школы.

Плоскости проекций пересекаются по прямым, которые называются осями проекций и обозначаются x, y и z. Точка О – точка пересечения всех трех осей проекций – называется началом координат.

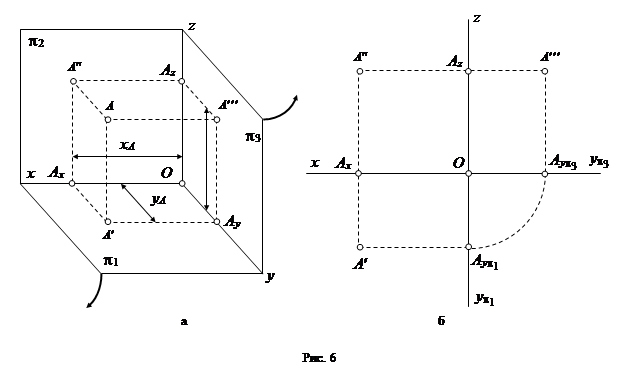
Представим себе также в пространстве некоторую точку А. Для того, чтобы получить проекцию точки A на горизонтальную плоскость проекций p₁, необходимо провести через эту точку прямую, перпендикулярную плоскости p₁, и найти точку пересечения A¢ этой прямой с плоскостью p₁. Точка A¢ называется горизонтальной проекцией точки A. Путем ортогонального проецирования точки A на фронтальную p₂ и профильную p₃ плоскости проекций образуются ее фронтальная и профильная проекции (соответственно точки A¢¢ и A¢¢¢).

Длины отрезков, измеряемые некоторой установленной единицей длины и равные расстояниям от точки А до горизонтальной p₁, фронтальной p₂ и профильной p₃ плоскостей проекций, называются прямоугольными (декартовыми) координатами:

- по оси x - абсцисса, равная отрезку x_A=|AA¢¢¢|;

- по оси y - ордината, равная отрезку y_A=|AA¢¢|;

- по оси z - аппликата, равная отрезку z_A=|AA¢|.