Форсирующее (пропорционально-дифференцирующее) звено

Уравнение форсирующего звена представляется в следующем виде:

y(t) = k(Tx′(t) + x(t))(1.104.)

где k - передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного в статическом режиме, T- постоянная (времени) инерционности звена, с ее увеличением возрастает время изменения величины выходного параметра, при изменении входного. При нулевых начальных условиях это уравнение принимает в операторной форме следующий вид:

Y(р) = k(TрX (р) + X (р)) (1.105.)

Передаточная функция форсирующего звена будет выглядеть, как:

W(p)= k (Tр + 1) (1.106.)

АФЧХ форсирующего звена выражается в виде:

W(jω) = Re(ω) + Im(ω) = k(T( jω) +1) = k + jkTω(1.107.)

определим АЧХ форсирующего звена:

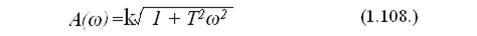
ФЧХ форсирующего звена будет выглядеть, как

j(w ) = arctg(kTω / k) = arctg Tω (1.109.)

Переходная функция форсирующего звена представлена в виде:

h(t) = k [T δ(t) +1(t)](1.110.)

Импульсная переходная характеристика имеет следующее значение:

w(t) = h′(t) = k[Tδ ′(t) +δ (t)] (1.111.)

Графическое изображение частотных характеристик форсирующего звена представлено на рисунке 41. Величина ω_сп определяется, как точка пересечения асимптот, и ее численное значение равно ω_сп = 1/ T. Анализируя ЛАЧХ И ЛФЧХ, можно заметить, что при увеличении частоты входных колебаний до частоты ω_сп, амплитуда выходных колебаний постоянна, а при увеличении частоты входных колебаний более ω_сп, амплитуда выходных колебаний начинает увеличиваться.

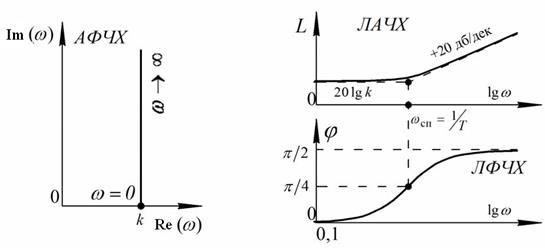
Рис.41. Графики частотных характеристик форсирующего звена

Следовательно, форсирующее звено усиливает высокие частоты.

Сдвиг по фазе между входными и выходными колебаниями положительный и стремится к значению π /2.

Рассмотренные выше типовые звенья систем автоматического управления являются минимально-фазовыми, кроме запаздывающего звена.

Минимально-фазовымназывается звено, у которого модуль сдвига по фазе при одинаковой частоте, минимален по сравнению с другим звеном, имеющим такую же АЧХ.

Если все нули и полюса передаточной функции рассматриваемого звена будут иметь равные нулю или отрицательные действительные части, то такое звено будет считаться минимально-фазовым.

Различают также неустойчивые звенья, особенность которых заключается в наличии больших по сравнению с устойчивыми звеньями сдвигов по фазе между входными и выходными колебаниями. Поэтому неустойчивые звенья можно отнести к неминимально-фазовым звеньям. К неминимально-фазовым звеньям можно также отнести звенья, которые имеют в числителе передаточной функции (в правой части дифференциального уравнения) вещественные положительные корни или комплексные корни с положительной вещественной частью. Например, звено с передаточной функцией, выраженной следующим образом, будет являться неминимально-фазовым:

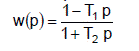(1.111.1.)

К неустойчивым звеньям также можно отнести звенья со следующими передаточными функциями:

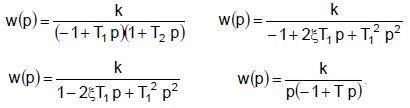(1.111.2.)

Применение в системах автоматического управления неустойчивых звеньев обуславливает некоторые особенности расчетов, не рассматриваемых в настоящей книге.

На рисунке 41.1. представлена таблица, в которой для лучшей наглядности обобщены значения передаточных функций типовых звеньев.

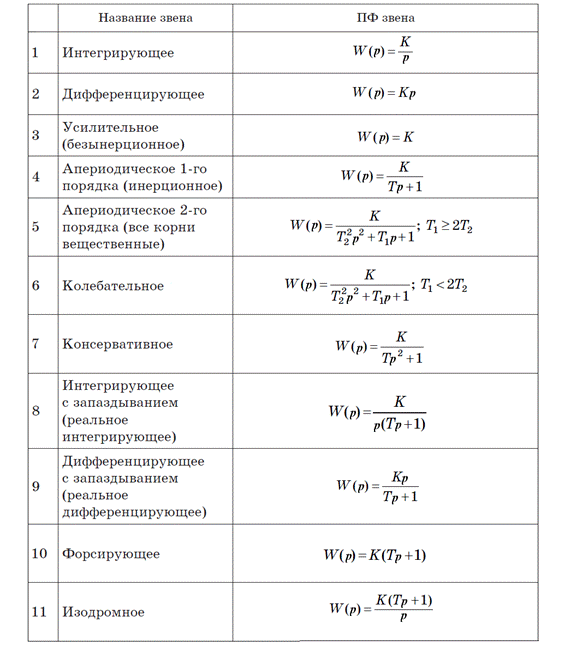
Рис.41.1. Передаточные функции типовых звеньев