Запаздывающее звено

Уравнение запаздывающего звена представляется в следующем виде:

y(t) = x(t - τ) (1.97.)

где τ- является временем запаздывания. При нулевых начальных условиях это уравнение принимает в операторной форме следующий вид:

Y (р) = X (р)℮^-pt (1.98.)

Передаточная функция запаздывающего звена будет выглядеть, как:

W(p)= ℮^-pt (1.99.)

АФЧХ запаздывающего звена выражается в виде:

W(jω) = Re(ω) + Im(ω) = A(ω)℮ ^jj(w)= cos ωτ - j sin ωτ (1.100.)

на основании данного выражения определим АЧХ и ФЧХ запаздывающего звена:

A(ω) = 1; j(w ) = arctg( - sin ωτ/ cos ωτ) = - ωτ(1.101.)

Переходная функция запаздывающего звена представлена в виде:

h(t) = 1(t − τ)(1.102.)

Импульсная переходная характеристика имеет следующее значение:

w(t) = h′(t) = δ (t −τ )(1.103.)

Графическое представление частотных характеристик запаздывающего звена представлено на рисунке 39.

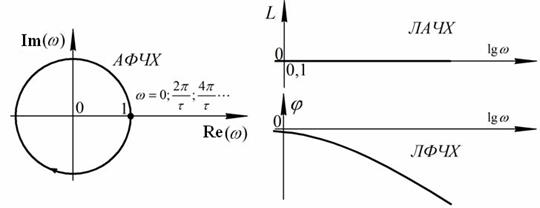
Рис.39. Графики частотных характеристик запаздывающего звена

Анализируя графики частотных характеристик можно отметить, что выходной сигнал отстает по фазе от входного, и отставание увеличивается с увеличением частоты. В то же время соотношение амплитуд сигналов от частоты не зависит.

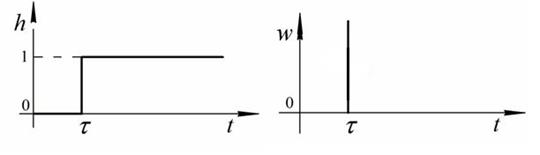
Рис.40. Графики временных характеристик запаздывающего звена

На практике запаздывающее звено ухудшает устойчивость реализуемой системы, при включении в систему данного звена ухудшается ее управляемость. Анализ и синтез таких систем затруднителен, поэтому на практике передаточную функцию запаздывающего звена заменяют при расчетах дробно-рациональными функциями.