Колебательное звено: передаточная функция, ЛАЧХ, демпфирование и характеристики
Подставив в уравнение (1.63.) значение b0 = 0, получим дифференциальное уравнение второго порядка (уравнение состояния) следующего вида:
a0 y′′( t) + a1 y′ (t) + a2 y (t) = b1 x (t)(1.89.)
Передаточная функция звена 2 порядка может быть найдена с помощью преобразования по Лапласу и будет иметь следующий вид:
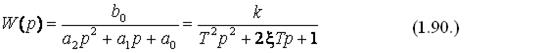
где k = b0/a0 – передаточный коэффициент звена, размерность которого определяется отношением размерности выходного параметра к размерности входного в статическом режиме, 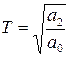 - постоянная (времени) инерционности звена, с ее увеличением возрастает время изменения величины выходного параметра, при изменении входного.
- постоянная (времени) инерционности звена, с ее увеличением возрастает время изменения величины выходного параметра, при изменении входного.  - коэффициент демпфирования (затухания), чем он больше, тем быстрее затухают колебания. Корни уравнения знаменателя из выражения (1.90.) характеризуют переходной процесс звена, приравняем уравнение к нулю:
- коэффициент демпфирования (затухания), чем он больше, тем быстрее затухают колебания. Корни уравнения знаменателя из выражения (1.90.) характеризуют переходной процесс звена, приравняем уравнение к нулю:
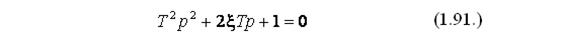
Так как pявляется комплексным числом, корни данного уравнения могут быть вещественными, мнимыми и комплексно-сопряженными. Для общего случая корни будут выглядеть, как:
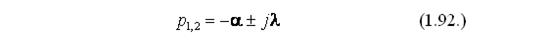
где 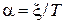 является постоянной времени затухания,
является постоянной времени затухания, 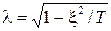 - собственная частота колебаний. Значением коэффициента x определяются динамические характеристики колебательного звена. Звено является колебательным только при
- собственная частота колебаний. Значением коэффициента x определяются динамические характеристики колебательного звена. Звено является колебательным только при
0 < x < 1, в этом случае, переходная функция имеет затухающий характер.
Передаточная функция колебательного звена в этом случае будет выглядеть:
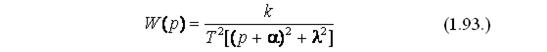
Переходную функцию получим, применив обратное преобразование Лапласа:
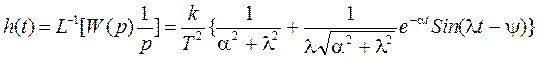 (1.94.)
(1.94.)
при этом 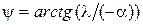 параметр начальной фазы переходного процесса.
параметр начальной фазы переходного процесса.
Графики временных характеристик колебательного звена представлены на рисунке 36.
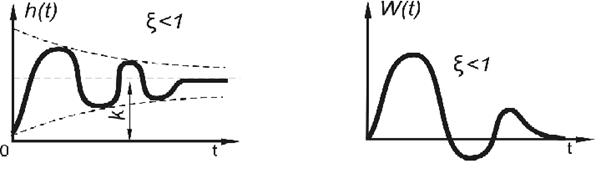
Рис. 36. Графики временных характеристик колебательного звена
При x = 0 колебательное звено называется консервативным, оно характеризуется незатухающими колебаниями на выходе. Консервативное звено представляет собой идеализированный генератор гармонических сигналов, работающий без потерь энергии.
Передаточная функция консервативного звена будет иметь вид:
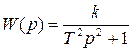 (1.95.)
(1.95.)
При x ≥ 1 колебательное звено представляет собой апериодическое звено 2 порядка.
Апериодическое звено 2 порядка можно рассматривать, как последовательное соединение апериодических звеньев 1 порядка, о которых упоминалось выше.
АФЧХ колебательного звена выражается в виде:
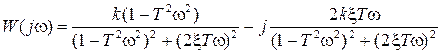 (1.96.)
(1.96.)
Действительная частотная характеристика звена Re(w) будет определяться первым слагаемым данного выражения, мнимая частотная характеристика Im(w) – вторым.
Графическое представление частотных характеристик колебательного звена представлено на рисунке 37.
Величина ωсп определяется, как точка пересечения асимптот, и ее численное значение равно ωсп = 1/ T.
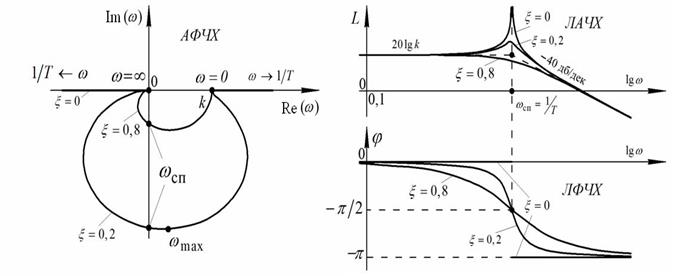
Рис. 37. Графики частотных характеристик колебательного звена
Анализируя ЛАЧХ И ЛФЧХ, можно заметить, что при увеличении частоты входных колебаний до частоты ωсп, амплитуда выходных колебаний постоянна, а при увеличении частоты входных колебаний более ωсп, амплитуда выходных колебаний начинает уменьшаться. Следовательно, колебательное звено фильтрует высокие частоты.
Сдвиг по фазе между входными и выходными параметрами колебаний отрицателен и с увеличением частоты стремится к значению –π.
С помощью степени затухания Ψ оценивают скорость затухания колебательного процесса, степень затухания представляют как:
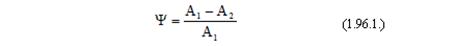
где А1и А2– соседние амплитуды.
Следовательно, чем ближе Ψ к единице, тем быстрее затухает колебательный процесс, а чем Ψ ближе к нулю, тем затухание колебательного процесса происходит медленнее. Величина Ψ зависит от соотношения вещественной α и мнимой β частей комплексных корней характеристического уравнения, поэтому может быть представлена в виде:
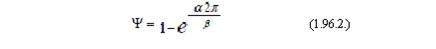
Степенью колебательности называют отношение мнимой части комплексного корня к вещественной части, выраженное как:
μ = β /α (1.96.3.)
с учетом этого (1.96.2.) примет вид:
Ψ =1−e−2π /μ(1.96.4.)
Коэффициент демпфирования (затухания) ξ связан со степенью колебательности μ следующим соотношением:
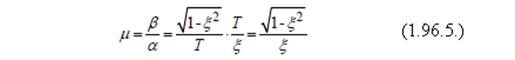
На рисунке 37.1 приведена таблица, в которой указана взаимосвязь между коэффициентами μ, Ψ и ξ .
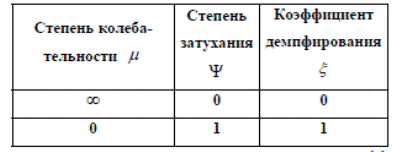
Рис. 37.1. Таблица взаимосвязи коэффициентов μ, Ψ и ξ
При анализе таблицы легко обнаруживается, что степень колебательности противоположна степени затухания и коэффициенту демпфирования (затухания). Чем больше μ, тем меньше Ψ и ξ, и наоборот.
Реализуемое на практике колебательное звено может представлять собой электрический колебательный контур с активным сопротивлением, изображенный на рисунке 38.
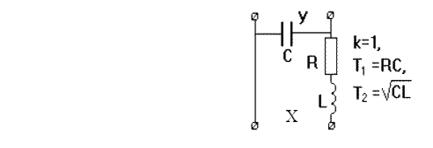
Рис. 38. Реальное представление колебательного звена
Дата добавления: 2017-01-26; просмотров: 5481;











